一类新的染色问题

韩淑芹

(青岛工学院 基础教育学院, 山东 胶州 266300)

1 主要结果

定理1 若G=L(H)且p≥4，则图G的全色极大团染色等价于图H的边覆盖染色.

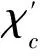
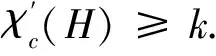
推论1 Gupta定理等价于下面两种情形

(1)若G=L(H)且p≥4，则p- 1≤χmaxcT(G)≤p.

(2)若G=T(H)且p≥4，则p- 1≤χmaxcT(G)≤p.

证明(1)可由定理1得出.

(2)将H的顶点染同种颜色，再由定理1可得结果.

定理2 若χmaxcT(G)=p，χmaxcT(H)=q,则χmaxcT(G[H])=pq.

证明由于E(G[H])={wijwkl∶uiuk∈E(G)或i=k,vjvl∈E(H)}，则G[H][5]的最小极大团点数为pq，故有χmaxcT(G[H])≤pq.下给出G[H]的一个pq-全色极大团染色.

令f:V(G)→{1,2,…，p},V(H)→{1,2,…,q},则f是图G,H的一个全色极大团染色.G中的点被分为p个子集，染有颜色i的点集记为Vi，1≤i≤p.令

f((ui,vj))=f(vj)+(i-1)q,

ui∈Vi,vj∈V(H).

G[H]的极大团形式为(ui,vj),(uk,vl),ui,uk∈G′,vj,vl∈H′,G′H′分别为G,H的极大团.显然G的每个极大团pq种颜色均出现，从而有χmaxcT(G[H])≥pq.

定理3 若p-1≤χmaxcT(G)≤p,q-1≤χmaxcT(H)≤q，则有

χmaxcT(G×H)=min{χmaxcT(G),χmaxcT(H)}.

证明由于E(G×H)={wijwkl,i=k和vjvl∈E(H)或j=l和uiuk∈E(G)}，则G,H的极大团仍为G×H[5]的极大团.不妨设χmaxcT(G)≤χmaxcT(H).

令f∶V(G)→{1,2,…，χmaxcT(G)},V(H)→{1,2,…，χmaxcT(H)},下对G×H的点进行染色.令f((ui,vj))=f(ui)⊕(j-1),ui∈V(G),vj∈V(H),⊕表示mod(χmaxcT(G))，其中(χmaxcT(G)-1)⊕1=χmaxcT(G).G×H的极大团有以下两种形式：

(1) (ui,vj),ui∈G′,G′为G的极大团，对某一固定的j,1≤j≤n,vj∈V(H).

(2) (uk,vl),vl∈H′,H′为H的极大团，对某一固定的i,1≤i≤m,ui∈V(G).

显然第(1)种形式的极大团χmaxcT(G)种颜色均出现，第(2)种形式的极大团χmaxcT(H)种颜色均出现.而χmaxcT(G)≤χmaxcT(H)，从而有χmaxcT(G×H)≥χmaxcT(G)

由于G×H的最小极大团为min{G′,H′}，故有χmaxcT(G×H)≤min{p,q}

(1)χmaxcT(G)=p,χmaxcT(H)=q. 结论显然成立.

(2)χmaxcT(G)=p-1,χmaxcT(H)=q.则有p-1≤q.

①p=q+1,有p-1≤χmaxcT(G×H)≤q=p-1. 结论成立

②p

同理可证χmaxcT(G)=p,χmaxcT(H)=q-1,χmaxcT(G)=p-1,χmaxcT(H)=q-1的情形.

2 待研究的问题

已经得到若G=L(H)或T(H)，有p-1≤χmaxcT(G)≤p.那么是否含全图或线图的图类中也有此结论？满足χmaxcT(G)=p的图类有哪些？另外可以定义全色最大匹配染色，全色极大星染色，全色最长路染色等.我们将进一步研究有此类条件限制的染色问题.

[1] Miao L Y,Liu G Z.Edge covering coloring and fractional edge covering coloring[J]. Journal of Systems Science and Complexity,2002,15(2):187-193.

[2] Miao L Y,Pang S Y.Classification of graphs on edge covering coloring[J].Journal of Math(PRC),2001,21(4):368-372.

[3] 王纪辉，刘桂真.图的边覆盖染色与分数边覆盖染色[J].山东大学学报：理学版，2005,40(3):1-4.

[4] Bondy J A,Murty U S R.Graph theory with applications[M].New York:Macmillan,1976.

[5] Klavzar S.Coloring graph products-A survey[J].Discrete Mathematics,1996,155: 135-145.