基于泰勒展开的结构响应面方法

郭 明， 柴 山, 刘金钊

(山东理工大学 交通与车辆工程学院， 山东 淄博 255091)

1 预备知识

结构优化设计问题的数学模型一般形式为

findX=[x1,x2,…，xn]T∈Rn

minf(X)=f(x1,x2,…,xn)

s.t.σil≤[σ]i

(i=1,2,…,n；l=1,2,…,N)

(1)

⋮

其中X为设计变量；f(X)为目标函数；σil及δlk分别为应力约束条件和位移约束条件.

在一个结构设计方案中,全部变量可分为三种类型,即设计变量、性能变量和中间变量.

1)设计变量是结构优化设计中的自变量，通常由设计者主动选择.

2)性能变量是结构的各种性态变量,例如应力、位移、自振频率等等,是设计变量的因变量,设计者不能直接选出所需要的性态变量,而只能靠结构分析来描述.

3)中间变量是由设计变量求性态变量运算中的一些量.例如单元的应力是一个性态变量,求应力时所需的内力就是一个中间变量.

一般说来，在结构优化设计数学模型中，目标函数是设计者关心的目标与设计变量相关的函数，而约束条件是对性能变量的某些限制，是性能变量的函数[1].在有限元方程中，刚度矩阵、质量矩阵、阻尼矩阵是设计变量的函数，而应力、位移这些性能变量是要通过求解有限元方程求得的，因而是设计变量的隐函数.一般的数学规划问题的目标函数和约束条件都是设计变量的显函数，结构优化设计数学模型中约束条件是设计变量的隐函数，这也是结构优化设计问题区别于一般的数学规划问题的一个重要特点，由于这一特点，大大增加了结构优化设计问题的复杂性，增加了求解难度.

要解决结构优化设计数学模型中约束条件是设计变量的隐函数的问题，就必须进行约束条件的显式化，响应面方法是最常用的显式化方法.响应面方法最初由Box和Wilson于1951年提出[2]，其基本思想是通过一系列确定性实验，用多项式函数来近似隐式极限状态函数.通过合理地选取试验点和迭代策略，来保证多项式函数能够逼近于真实的隐式极限状态函数.当系统变量和系统输出响应以某种隐含的方式存在时，RSM无疑提供了一种近似表达这种隐含关系的合适手段.RSM方法在统计数据处理、工业过程控制和可靠度分析等领域已为人们所熟知，近几年在结构优化中也逐步得到了广泛的应用.1995年，Myers和Montgomery对响应面的及其应用进行了全面的阐述，并把响应面方法定义为“一种用于开发、改进、优化的统计和数学方法”[3].如今，响应面方法广泛用于优化设计中，即通过合理的试验设计方法构建目标函数、约束函数和设计变量之间的近似函数[4].

由于传统的多项式基响应面是应用最小二乘法建立的逼近函数，在某些问题中其拟合精度偏低.本文在结合桁架结构优化设计问题，分析传统多项式响应面法及其拟合精度的基础上，提出了基于泰勒展开的响应面法，可以有效地提高在展开点附近响应面的拟合精度，这对于结构优化设计非常有利.

2 传统多项式基响应面方法及其拟合精度分析

2.1 传统多项式基响应面算法简介

常用的多项式基响应面法的形式有下面几种:

线性型

(2)

二次型

(3)

完整二次型(含交叉项)

(4)

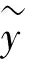
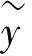
(5)

每次试验的表达式可统一写成如下矩阵形式

Y=Xβ+ε

(6)

其中

系数向量的无偏估计β可由最小二乘法获得，即令每次试验的误差平方和δ为最小

δ=εTε=(Y-Xβ)T(Y-Xβ)→min

(7)

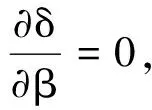
β=(XTX)-1XTY

(8)

2.2 多项式基响应面算法的精度分析

利用多项式基响应面方法进行显式化时，响应面的拟合的精度是要考虑的，文中用几个简单的算例对多项式基响应面方法的拟合精度进行探讨.本文主要讨论的是桁架结构，选取桁架结构的截面积为设计变量，截面积变化范围为0.01m2～0.05m2，且截面均为圆截面，弹性模量E=2.1×1011Pa，泊松比为0.3，以节点的位移为结构的响应.

算例1 以最简单的二杆桁架为例,二杆桁架结构如图1所示.

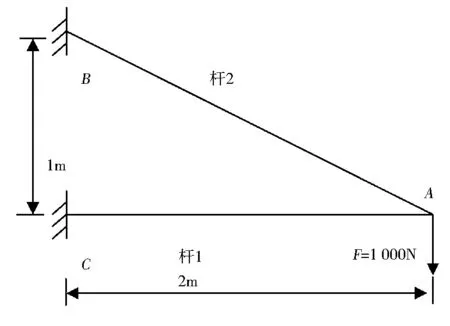
图1 二杆桁架结构

通过结构力学求得的二杆桁架的节点A沿力F方向的位移解析解如下：

利用多项式基响应面求解的A节点的近似响应值与真实响应值之间的相对误差和以及响应面形式的选择情况见表1.

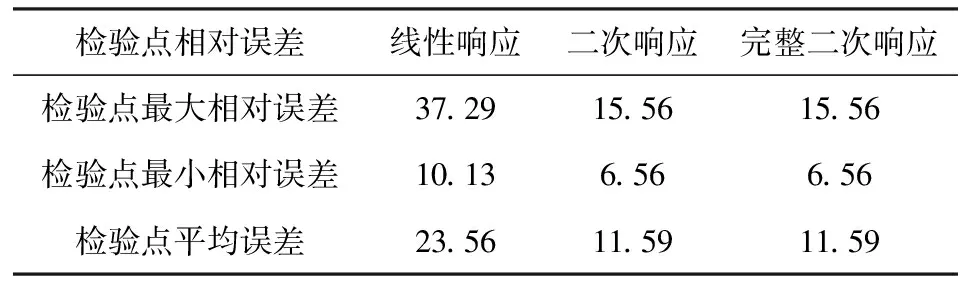
表1 二杆桁架的拟合精度及响应面形式的选择 %

算例2 分析一个超静定的六杆桁架的例子，六杆桁架的结构如图2所示[6].

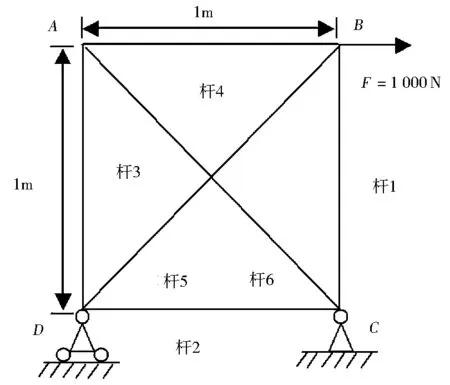
图2 六杆桁架结构

六杆桁架节点B沿力F方向的位移的解析解为

利用多项式基响应面求解B节点的近似响应值与真实响应值之间的相对误差和以及响应面形式的选择情况见表2.

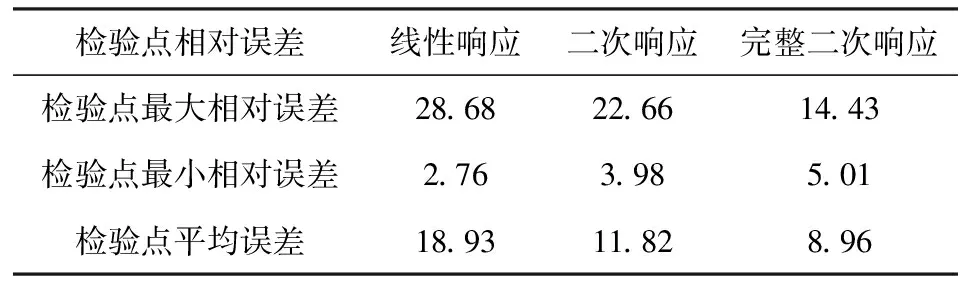
表2 六杆桁架的拟合精度及响应面形式的选择 %

由表1和表2可以看出，利用多项式基响应面方法对桁架结构的位移进行拟合时，线性形式的响应面在检验点处相对误都较大，不能够满足足够的逼近；二次形式的响应面在检验点处计算精度虽然有所提高，但是误差也很大；静定结构增加交叉项对拟合的结果影响很小，超静定结构增加交叉项后精度有所提高，但是也不能满足实际需求.

3 基于泰勒展开的响应面方法

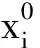
(9)

若线性形式的基于泰勒展开的响应面方程不能满足精度的要求，则可增加高阶形式的差分来进行补充构建响应面函数，根据工程经验和大量的资料分析可知，多元的二阶泰勒展开形式就能很好的满足实际需要，基于多元泰勒展开形式的二次响应面公式.

(10)

其中：若式(10)中不含混合的二阶偏导数，则称该展开为二次形式展开，若式(10)中含有混合的二阶偏导数，则称为完整二次形式展开.

写成矩阵形式为

S=S0+[S0]T(x-x0)+

其中H为海森矩阵

在差分网格图3中，Si,j，Si+1,j，…,Si-1,j-1,Si+1,j-1，分别表示节点(i,j)，(i+1,j)，…，(i-1,j-1)，(i+1,j-1)处性能函数S的响应值，若以节点(i,j)为展开点，则上述各式中偏导数的求解公式如下：

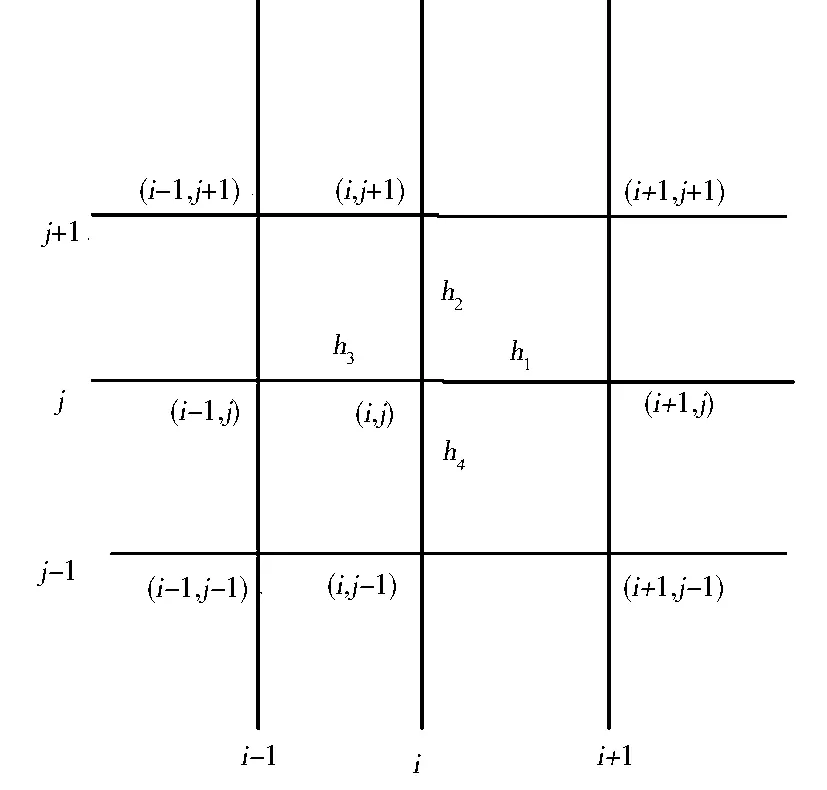
图3 差分的网格图

一阶偏导数：

(11)

二阶偏导数：

(12)

混合的二阶偏导数：

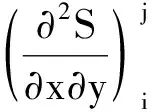
(Si+1,j+1+Si-1,j-1)]

(13)

对超静定结构利用基于泰勒展开的响应面进行分析时，超静定结构的响应S(内力、应力、位移、固有频率、振型以及失稳波形)等都是随设计变量X而变化的，是设计变量的函数[7].将S在X0处进行多元泰勒展开，得到型如式(10)形式的多元泰勒展开式.对于梁、杆、板、壳这类单元，其应力可由内力与截面几何性质的关系式求出，而截面几何性质就是设计变量，因此只要求得内力，就可以得到应力约束的显函数表达式.

4 算例验证

为了验证基于泰勒展开的响应面方法的求解精

度，这里主要分析第一节中介绍的算例.

4.1 二杆静定桁架

我们选择在设计变量的中心点处进行泰勒展开得到如式(10)形式的基于泰勒展开的显式化的响应面方程;对构建的响应面方程进行精度检验时，选择在各设计变量的相邻节点附近进行精度的验算，利用基于泰勒展开的响应面法求解的结果与通过结构的解析解求得结果的相对误差见表3.

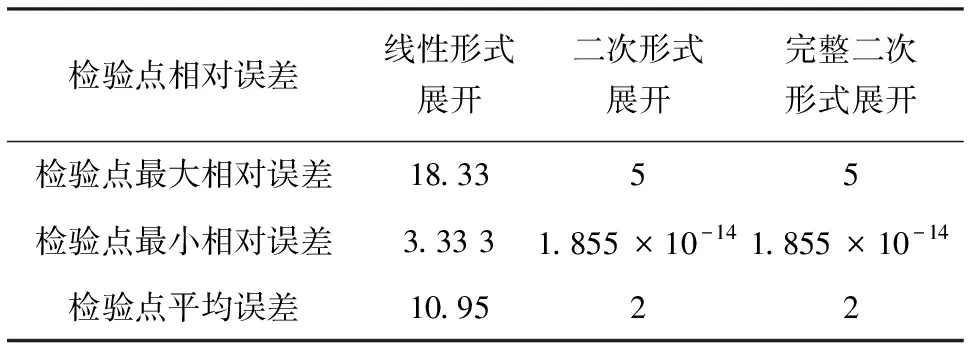
表3 二杆桁架的泰勒展开形式及检验点处的相对误差%

由表3可以看出利用线性形式的泰勒展开求解的精度较差，增加了二阶泰勒展开的响应面求解的精度有所提高，增加了二次交叉项的泰勒展开的响应面验算点处求解的精度变化不大，平均相对误差可以控制在2%左右，验算点处的精度能够满足工程实际的需要，可认为求解结果是准确的，同时与表1对比分析可知基于泰勒展开的响应面方法求解的精度比利用传统多项式基响应面方法求解的精度有了明显的提高，因此可以构建二次形式的基于泰勒展开的响应面方程，实现该结构的隐函数的显示化.

4.2 六杆超静定桁架

利用基于泰勒展开的响应面法求解验算点的结果与通过结构的解析解求得结果的相对误差见表4.

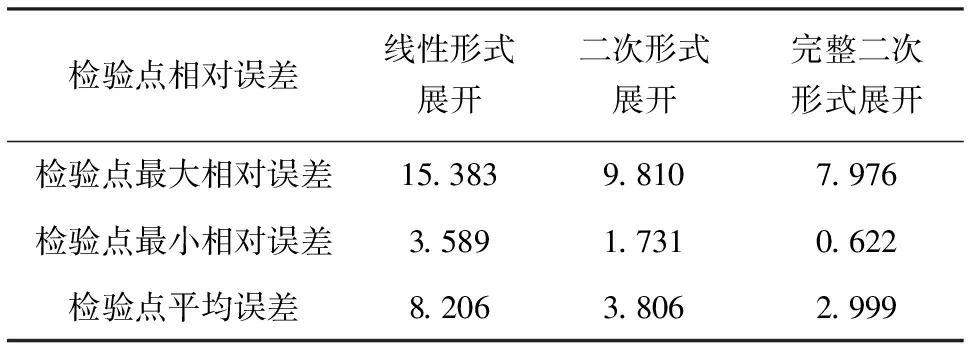
表4 六杆桁架的泰勒展开形式及检验点处的相对误差%

由表4可以看出来，增加了二阶泰勒展开的二次型和完整二次型的响应面方法，求解的精度比线性展开的形式有所提高，基本能够保证工程实际的需要；同时与表2对比分析可知基于泰勒展开的响应面方法求解的精度比利用传统多项式基响应面方法求解的精度有了明显的提高.因此可以构建含交叉项的完整二次形式的基于泰勒展开的响应面方程，实现该结构的隐函数的显示化.

传统的响应面方法本质上是在零点作泰勒展开，而文中提出的方法是在设计变量的中间值做泰勒展开，因此拟合精度会比传统方法高；同时通过数据的变化趋势分析可知越远离展开点相对误差越大，本文的方法是在一个较小的区域内才能获得较好的精度，此时可采用文献[4]中介绍的运动极限的计算方法给出运动极限的粗估，并限制泰勒展开的步长来保证解的有效性和准确性.

5 结论

1)通过桁架算例分析表明传统多项式基响应面在处理桁架问题时拟合精度较差.

2)基于传统多项式基响应面算法存在的问题，提出了基于泰勒展开的响应面方法,并通过区域网格划分和差分公式的推导给出了该算法中各阶偏导数的求解公式.

3)通过桁架结构的算例分析，验证了本文提出的基于泰勒展开的响应面方法，能够有效地提高桁架结构的位移求解精度问题，并通过运动极限的合理设置能够高质量的实现桁架结构优化设计中隐函数的显式化.

[1] 孙焕纯,柴山,王跃方,等.离散变量结构优化设计[M].大连：大连理工大学出版社，2001.

[2] Box G E P,Wilson K B.On the experimental attainment of optimum conditions (with discussion)[J]. Journal of Royal Statistical Society,1951,13(1):1-45.

[3] Myers R H,Montgomery D C. Response surface methodology: process and product optimization using designed experiments, [M].New York:John Wiley&Sons,Inc,1995.

[4] 隋允康,宇慧平.响应面方法的改进及其对工程优化的应用[M].北京：科学出版社，2011.

[5] 隋允康,张立新,杜家政.基于响应面方法的桁架截面敏度分析和优化[J].力学季刊,2006,27(1):96-102.

[6] 李廉锟.结构力学[M].北京：高等教育出版社.2004.

[7] 钱令希.工程结构优化设计[M].北京:水利电力出版社.1983.