两正态分布总体变异系数差的区间估计

张 千, 李新民

(1.山东理工大学 理学院， 山东 淄博 255091; 2.青岛大学 数学科学学院， 山东 青岛 266000)

对区间估计的一般方法是频率方法，此方法只能在一些简单情形下才能对参数和参数函数给出精确的置信区间，在大量较复杂的情形下，只能利用大样本理论，或自助法，鞍点逼近等方法构造近似区间估计．Bayes方法也可用于区间估计，但前提是需要参数的先验分布，并且不同的先验分布给出不同的Bayes区间，而且一般它不是频率意义下的置信区间，即其覆盖率不等于要求的置信水平．本文采用Fiducial推断[1]方法，这类方法不需要先验分布，而是根据数据给出与参数的后验分布有相同作用的Fiducial分布．它由Fisher[2]首先提出并研究．其后有不少统计学者对之进行讨论． David和Stone[3]讨论了在函数模型下求Fiducial分布的一般方法及有关的推断．Barnard[4]基于枢轴模型研究了Fiducial推断．虽然该类方法未能形成理论体系，但在一些频率方法无法解决，而又没有合适的先验分布的具体问题上，用Fiducial方法给出合理可行的答案，仍很有意义． Weerahandi[5]提出了广义枢轴量和广义区间估计的概念，并通过一些实例进行研究，但并未提出如何构造广义枢轴变量．李新民和李国英利用Fiducial推断方法给出了构造方差分量的线性函数的广义区间估计的一种方法．最近Hannig[6]等也讨论了利用Fiducial推断方法构造广义区间估计，并把所得区间估计称为Fiducial广义区间估计．最近李新民等给出了限制参数空间上求参数Fiducial区间的一般方法，并将之应用于一些模型．徐兴忠和李国英在枢轴分布族中给出了构造参数Fiducial分布的一般方法．李新民和李国英[7]利用广义推断法给出了非平衡设计中方差因素和的置信区间，并且说明了通过Fiducial推断方法很容易构造广义枢轴量．Bootstrap[8]方法是由美国斯坦福大学统计学教授Efron首先提出的，该方法通过对样本的经验分布进行随机再抽样、得到Bootstrap子样本，然后再进行统计量的估计。该方法不仅对于很多统计量已被证明满足大样本的相合性，而且对于小样本分析，更具有其不可替代的优越性。

1 参数Bootstrap区间估计

对于多元正态分布总体，Xi=(Xi1,Xi2，…，Xini)(i=1,2)为取自正态分布总体N(μi,σi)的样本，其中，ni(i=1,2)为第i个样本的样本容量．变异系数为

易知

根据参数Bootstrap方法[4]，用样本均值和方差分别代替总体均值和方差，得到

可以推得

其中Z为标准正态分布随机变量．

用参数自助法计算基本步骤如下：

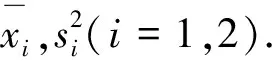
(2)运用Monte-Carlo模拟法，生成一个样本容量ni的Bootstrap样本．

(4)重复上述(2)-(3)步骤n次(一般大于1 000)．

(5)将θB(j)进行升序排列．

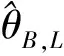
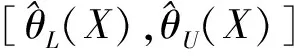
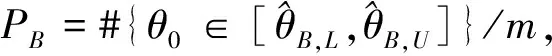
2 Fiducial区间估计

Tsui和Weerahandi[9]及Weerahandi[10]提出了广义推断的概念．设随机变量X的概率分布Pη(·)，η=(θ,δ)为参数空间Ω上的未知参数，θ=θ(η)为所关心的实值参数函数，δ为讨厌参数，记Θ为θ的参数空间，x为X的观测值．

定义1[5]记R=R(X;x,η)为X和x及η=(θ,δ)的函数．如果R满足以下性质：

(1)R的分布与未知参数无关.

(2)r=R(x;x,η)不依赖于讨厌参数δ.

则称R为广义枢轴量．

定义2[6]设存在空间ε上的随机变量E，它的分布已知，并且存在从Ω×ε到χ上的函数h(η,e)，使得当参数为η时，X=h(η,E)．

对一切η∈Ω成立．进一步，若对任意x∈χ和e∈ε，方程x=h(η,e)在Ω上有惟一解，记为ηx(e)．于是

(1)ηx(E)的分布称为η的分布.

(2)θ(ηx(E))的分布称为θ=θ(η)的(边际)分布．

由定义2，从参数θ的Fiducial分布

Fx(θ)=Pr(θ(ηx(E))≤θ)．

易知0≤Fx(θ)≤1，并且Fx(θ)关于θ非减，于是可得到参数的Fiducial区间．

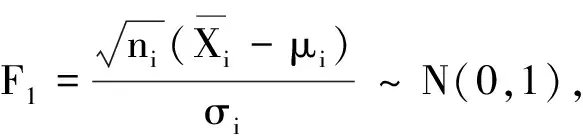
可知COVi的分布与未知参数无关，另一方面，COVi的观测值为

不依赖于讨厌参数，所以COVi为广义枢轴量．

利用广义推断方法,具体的模拟步骤如下：

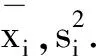
(2)随机产生F1,F2的样本f1,f2．

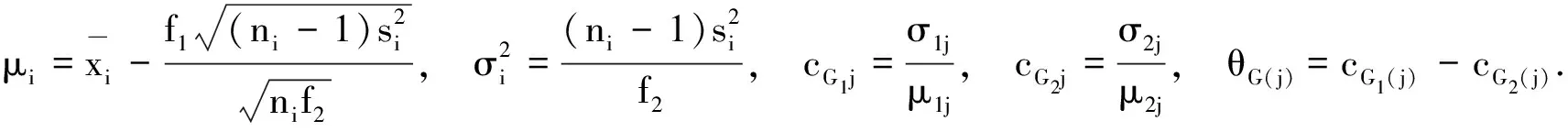
(4)重复上述(2)-(3)步骤n次(一般大于1 000)．

(5)将θG(j)(j=1,2,…，N)进行升序排列．

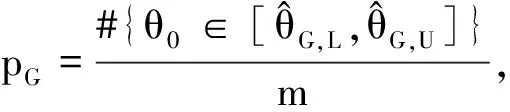
3 实例模拟

3.1 两总体方差相同下的实例模拟

从表1中可以看出，当方差相同时,均值无论怎

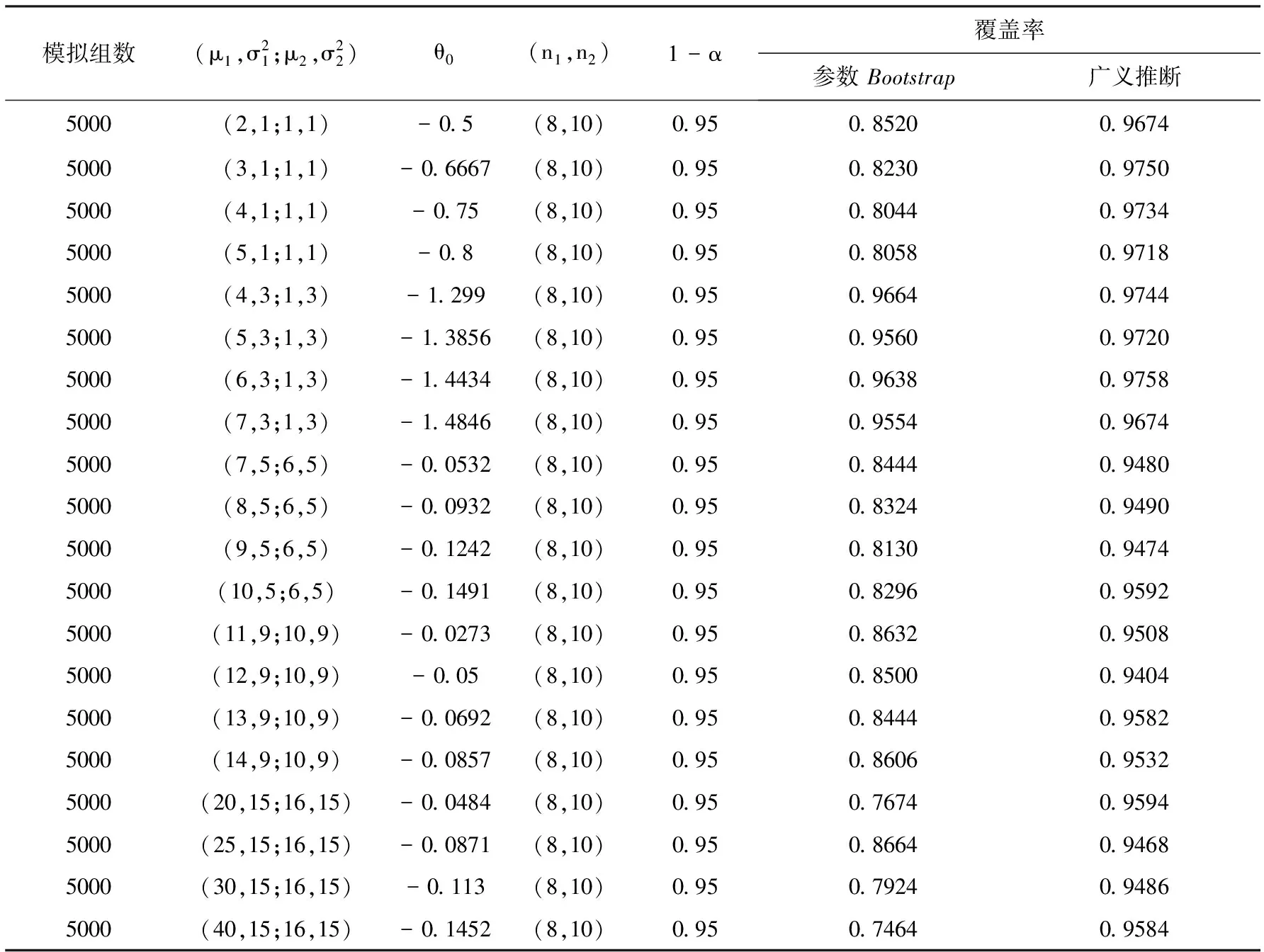
表1 模拟组数相同且方差相同下的精度

么变化，广义推断法的覆盖率比较稳定，并在95%左右,而参数Bootstrap方法的覆盖率一般小于95%且不稳定，所以广义推断法较好．

3.2 两总体方差均值不同下的实例模拟

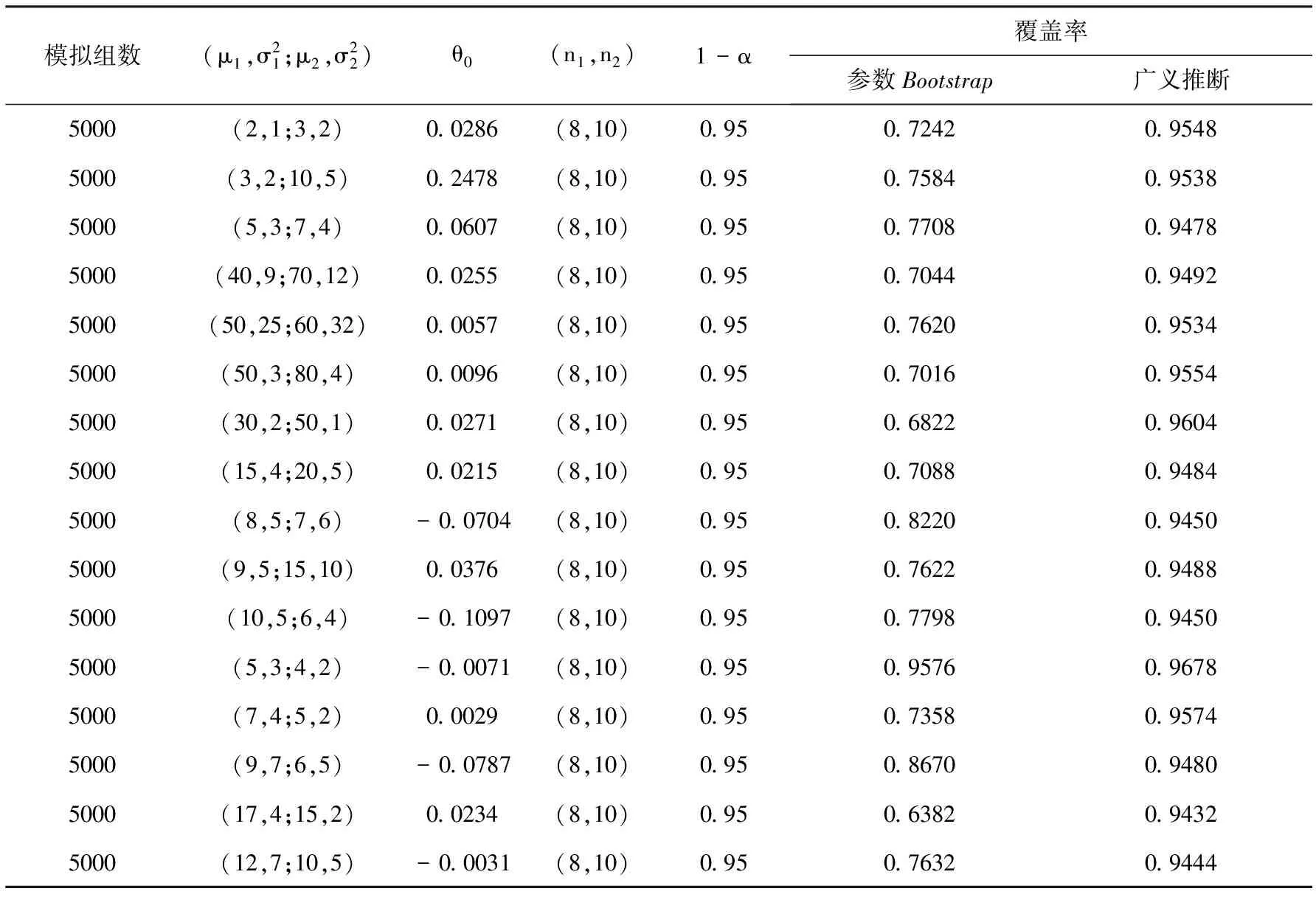
表2 模拟组数相同且均值方差都不同下的精度

从表2中可以看出，当均值和方差任意取值时，广义推断法覆盖率比较稳定，并且覆盖率接近95%，效果较好．

综上知，广义推断法要优于参数Bootstrap方法．

[1] 李新民，徐兴忠，李国英.广义P值的Fiducial推断[J].中国科学A辑:数学，2007, 37(6): 733- 741.

[2] Fisher R A. Inverse probability[J]. Mathematical proceedings of the Cambridge Philosophical Society,1930, 26: 528-535.

[3] Dawid A P, Stone M. The functional model basis of fiducial inference[J].Ann Statist,1982, 10 (4):1054-1067.

[4] Barnard G A. Pivotal models and the fiducial argument[J]. Int Statist Rev, 1995, 63:309-323.

[5] Weerahandi S. Generalized confidence intervals[J]. Journal of the American Statistical Association, 1993, 88:899-905.

[6] Hannig J. On generalized fiducial inference[J]. Statistica Sinica, 2009, 19:491-544.

[7] Li X, Li G. Confidence intervals on sum of variance components with unbalanced designs[J]. Communications in Statistics-Theory and Methods, 2005, 34(4):833-845.

[8] Efron B, Tibshirani R J. An introduction to the bootstrap [M]. New York: Chapman & Hall, 1993, 178-201.

[9] Tsui K, Weerahandi S. Generalized p-values in significance testing of hypotheses in the presence of nuisance parameters[J]. Journal of the American Statistical Association, 1989, 84: 602-607.

[10] Weerahandi S.Generalized confidence intervals[J]. Journal of the American Statistical Association, 1993,88:899-905.