测试性设计的主要目的和具体的实施方法

丁定浩

（中国电子科技集团公司电子科学研究院，北京 100041）

0 引言

测试性设计的主要目的，是要求通过检测性能参数的变化来反映被测对象的工作状态和隔离故障到现场更换模块。这两项任务，要求由机内检测设备 （BITE）来实现。这里所指的状态检测，是反映系统处于正常的工作状态，抑或处于性能退化、功能降级状态，还是已经不能执行规定任务，处于故障状态。这一任务，测试性设计和为测试性服务的BITE设计是一致的。当前对这一功能设计已不存在难点，设计焦点在于一旦发生故障，首先就能快速地隔离到现场故障更换模块，快速地更换故障模块，快速地进行参数校正，实现战备完好对维修保障的要求。

但对故障隔离设计要求，不能混淆对测试性设计与BITE设计要求的差异点。BITE设计的目标是满足要求的故障检测率和隔离率，而测试性设计目标是要求隔离故障到更换模块时间满足相应的平均修复时间中对检测隔离故障时间的限制。

实现快速故障隔离的功能，即减少隔离故障的时间，存在3种渠道的综合权衡设计：1）提高BITE的故障隔离率的设计；2）减少人工 （指专职维修人员使用外部检测仪器和设备）隔离故障时间的设计；3）减少隔离对象数量，也就是兼并现场更换模块以减少隔离对象数量的设计。这对机载设备来说，限于重量、体积的严格约束，不容许BITE过于复杂而增加体积重量，因而大幅度地减少现场更换模块是唯一的出路。由此引发要求现场更换模块数量的增加，可以在现场更换模块中设置内场更换单元，并在邻近现场设置中继站点，承担使用内场更换模块来减轻对备件数量的要求。

实际的BITE设计，必须考虑满足费用、技术、体积和重量的约束，一般难以达到90%以上的水平，也就是说，至少还有10%的概率要依赖人工进行故障隔离。如果人工隔离时间过长，10%的概率平均时间就可能超过平均故障隔离时间的限制；相反，当设法减少人工的故障隔离时间，BITE的故障隔离率为80%也完全有可能满足要求的平均故障隔离时间。因此，文献 [1]最早提出用平均故障隔离时间参数作为测试性设计指标是合理的：

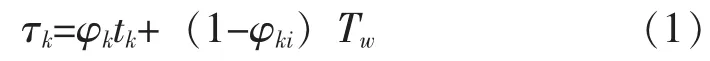
式 （1）中：φk——故障隔离率；

tk——BITE的故障隔离时间，通常小于1 min；

Tw——人工隔离故障时间。

由式 （1）可见，测试性设计的重点是对BITE的故障隔离率设计，以及对BITE不能进行故障隔离的更换模块的人工进行隔离时间的预计和设计。

根据定义，故障隔离率φk与故障检测率是不同的，故障隔离率是在检测率的基础上可以进行故障隔离的比例。由于我们关心的是故障隔离历经的时间，对于实际工程的BITE而言，它的检测隔离对象是各个现场更换模块，对直接连接的各个更换单元来说，故障发生时，能够检测到发生故障的更换模块，也能把故障隔离到这一模块，即故障检测率和隔离率是一致的。但检测与隔离故障历经的时间在特定情况下是不同的。所说的特定情况是指当两个和两个以上更换模块作为一个检测隔离单元的状态。这实际上就是一个隔离模糊组。这时的故障隔离时间就与故障检测时间不同，要增加人工检测时间来鉴别模糊组中的实际发生的故障模块。

根据上述定义，故障隔离率可由公式 （2）表示：

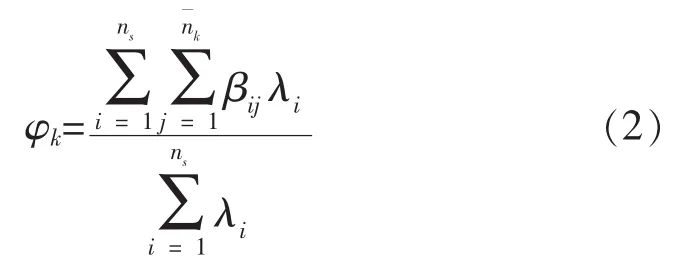
式 （2）中：ns——被测系统中现场更换模块的数量；

αij——第i序号的现场更换模块第j种失效模式的频数比；

nk——BITE可隔离故障的更换模块数。

2 分析设计故障隔离时间的新方法

首先，我们要改进故障隔离时间中有关人工进行故障隔离的表达式，考虑到人工对BITE不能进行故障隔离的各个更换模块的隔离时间的不一致性，系统故障隔离的平均时间模型应改进为：

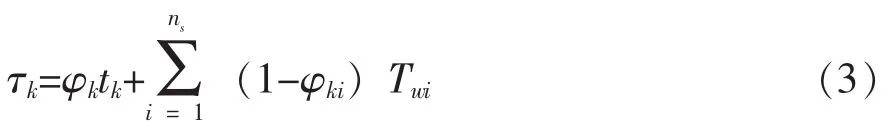
式 （3）中：ns——系统中现场更换模块的数量；

φk——系统故障隔离率；

φki——第i序号更换模块的故障隔离率；

tk——BITE的故障隔离时间；

Twi——第i序号更换模块人工隔离故障时间。

另一方面，难点、繁琐和工作量更大的是确定BITE对检测对象发生故障能够响应的各种失效模式及其频数比αij。为了减轻工作量，我们换一种思路，不求BITE对现场更换模块能够响应的故障隔离率，转而求BITE对现场更换模块发生故障不能响应，即不能隔离故障的失效模式及其频数比βij。于是故障隔离率改变为如公式 （4）所示：

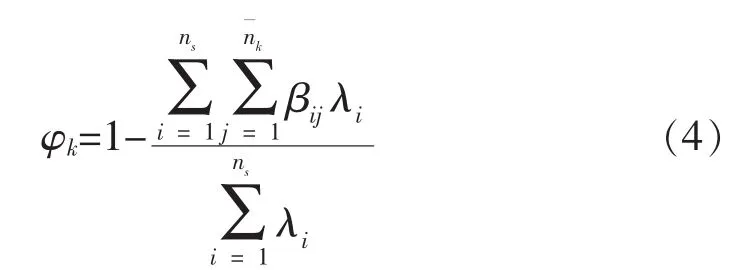
于是，系统故障隔离的平均时间可按公式 （5）计算：

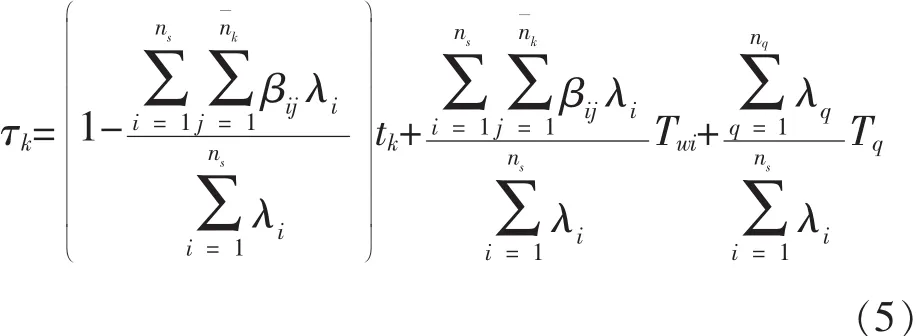
式 （5）中：nq——隔离故障的模糊组数量；

λq——第q序号模糊组内的失效率；

Tq——人工隔离第q序号模糊组的时间；

其他参数同前。

对于不能直接给出BITE对各更换模块的各种失效模式不能响应的频数比βij，可以用BITE对各更换模块不能检测的失效模式频数比作出估计。方法是首先列出BITE不能响应的各种失效模式，并分析产生这些失效模式的相关元器件，计算这些元器件的失效率之和，就是这一模块的失效模式的频数比 βi。

于是故障隔离率和故障隔离平均时间分别为：

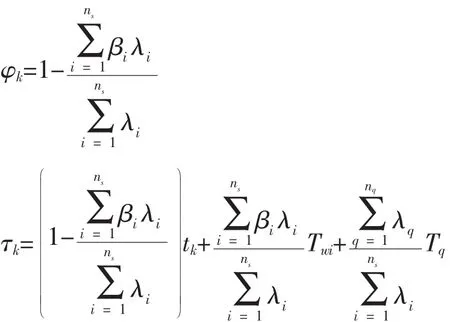
更换模块的故障隔离平均时间，加上它的拆卸重装时间和重装后的参数校正时间，就是这一模块的平均修复时间，战备完好率中更换模块的平均维修延误时间，就取决于再次出动时间和平均维修时间。这为战备完好率设计奠定平均维修延误时间参数。

3 如何降低虚警率

测试性中另一个参数是虚警率，虚警率直接影响装备的战备完好率。虚警率的定义是虚警数与故障总数之比。但如何预计和降低虚警率，迄今未见相应的文献。本文认为：虚警主要来自两个方面。一是在BITE本身发生的故障中导致BIT呈现被测系统出现了故障。这类虚警可以通过对BITE进行FMEA来发现，并作针对BITE这一潜在故障进行改进设计而消除或降低它发生的概率。

虚警的另一来源，是使用门限电平检测参数变化来判别故障的存在。当叠加的噪声的电平超越门限电平，就被误判为失效发生。

消除这类虚警，要掌握检测对象参数变化特性和噪声变化的分布特性，从而正确地设计合理的门限电平。

当测试参数和噪声电平的离散程度一定时，随着设定的门限电平的不同，虚警率和故障检测率或故障隔离率也随之改变，但两者改变的方向是反向的。如图1所示。图中S为检测的参数分布，K是噪声特性，Sil是门限电平。当提高检测电平Sil，从而可以压低虚警率，如图中灰色面积所示，但故障检测率或故障隔离率就压低，如图中黑色面积所示，反之亦然；如果要求既提升故障检测率和故障隔离率，又压低虚警率，则必须设法改变被参数的离散特性，但这不是任何情况下都能实现的。

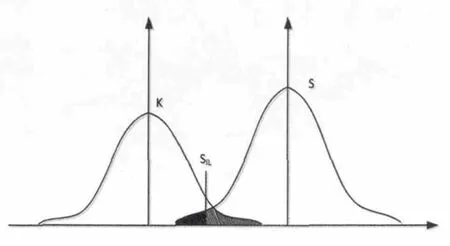
图1 虚警率和故障检测率曲线

4 数字示例

下面举一个数字示例说明确定故障隔离时间的方法和过程。设某型号备件包含40个现场更换模块，首先分析装备中的BITE对各个更换模块的各种失效模式的响应。设45个模块中有22个模块和由3个模块组成的1个模糊组所可能发生的各种失效模式，BITE均能响应，另外对18种更换模块存在若干不同的失效模式不能响应。

设经过分析，已经取得BITE对18种更换模块不能检测、隔离的失效模式频数比βij、要靠人工进行隔离的相应时间Twi。40个更换模块的失效率λi、BITE不能隔离的失效模式频数比βij和相应的人工隔离时间Twi如表1所示，示例中BITE不能隔离的失效模式最多为3项，这是一种假设，实际不受此限。

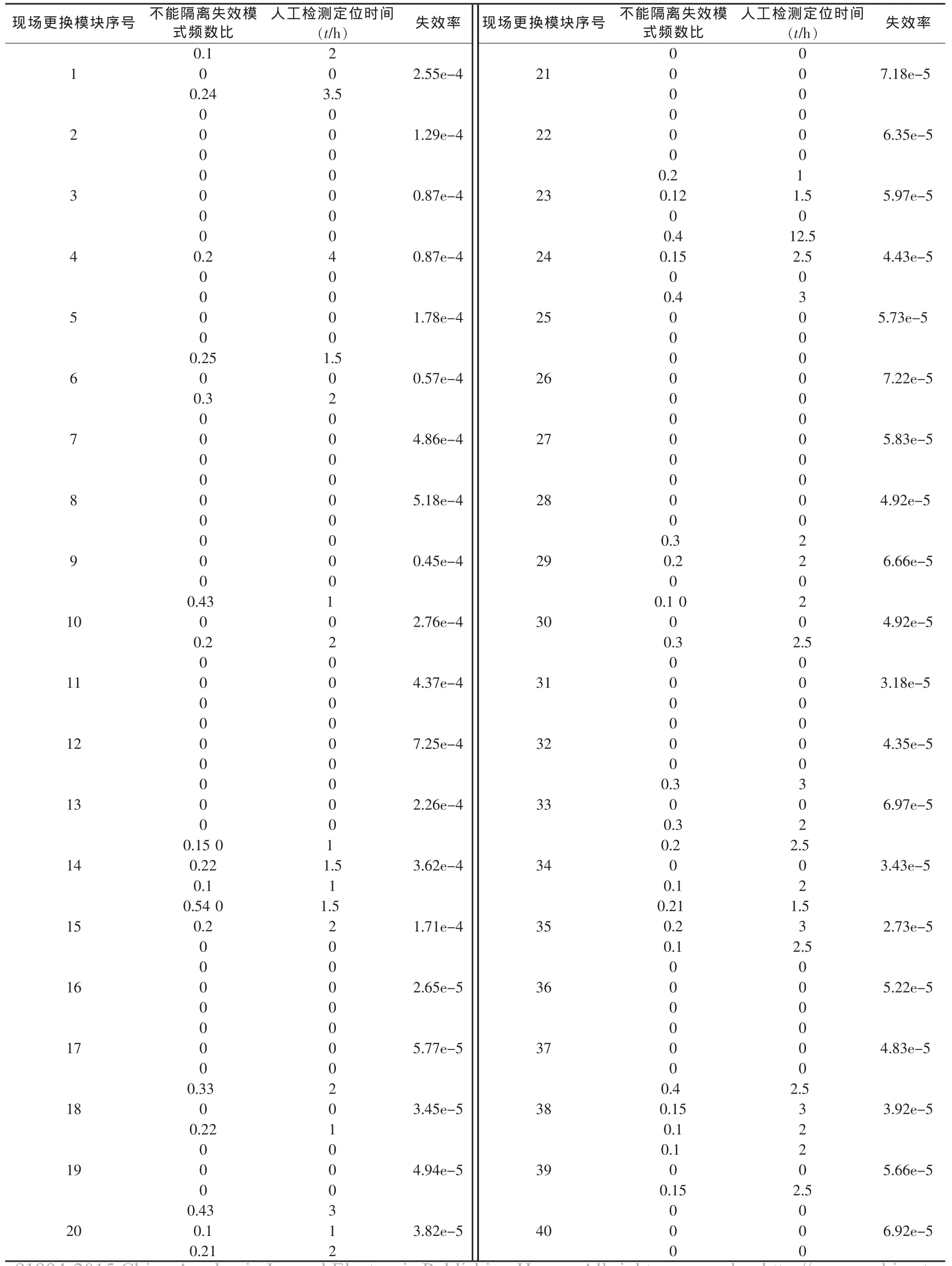
表1 示例数据

此外，还要考虑发生故障BITE能够隔离的1个由3个更换模块组成的模糊组的失效率分别为6.97e-4、5.43e-4、8.86e-4，和人工鉴别3个中那个模块的失效模块的历经时间Tq等于1 h。

上述数据代入系统故障隔离率和隔离时间表达式，使用按上列模型编制的计算软件，不难得到系统故障隔离率为0.84568，故障隔离时间为0.52762 h。

5 结束语

本文提出的计算故障隔离率和故障隔离平均时间的方法，可以大幅度地减少工作时间，又首次提出了一种虚警率的分析方法。同时用示例说明不要专注于故障隔离率的高低，而应该从战备完好率要求出发，关注隔离时间满足要求的设计。示例说明，当得到的小于30 min的故障隔离时间能满足战备完好率需求时，不需追求高的故障隔离率；反之，高的故障隔离率，完全可能存在不满足要求的故障隔离时间。这点应该引起足够的注意。

针对上述分析过程，我们正在研究编制通用计算机软件，在正式推出之前，可以义务服务。

[1] 丁定浩，陆军.装备寿命周期使用保障的理论模型和设计技术 [M].北京电子工业出版社.

[2] 丁定浩.全寿命周期任务可靠度得到持续保持的新系列设计模型 [C]//第四届国防科技工业试验与测试技术发展战略高层论坛文集，2012.