定数截尾试验数据缺失的一些处理方法的探讨
田霆
(华侨大学数学科学学院,福建 泉州 362021)
0 引言
在平时上课给工科学生讲解 《概率论与数理统计》[1](浙江大学版第四章第二节) “基于截尾样本的最大似然估计”时,常常遇到学生提出在处理实际问题时,若遇到数据缺失问题,用常用的统计方法不能很好地解决,在实际应用中遇到此种问题该如何有效地处理。这就需要探讨关于电子产品定数截尾试验中遇到的数据缺失的一些处理方法。
可靠性是产品寿命指标的总称,故产品的寿命指标又被称为产品的可靠性指标,它反映了一个产品在规定时间内和规定条件下,完成规定功能的能力。现在从一个电子元器件、一台电视机到一台设备、一个系统都在研究可靠性指标。随着科学技术的发展,产品的可靠性愈来愈受到人们的重视。
为了弄清被试产品的寿命,求出各项可靠性指标,研究产品的失效机理,以便对提高产品可靠性提出建议,常常需要进行寿命试验。因为只有暴露故障才能了解产品的寿命和失效原因。
寿命试验按样品的失效情况又分为两类:
a)完全寿命试验。这种试验要进行到投试样品全部失效为止。
b)截尾寿命试验。这种试验只是要求进行到投试样品中有部分失效就停止。譬如有50%或70%投试样品失效就中止的试验就是截尾寿命试验。截尾寿命试验又可分为两类:1)试验到事先规定的时间τ就停止的试验,这叫做定时截尾寿命试验(或称为Type-I截尾);2)失效数达到规定的失效数r(<n)就停止的试验,这叫做定数截尾试验(或称为Type-II截尾)。
截尾现象对统计推断产生了一些特殊的问题,其中某些问题现在还未解决,对Type-II截尾,大部分问题的解决都是直接的,其似然函数的性质以及与之相关的一些方法都是容易获得的。Sarhan和Greenberg (1962)[2], 以及 David (1970)[3]的著作中都讨论了次序统计量的一些性质,给出了处理Type-II截尾数据的许多方法。关于其似然函数的一些渐近理论可以在与非截尾样本基本相同的条件下建立起来 (如,Halperin(1952);Johnson(1974))[4]。
1 问题的提出与部分解决方法
在用这些统计方法处理实际问题时,常会遇到数据缺失问题,譬如在产品寿命试验中,由于试验设备、观测手段或有其他方面的困难造成某些试验数据丢失或未观测到的现象等。这样我们得到的是“缺失数据”。若由于部分数据缺失就重做试验一般是不值得的,有的甚至是不可能的。
如何对 “缺失数据”后的现有数据进行统计分析,是一个特殊的、有较大困难的问题。因此,寻找在缺失数据条件下对不完全数据的处理进行科学、有效的可靠性分析方法,现已成为可靠性分析的一个新的十分重要领域。
20世纪70年代对Multiple Type-II截尾样本的统计方法开始有了研究,主要用图估法和回归方法。到90年代以后,研究成果有了较快的发展。Fel和Kong(1994)[5]提出了指数分布参数的区间估计, Fei和 Kong(1995)[6],Balakrishnan,Gupta和panchpakesan(1995)[7]给出了Weibull和极值分布的MLE,AMLE,BLUE和BLIE,Kong和Fel(1996)[8]给出了MLE的渐近正态性的条件,这些条件对Weibull,Gamma,logistic分布等都适用。赵培东 (1999)[9]给出了对数正态分布恒加试验的AMLE的解析表达式。shen和Fel(1999)[10]讨论了两个二参数指数分布位置参数有序约束的估计。
1.1 定数截尾 (缺失数据)指数分布的统计推断
Multiple Type-II截尾 (或称为带有缺失的定数截尾或多重定截尾)样本,在实际中经常遇到。例如:在寿命试验中,对于机理或试验的困难,有些样品的失效时间无法观察到。许多情况是不知道某些样品的确切的失效时间,知道它们在某两个观察值之间。设n个产品进行寿命试验,仅观察到第r1, r2, …, rk个失效产品的失效时间: tr1,n≤tr2,n≤…, trk,n, 其中 1≤r1<r2<…<rk≤n, 在它们之间失效的产品的确切时间未观察到,这种样本被称为Multiple Type-II截尾样本。最近十多年来有关此样本的统计方法有了较多的研究结果,我参见部分国外论文[6,11-12], 国内论文[13-14]只对 Multiple Type-II截尾指数分布的情况稍作了综述,并对下一步需要研究的问题提出了一些看法。
1.1.1 单参数指数分布
单参数指数分布的概率密度函数:

分布函数:
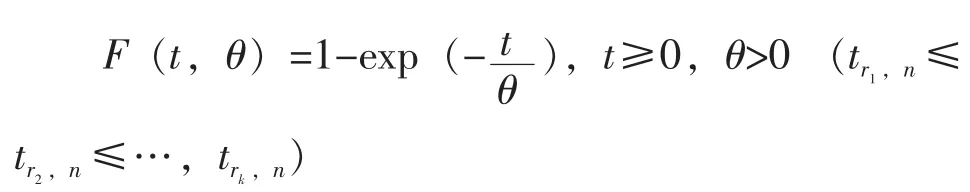
为简单起见, 令 ti=tri,ni=1, …k。
a)最好线性无偏估计 (BLUE)
指数分布次序统计量的期望和协方差:

和



r0=0,的方差为 Var (θ*) =θ2/K。
b)极大似然估计和近似极大似然估计
基于Multiple Type-II样本的似然方程:

上述方程可用数值方法得到θ的极大似然估计。用文献 [10]的方法,利用Taylor展开,得到:


2 结论
在本文中我所考虑的寿命分布都是指数分布。a)在实际的威布尔分布、伽玛分布,以及对数正态分布中也应用广泛。许多类型的产品,如:真空管、滚珠轴承、电器的绝缘材料,都广泛地提倡用威布尔分布。伽玛分布虽不及威布尔分布那样常用,一定程度上是由于伽玛分布的生存函数和危险函数不能以简单的形式表达,因而用起来比威布尔分布困难。然而伽玛分布的确能足以适合广泛的寿命数据,并且一些失效过程模型还可导出伽玛分布。对数正态分布在分析电器绝缘体的失效时间,研究吸烟者中肺癌的出现时间等应用广泛。所以我们可以考虑这些寿命分布下截尾缺失数据的处理问题。b)上述有关理论只是部分学者在处理实际问题时用的一些方法,还有很多学者还有许多好的方法,当然由于很多原因没有列出。
[1] 盛骤,谢式千,潘承毅.概率论与数理统计 [M].(浙江大学第四版).北京:高等教育出版社,2008.
[2] SARHAN A E, GREENBERG B G.Contributions to order statistics[M] .New York: John Wiley&Sons, 1962.
[3] DAVID H A.Order statistics[M].New York: John Wiley&Sons,1970.
[4] HALPERIN M.Maximum likelihood estimation in truncated samples[J] .Ann.Math.Stat., 1952, 23: 226-238.
[5] FEI H,KONG F.Interval estimations for one-and two-parameter exponential distributions under multiple Type-II censoring[J].Commun Statist Theory and Meth,1994, 23:1717-1773.
[6] JOHNSON R A.Some optimality results for one and two sample procedures based on the smallest order statistics.In Reliability and Biometry, F.Proschan and R..J.Serfling[M].Eds.Philadephia, Pennsylvania: SIAM, 1974.
[7] BALAKRISHNAN N, GUPTA S S, PANCHAPAKESAN S.Estimation of the mean and standard deviation of the normal distribution based on multiply Type-II censored samples[M].J Ital statist Soc,1995.
[8] KONG F,FEI H.Limit theorems for the maximum likelihood estimate under general multiply type-II censoring[J].Ann Inst Statist Math, 1996, 48 (4): 731-755.
[9] 赵培东.对数正态分布场合下恒定应力加速寿命试验的多重Type-II截尾样本的AMLE[D].上海:上海师范大学数学科学学院,1999.
[10] SHEN Y,FEI H.Estimating of order-restricted location parameters of two exponential distributions under multiple type-II censoring[J].Appl Math JCU, 1999, 14: 51-56
[11] BALN L J,ENGELHARDT M.Statistical analysis of reliability and life-testing models[M].New York:Theory and Methods, Marcel Dekker, 1991.
[12] FEI H,KONG F,TANG Y.Estimation for two-parameter Weibull distribution and extreme-value distribution under multiply Type-II censoring[J].Commun Statist Theory and Meth, 1995, 24: 2087-210.
[13] 田霆.定时截尾缺失数据下指数分布的统计推断 [D].武汉:华中科技大学,2004.
[14] 田霆,刘次华.定数截尾下双参数指数分布位置参数的统计推断 [J].电子产品可靠性与环境试验,2006,24(3): 36-37.

