更新停止条件对预测维修策略有效性的影响

尤明懿，吕强

（中国电子科技集团公司第三十六研究所，浙江 嘉兴 314033）

0 引言

维修是为保持或恢复产品或系统处于能执行规定功能的状态所采用的所有技术和管理方法[1]。对于已发生或可能发生异常的系统，不但需要采取维修，还需研究如何在维修成本、资源损耗与生产效益之间决策出最优平衡点，由此确定效率最高的维修方式，以达到减少损失、提高可靠性等目的[2]。

随着传感器技术的发展，已可能对各类设备开展连续的状态监测，由此逐渐地发展了基于状态监测的维修策划、预测维修策略等[3]。由于充分利用了设备的在线状态监测信息，在此基础上对设备未来的状态发展做出合理的推断，同时结合维修的目的合理地平衡维修费用与失效风险，预测维修能够有效地提高设备可靠性，降低维修费用，延长设备使用寿命，减小安全隐患等，并逐步地得到学术界的认可与工业界的应用[4]。与基于时间的预防维修策略适用于群体对象的不同，预测维修策略利用设备个体的在线状态监测信息进行维修时间的优化，因而优化的维修时间仅适用于特定的设备。同时，随着状态监测的进行，每个设备的预测维修策略都应随最新的监测信息的到来而进行更新，以跟踪设备状态的最新变化。由此，就产生了预测维修策略中的一个特殊要素：更新停止条件。更新停止条件是指预测维修策略中维修时间的停止随设备状态更新的条件，一旦满足该条件，预防维修时间就即最终确定。

我们在文献 [5]中基于部件级顺序型预测维修模型，提出基于更新步长的更新停止条件：当预测维修模型给出的最近维修时间与当前时刻的距离小于预测维修模型更新步长，即停止更新并立即开展维修。Kaiser和Gebraeel[6]考察了一种基于在线更新衰退模型的部件级预测维修策略，并提出一种基于可靠性的更新停止条件。Curcuru、Galante和Lombardo[7]提出通过在各个决策时刻的规划时段内比较开展预防维修与不开展预防维修的期望费用来判断停止模型更新与否，并最终确定维修时间。Zio和Compare[4]提出在当前时刻达到预测维修模型建议的维修时刻开始维修，或当前状态达到安全状态阈值的概率高于一定的水平时也开展维修工作。

尽管不少学者在预测维修研究中涉及到更新停止条件，但其研究大多注重于预测维修模型的构建与最优维修时间的计算，而未对更新停止条件进行深入的探讨。实际上，正如上文所言，更新停止条件是确定最终维修时刻的重要因素。在设备仍健康运行时过早地停止更新显然是低效的，因其无法在维修时间决策时纳入与设备失效更紧密的衰退过程的状态监测信息。然而，过于激进的更新停止条件也可能因为设备衰退状态的动态变化而导致设备在维修前突然失效。一个好的更新停止条件，也必须与预测维修模型一样，在允许预测维修模型纳入设备更新的状态监测信息与防止设备突然失效之间取得平衡。基于上述考虑，本文致力于研究更新停止条件对预测维修策略有效性的影响。

1 一种部件级预测维修策略

为了建立一个预测维修策略，需定义以下要素[8]：

a）目标，即：维修策略的优化目标；例如：最小化维修总费用，最小化维修费用率，最大化设备可用度等。

b）维修方案，即：维修策略中各维修时间之间的联系；例如：等时间间隔维修方案，基于控制限度的维修方案，顺序型维修方案等。

c）维修效果，即维修后设备状态的恢复情况；例如：修复如新维修，修复如旧维修，修复非新维修 （或称非完全维修）等。

d）退化特性，即：设备状态退化的规律，用于在各个决策时刻估计设备在未来的失效概率；退化模型有：设备统计寿命分布，Gamma过程模型，随机线性衰退信号模型等。

e）维修限制，例如：对设备短时可用度有限制性阈值，多部件系统中无法同时维修多个部件的限制，备件量限制等。

本文建立一种部件级预测维修策略，在此策略中定义更新停止条件。本预测维修策略的要素有：

a）目标：最小化替换周期内的维修费用率。

b）维修方案：顺序型维修方案。

c）维修效果：修复如新。

d）退化特性：随机线性衰退信号模型。

e）维修限制：无。

在该预测维修策略中，若设备在接收预防维修前失效，则立即接受事后替换维修。基于上述要素，该预测维修策略中一个替换周期内某决策时刻t的该替换周期期望维修费用率为：

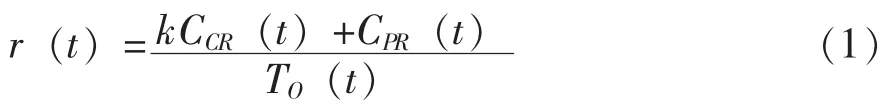
式 （1）中，分子包含两部分：时刻t预计的修复性维修费用期望值CCR（t）、时刻t预计的预防维修费用期望值CCR（t）；分母为该替换周期内设备的期望运行时间。不失一般性，图1给出了该预测维修策略中某决策时刻 （该时刻之前设备正常运行）各时间变量，图中T（t）为时刻t确定的维修 （替换）时刻。

图1 预测维修策略某决策时刻各时间变量

式 （1） 中，CCR（t） 可计算为：

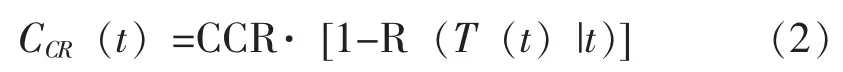
式 （2）中，CCR为进行一次修复性维修的费用，R （T（t）|t）为基于设备至时刻t的衰退信息预测的设备在时刻T（t）的预测条件可靠度。另一方面，CPR（t）可计算为：

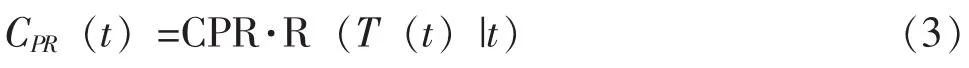
式 （2）中，CPR为进行一次预防维修的费用。 式 （1） 中，TO（t） 可计算为：

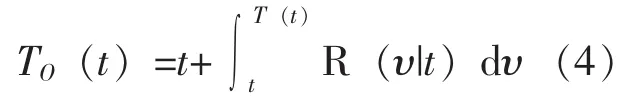
式 （4） 中， R （υ｜t） 为基于设备至时刻t的衰退信息预测的设备在时刻υ的预测条件可靠度，其中υ≥t。基于式 （2）～式 （4）， r（t） 可进一步计算为：

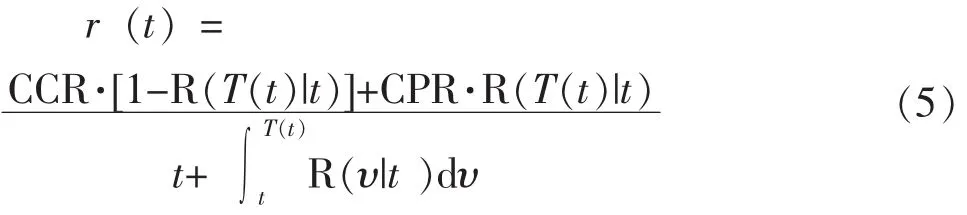
由式 （5）可见，为在时刻t计算使r（t）最小的预防维修时刻T*（t）， 须明确R （υ｜t） 的计算方法。本文基于随机线性衰退模型刻画设备的衰退变量，进而计算R （υ｜t）。随机线性衰退模型为：

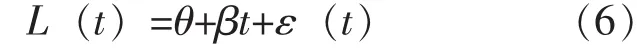
式 （6）中，L（t）为设备在时刻t的状态变量监测值， θ为常数项且 θ～N （μ0，）， 刻画了设备的状态变化率， 且 β～N （μ1，）， ε （t） 为满足布中心朗运动过程的误差项，即ε（t）～N （μ0，σ2t）。在设备运行过程中，将在各个采样时刻获取设备最新的状态变量监测值，Gebraeel等[9]提出了一种基于Bayes法的参数更新方法，论证了采用该更新方法将获得更为精确的设备剩余寿命预测结果。基于模型参数更新结果，可预测设备在时刻υ的条件可靠度，即：

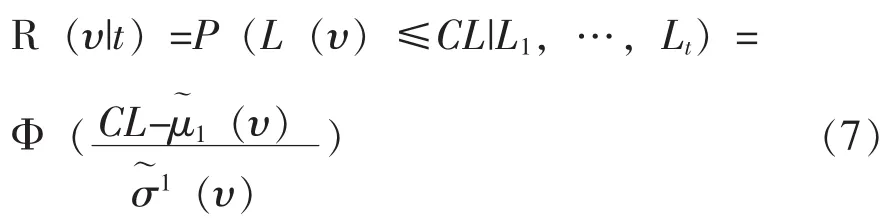
式 （7）中，P（A）指发生事件A的概率，L（υ）为设备在时刻υ的状态预测值，CL为设备状态阈值，一旦设备状态变量超过CL即视为失效，L1，…，Lt指时刻t之前各个监测采样时刻设备的状态变量值，Φ （·）为标准正态分布函数的累计分布函数，分别为：

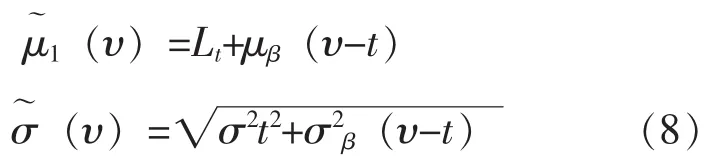
式 （8） 中， μβ、 σβ分别为 μ1、 σ1在当前时刻的更新值。模型参数更新的具体算法可参考文献[9]。 将式 （7） 代入式 （5）， 便可得到：

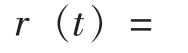
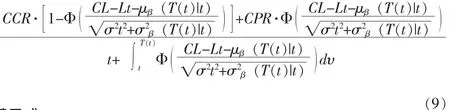
由式 （9）， 便有：

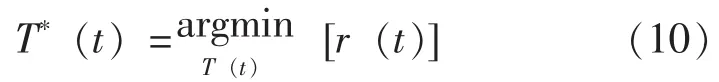
这样，在设备的实际运行过程中，在每个状态监测时刻t，可得到一个最优预防维修时间T*（t）。为有效执行一个预测维修策略，须确定一个更新停止条件，以便在模型参数不断更新的过程中最终确定预防维修时间。本文提出一个基于更新步长的更新停止条件：

式 （11）中，Δt为设备状态监测采样间隔，n为自然数。值得指出的是，式 （11）中的更新停止条件是文献 [5]中更新停止条件的拓展。基于式（11）中的更新停止条件，当某时刻的最优预防维修时刻满足式 （11）中的条件，即停止式 （9）模型的更新，并立即开展预防维修。

2 仿真分析

本部分开展基于随机线性衰退模型的仿真分析，以研究更新停止条件对预测维修策略有效性的影响。

仿真分析的第一步是产生设备衰退信号，并定义设备失效。采用随机线性衰退模型产生设备衰退信号，定义模型参数如表1所示。表1同时定义了设备的失效阈值CL。仿真产生了100个样本，图2演示了3个随机选取的样本的衰退过程，同时给出了失效阈值CL。

表1 随机线性衰退模型仿真参数

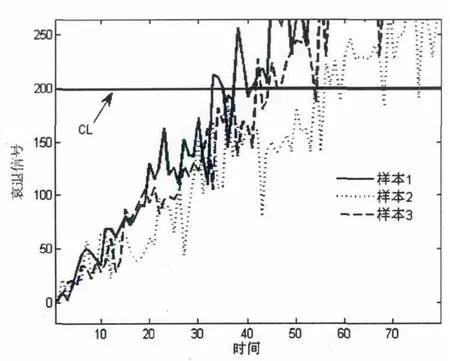
图2 3个随机选取的样本的衰退过程 （σ=4）

仿真分析的第二步是为每个仿真样本在各个采样点建立如式 （9）所示的预测维修模型并计算每个采样点的最优预防维修时间T*（t）。为建立预测维修模型，需定义维修费用参数比CCR/CPR。本文定义CCR/CPR=3和2。这样，基于给定参数的式 （9）便可计算每个样本在其各个状态监测采样点的最优预防维修时刻T*（t）。图3演示了图2中3个样本从开始运行至其失效时刻每个采样点的T*（t）-t。由图3中的结果，某些样本衰退过程中T*（t）-t具有比较明显的趋势，但也存在一些样本，其衰退过程中T*（t）-t随机性较强，这主要是由于样本衰退过程中衰退信号自身的随机性造成的。

图4总结了CCR/CPR=2时，不同σ，不同更新停止条件下 （即式 （11）中不同n的取值）各样本平均维修费用率：

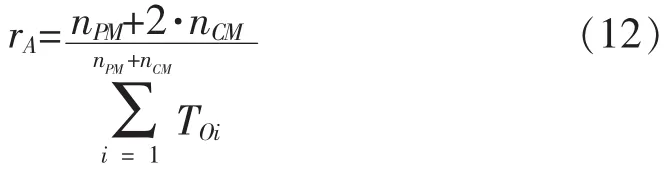
式 （12）中：nPM——全体样本中接收预防维修的样本数；

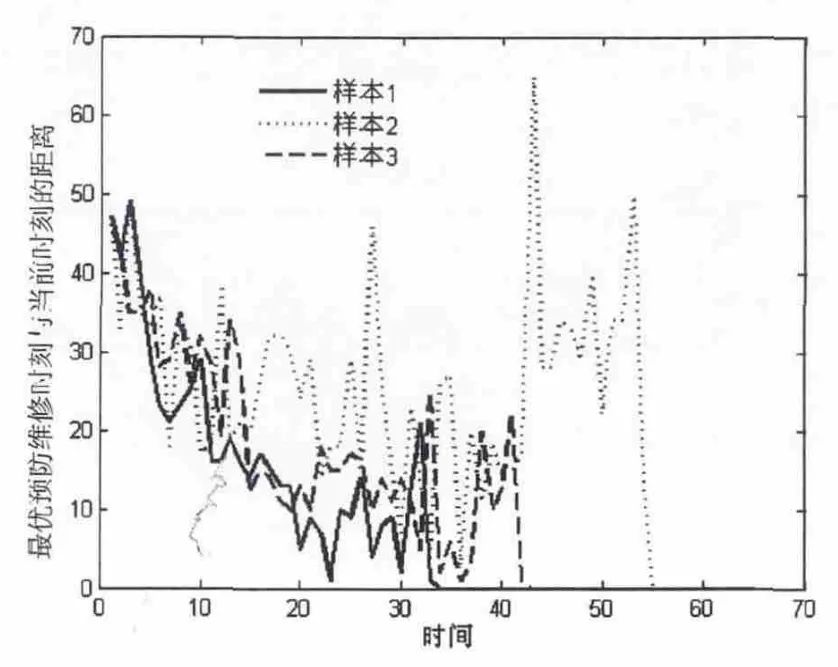
图3 图2中3个样本衰退过程中各个状态监测采样点最优预防维修时刻与当前时刻的距离 （T*（t）-t）

nCM——全体样本中未能接受预防维修而最终失效的样本数；

Toi——样本i的实际运行时间，若样本接收预防维修则Toi等于其接收预防维修的时刻，若样本最终失效则Toi等于其失效时刻。

由图4可见，对于各种衰退过程的噪声水平（σ），更新停止条件对预测维修策略的表现存在显著影响。定性地，当设备衰退过程噪声水平较低时，激进的更新停止条件 （即n较小）能够保证较好的预测维修策略表现；当设备衰退过程噪声水平较高时，则需优化选取更新停止条件以保证预测维修策略表现最优 （本例中σ时，n=11时预测维修策略表现最优）。图5给出了CCR/CPR=3时，不同σ，不同更新停止条件下 （即式 （11）中不同n的取值）各样本平均维修费用率，更新停止条件同样对预测维修策略的表现也存在显著影响。由图4与图5的结果可见，在设备衰退过程噪声水平较高时，特别需对更新停止条件进行优化，才能保证预测维修策略的有效性。

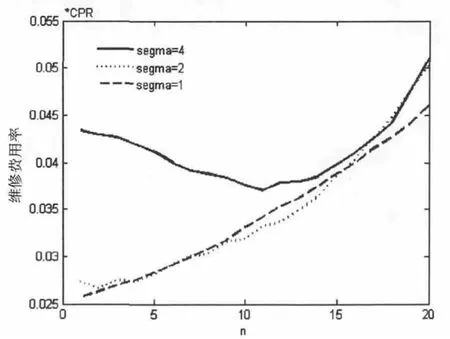
图4 不同更新停止条件对平均维修费用率的影响（CCR/CPR=2）

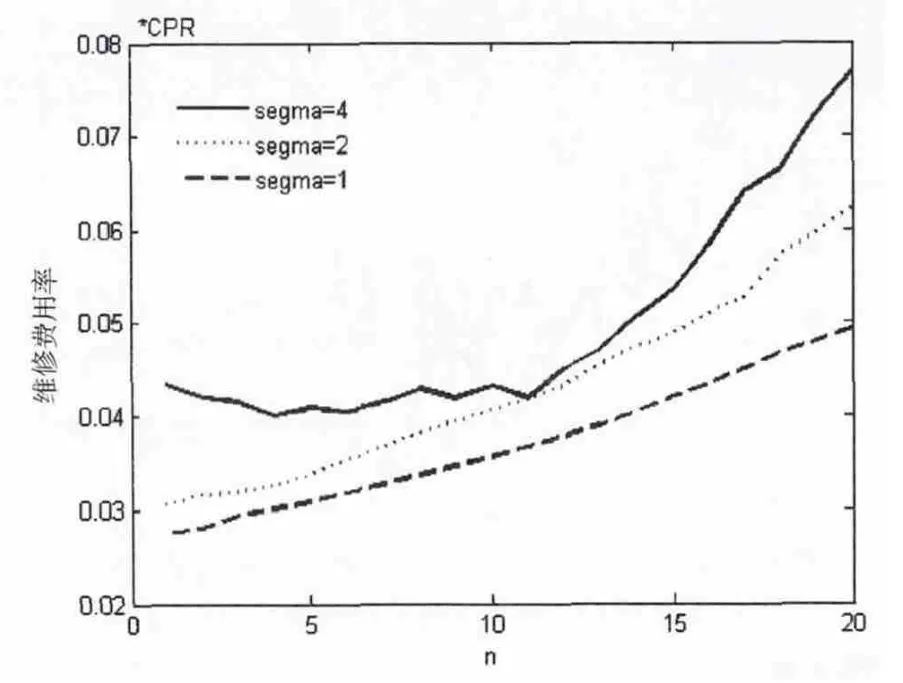
图5 不同的更新停止条件对平均维修费用率的影响（CCR/CPR=3）

3 结束语

建立了一种部件级预测维修策略，在此基础上提出一种拓展的基于更新步长的更新停止条件，通过仿真分析研究了不同事后维修预防维修费用比、不同设备衰退过程噪声水平情况下更新停止条件对预测维修策略有效性的影响。研究表明：不同事后维修预防维修费用比、不同设备衰退过程噪声水平情况下，更新停止条件对预测维修策略有效性均存在显著影响。一个预测维修策略须根据不同的费用参数、衰退过程特性等优化选取更新停止条件，方能最大程度地发挥其效能。本文仅就更新停止条件对预测维修策略有效性的影响程度进行研究，后续的研究尚需考虑实际操作过程中如何基于有限的历史样本优化更新停止条件；此外，对于各类更新停止条件的比较研究也将有助于预测维修策略有效性的提升。

[1] GB/T 3187-1994，可靠性、维修性术语 [S].

[2] 周东华，魏慕恒，司小胜.工业过程异常检测、寿命预测与维修决策的研究进展 [J].自动化学报，2013，39（6）： 711-722.

[3] JARDINE A K S， LIN D M，BANJEVIC D.A review on machinery diagnostics and prognostics implementing condition-based maintenance[J].Mechanical Systems and Signal Processing， 2006， 20 （7）： 1483-1510.

[4] ZIO E，COMPARE M.Evaluating maintenance policies by quantitative modeling and analysis[J].Reliability Engineering and System Safety， 2013 （109）： 53-65.

[5] YOU M Y，LI L，MENG G，et al.Cost-effective updated sequential predictive maintenance policy for continuously monitored degrading systems[J].IEEE Transactions on Automation Science and Engineering， 2010， 7 （2） ：257-265.

[6] KAISER K A，GEBRAEEL N Z.Predictive maintenance management using sensor-based degradation models[J].IEEE Transactions on Systems， Man， and Cybernetics，Part A： Systems and Humans， 2009， 39 （4）： 840-849.

[7] CURCURU G， GALANTE G， LOMBARDO A.A predictive maintenance policy with imperfect monitoring[J].Reliability Engineering and System Safety， 2010 （95）： 989-997.

[8] YOU M Y，MENG G.A modularized framework for predictive maintenance scheduling[J].Proceddings of the Institution of Mechanical Engineers， Part O： Journal of Risk and Reliability， 2012， 226 （4）： 380-391.

[9] GEBRAEEL N Z，LAWLEY M，LI R，et al.Residual life distributions from component degradation signals： a Bayesian approach[J].IIE Transactions， 2005， 37 （6）：543-557.