一种控制增益函数未知的自适应模糊控制
张明君,邵 诚,李世宽
(1.大连理工大学 控制科学与工程学院,辽宁 大连 116024;2.大连大显集团,辽宁 大连 116620)
0 引 言
模糊自适应控制近20年得到了快速发展,在非线性系统控制领域得到了大量应用[1-13].目前,模糊自适应控制主要分为基于模糊建模规则的间接自适应控制和基于模糊控制规则的直接自适应控制[2].间接自适应控制中,模糊系统的语言描述能力被充分用来描述系统,从而使系统中的未知函数可以用模糊模型来建模,文献[3-5]为典型的模糊间接自适应控制.但是对于较高变量维数的系统,或当模糊模型的规则数增加时,上述文献中的控制器计算量将会增长迅速.而直接自适应控制通常采用模糊系统去逼近理想的等价控制器,一般要求系统增益函数已知,或者其界值可估计,但实际应用中界值不易确定,这样可能使控制器的设计过于保守.文献[6-8]中的直接模糊控制方法均需已知控制增益函数;文献[9-11]中均假设控制增益为常数;文献[12-13]中控制方法则是在估计未知控制增益函数界值的基础上设计的,可能使控制器设计具有保守性.
本文在文献[13]基础上,针对含有不确定项的非线性系统,在控制增益函数及其界值均未知的条件下,仅要求控制增益函数为有界函数,设计新颖的等价控制器,应用广义模糊双曲正切模型在线逼近等价控制器,并用一个双曲形式的鲁棒补偿控制项来消除系统中的不确定项和逼近误差,以期实现鲁棒直接自适应模糊控制.
1 预备知识
广义模糊双曲正切模型[14-16]是近年由Zhang等提出的模糊模型,已被证明是一种万能逼近器.
定义1[15]已 知x=(x1(t) …xn(t))T为MISO系统的状态向量,通过平移常数dzj(z=1,…,n,j=1,…,wn)构成广义状态变量=xz-dzj,定义模糊集合P和N的隶属函数分别为
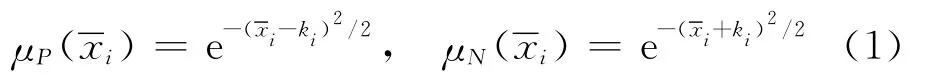
式中:ki为常数.模糊模型的模糊规则(第l条)为
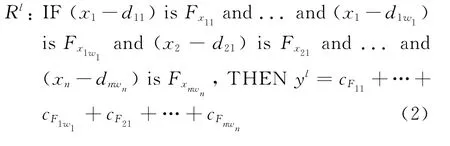
其中Fxzj为广义状态变量=xz-dzj的模糊子集,cFzj是与之对应的常数.系统的输出变量y(t)由各模糊规则推得为
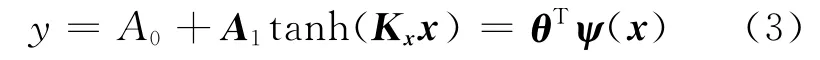
2 控制问题描述
考虑如下形式的SISO 非线性系统:

其中f(x)、g(x)是未知的非线性函数;系统的输入、输出变量为u(k)∈R,y(k)∈R,状态向量为x=(x…x(n-1))T=(x1…xn)T∈Rn,系统的不确定项d∈R有界,包含外部干扰、未建模动态和测量误差项,
假设1[17]非线性系统(4)中的非线性函数f(x)和控制增益函数g(x)未知但有界,即x∈Rn,存在未知边界使得成立.
假设2[17]对于任意x∈D,有g(x)/xn=0,使得

其中D∈Rn表示模糊逼近域,也即(x)只取决于状态向量x.
控制系统(4)的设计目标是,设计一个控制算法,使系统输出y(t)跟踪有界参考信号ym(t).定义e=ym-y为系统的跟踪误差,假设ym具有n-1 阶的各阶导数,定义系统(4)等价表示为

3 鲁棒直接自适应模糊控制算法
由文献[1]知,当f(x)和g(x)均已知,d=0时,对于系统(6)可设计等价控制器

其中K=(kn…k1)T∈Rn使得h(s)=sn+k1sn-1+…+kn的所有的极点均落在左半开平面上,即A-BKT为严格Hurwitz的.
假设Q为满足Q=QT>0的正定对称矩阵,P是满足下列方程的正定解:
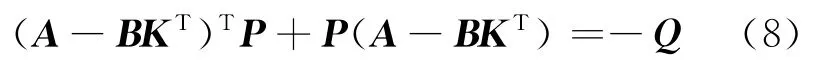
本文对上述控制器修改如下:

因为f(x)和g(x)均未知,且d≠0,用广义模糊双曲正切模型在线逼近上述模糊控制器

注释1 在线逼近等价控制器的模糊模型可以采用模糊基结构的多种模糊模型.本文选用广义模糊双曲正切模型逼近模糊控制器有如下原因:首先,GFHM 已被证明是万能逼近器,可以用来构建模糊控制器;其次,其模糊语言简单易获得,而且模型的数学表达式简单,算法易实现[15].
定义自适应参数θ的约束集为Ωθ={θ∈Rl:θ≤Mθ}.定义最优参数向量和参数误差向量分别为

模糊控制器的最优逼近误差表示为wf=g(x)[u*(x)-uc(x/θ*)].设计系统(6)的总体控制器如下:

其中的鲁棒补偿控制项us在后面给出.注意,此控制器表达式中无控制增益函数g(x)或函数的界值,克服了设计的保守性.
由式(6)、(9)、(12),进一步推得系统的闭环动态方程

定义误差w=(wf-d)/g(x),并假设存在正常数wM,满足w≤wM.把uc(x/θ)=θTψ(x)代入式(13)得

设计鲁棒补偿控制项us和参数自适应律分别为

其中λ∈(0,+∞),r=diag{r1,r2,…,rl},ri∈(0,+∞),l是θ的维数,λ、ri、ε是设计者设定的参数.对比文献[13],本文的自适应律(16)中不再含有未知函数g(x)或函数的界值,克服了设计中的保守性.下面给出鲁棒自适应控制律的有关定理.
定理1 假设形如式(6)的含有不确定项的非线性系统满足假设1、2,同时满足式(8),模糊控制器参数θ未知,则设计的模糊控制器式(12)、(15)及自适应律(16)能够保证系统的所有信号及参数均具有一致有界性;且任意给定ρ>总存在T(ρ)使得t≥T时,其中rmin=min{r1,…,rl}.
证明 选择Lyapunov函数如下:

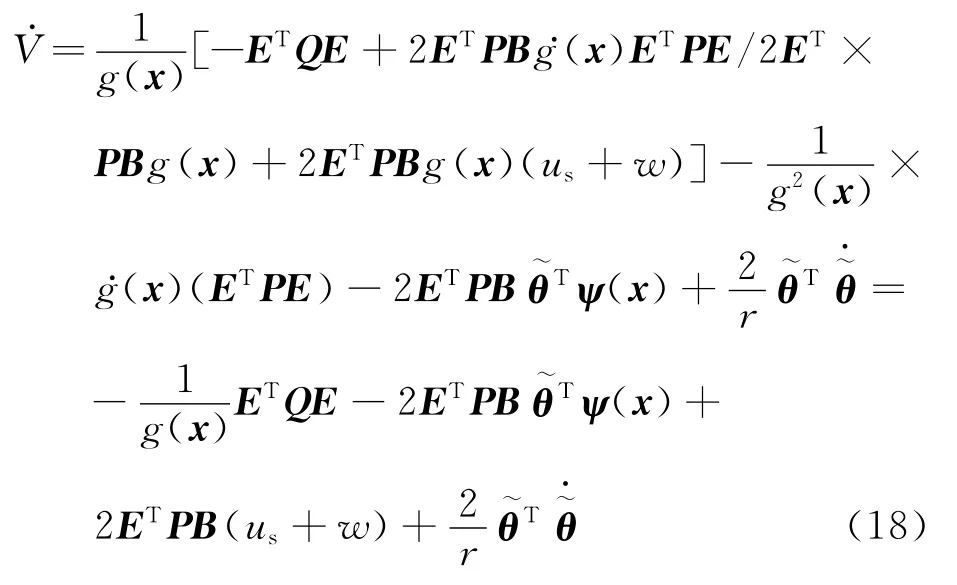
已知对任意的ε>0和η∈R,存在

其中κ为满足κ=exp(-(κ+1))的常数,即κ=0.278 5[5].设η=wMBTPE,把式(15)代入式(18),并应用式(19)得到

把式(16)代入式(20)得



因此,x、θ是一致渐近有界的[18].进一步,对于任意给定的存在T(ρ)使得t≥T时,满足证毕.
注释2 GFHM 是一个全局非线性模型,它由双曲正切函数的集合组成,模糊控制项uc是连续光滑的变量;另一方面,双曲正切函数形式的鲁棒补偿控制项us也是连续光滑的.所以,整个控制输入是连续光滑控制,无切换抖振现象.
注释3 当ε取充分小,rmin、λmin(Q)取充分大时,可以使ρ充分小,即闭环跟踪控制系统的跟踪误差充分小.
注释4 为了确保参数θ∈Ωθ,需要采用投影算法修正参数的自适应律[1].即如果参数在约束集内部或边界,且正向约束集内部移动,则使用基本自适应律;如果参数在约束集边界上,且正向约束集外部移动,则将参数向量的梯度映射到支撑超平面上.应用投影定理修正的自适应律为

其中投影算子

注释5 在定理1 中,函数g(x)的上界只作分析用途,也即在设计控制器(12)时并不需要用到,从而降低了函数界值估计过大导致的控制器设计的保守性.
4 仿真实例
应用上述鲁棒自适应控制算法来控制小车倒立摆跟踪系统.倒立摆的动态方程[5]:

式中:倒立摆的摆角为x1,角加速度为x2.初始条件x(0)= (0.2 0)T,跟踪信号ym(t)=(π/30)sint,其 他参数同文献[5].根据经验取wM=3,应用本文提出的控制算法,取λ=1,(1tanh(0.2x1) tanh(0.4x2))T,外部不确定的干扰d=0.2sin(20πt).

仿真结果如图1所示.图中系统跟踪误差很快收敛趋于零,并且控制输入量光滑连续有界,可见,本文的鲁棒自适应控制算法实现了系统跟踪误差收敛.
5 结 语
本文针对一类含有不确定项的非线性系统,在控制增益函数及其界均未知的条件下,仅要求控制增益函数为有界函数,提出了一种新的鲁棒自适应模糊控制算法,从而降低了函数界值估计过大导致的控制器设计的保守性.本文的控制策略能保证控制系统跟踪误差收敛至充分小,获得较好的跟踪效果,且所有的变量均具有一致有界性.
[1] WANG Li-xin.Stable adaptive fuzzy control of nonlinear systems[J].IEEE Transactions on Fuzzy Systems,1993,1(2):146-155.
[2] PAN Yong-ping,Er M J,HUANG Dao-ping,etal.Adaptive fuzzy control with guaranteed convergence of optimal approximation error [J].IEEE Transactions on Fuzzy Systems,2011,19(5):807-818.
[3] PAN Yong-ping,ZHOU Yu,SUN Tai-ren,etal.Composite adaptive fuzzyH∞tracking control of uncertain nonlinear systems[J].Neurocomputing,2013,99:15-24.
[4] Lin T C,Wang C H,Liu H L.Observer-based indirect adaptive fuzzy-neural tracking control for nonlinear SISO systems using VSS andH∞approaches[J].Fuzzy Sets and Systems,2004,143(2):211-232.
[5] Park J H,Park G T,Seong S J,etal.Outputfeedback control of uncertain nonlinear systems using a self-structuring adaptive fuzzy observer[J].Fuzzy Sets and Systems,2005,151(1):21-42.
[6] HAN Hu-gang,SU Chun-yi,Stepanenko Y.Adaptive control of a class of nonlinear systems with nonlinearly parameterized fuzzy approximators[J].IEEE Transactions on Fuzzy Systems,2001,9(2):315-323.
[7] SU Chun-yi,Oya M,Hong H.Stable adaptive fuzzy control of nonlinear systems preceded by unknown backlash-like hysteresis [J].IEEE Transactions on Fuzzy Systems,2003,11(1):1-8.
[8] Chen C S.Quadratic optimal neural fuzzy control for synchronization of uncertain chaotic systems[J].Expert Systems with Applications,2009,36(9):11827-11835.
[9] Lin C M,Hsu C F.Adaptive fuzzy sliding-mode control for induction servomotor systems[J].IEEE Transactions on Energy Conversion,2004,19(2):362-368.
[10] Wai R J,Chang L J.Stabilizing and tracking control of nonlinear dual-axis inverted-pendulum system using fuzzy neural network [J].IEEE Transactions on Fuzzy Systems,2006,14(1):145-168.
[11] 佟绍成,柴天佑.非线性系统的直接自适应输出反馈监督模糊控制[J].控制与决策,2004,19(3):257-261.TONG Shao-cheng,CHAI Tian-you.Direct adaptive fuzzy output feedback control for uncertain nonlinear systems[J].Control and Decision,2004,19(3):257-261.(in Chinese)
[12] 郑亚琴,刘艳军,佟绍成.具有监督控制功能的非线性系统的直接自适应模糊控制[C]//2009中国控制与决策会议.沈阳:东北大学出版社,2009:918-923.ZHENG Ya-qin,LIU Yan-jun,TONG Shao-cheng.Direct adaptive fuzzy control for nonlinear systems with supervisory control performance[C]//2009 Chinese Control and Decision Conference.Shanyang:Northeastern University Press,2009:918-923.(in Chinese)
[13] 张明君,张化光.一种鲁棒直接自适应模糊控制算法[J].东北大学学报:自然科学版,2006,27(1):5-8.ZHANG Ming-jun,ZHANG Hua-guang.A robust direct adaptive fuzzy control algorithm [J].Journal of Northeastern University:Natural Science,2006,27(1):5-8.(in Chinese)
[14] ZHANG Hua-guang,QUAN Yong-bing.Modelling,identification and control of a class of non-linear system[J].IEEE Transactions on Fuzzy Systems,2001,9(2):349-354.
[15] 全永兵,张化光.广义模糊双曲正切模型及其逼近性研究[J].东北大学学报:自然科学版,2003,24(1):1-3.QUAN Yong-bing,ZHANG Hua-guang.Generalized fuzzy hyperbolic model:a universal approximator[J].Journal of Northeastern University:Natural Science,2003,24(1):1-3.(in Chinese)
[16] ZHANG Hua-guang,WANG Zhi-liang,LIU Derong.Chaotifying fuzzy hyperbolic model using adaptive inverse optimal control approach [J].International Journal of Bifurcation and Chaos,2004,14(10):3505-3517.
[17] Ge S S,Hang C C,Lee T H,etal.Stable Adaptive Neural Network Control[M].Boston:Kluwer,2001.
[18] Corless M.Guaranteed rates of exponential convergence for uncertain systems[J].Journal of Optimization Theory and Applications,1990,64(3):481-494.

