状态概率矩阵及其在GO法中应用
江秀红,段富海,金 霞,魏学东
(1.大连理工大学 机械工程学院,辽宁 大连 116024;2.沈阳航空航天大学 电子信息工程学院,辽宁 沈阳 110136;3.惯性技术航空科技重点实验室,陕西 西安 710065)
0 引 言
故障树分析(fault tree analysis,FTA)[1-2]、故障模式与影响分析(fault modes and effect analysis,FMEA)[3]、Markov链[4]等是复杂系 统可靠性评估中经常使用的方法,但这些传统方法在实际应用中总会遇到不适用于动态系统、计算规模庞大、分析结果不够精确等问题.GO 法(GO methodology)是美国军方为分析武器系统安全性和可靠性而提出并逐渐发展起来的一种可靠性分析与评估方法,最初由美国KAMAN 科学公司提出[5-6].近年来随着其功能和算法的不断发展完善,GO 法在应用中表现出很多独特的优点,已在航空、核电、设备性能分析、电网配电等高可靠领域得到成功应用[7-10].
GO法的分析方法主要有状态组合算法和概率公式算法.状态组合算法需考虑所有信号的状态组合,定量计算比较烦琐,尤其对含共有信号或多重逻辑门的系统,状态组合数可能变得更加庞大而复杂.概率公式算法通过引入信号流状态累积概率,导出GO 操作符的定量计算公式,简化了可靠性的定量计算[6],但对于多状态多输入的系统或操作符(如类型2、6、7等),计算过程仍过于烦琐.为简化计算,目前诸多基于GO 法的可靠性分析与评估都将系统设定为两状态[7-10],这不仅限制了GO 法特长的发挥,也降低了系统分析结果的精度.
本文在状态组合和概率公式两种算法的基础上,提出一种简化的GO 定量计算方法.对部分常用操作符基于概率矩阵的计算公式进行推导,并对文献[11]中共有信号的处理算式进行扩展.通过列写输出与共有信号的多元一次方程组来求解输出状态概率的精确值,打破原算法对共有信号状态个数的限制,以期为多输入多状态共有信号的处理提供一种简易方法.
1 状态概率矩阵的概念
设PS(i)为输入信号的状态 概率,i=0,1,…,N,表示信号流的状态值,0表示提前状态,N表示故障状态,1~(N-1)表示多种成功状态(0~N也可代表有时序问题的多个时间点).按状态值i的大小将PS(i)排列成1×(N+1)维矩阵:
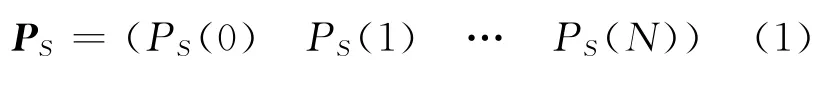
称PS为输入状态概率矩阵,又因只有N个PS(i)线性无关,定义1×N维矩阵P′S=(PS(0)PS(1) …PS(N-1))为输入的独立状态概率矩阵.同样可给出输出和操作符的状态概率矩阵PR、PC及相应P′R和P′C的定义.
假设操作符代表的单元和输入输出信号代表的子系统都是相互独立的,则操作符和输入信号的状态组合联合概率可用它们的概率相乘来得到,引入Φ和Φ′:

可见矩阵Φ中元素对应输入和操作符所有状态组合的联合概率,称为状态联合概率矩阵.同样,定义独立状态的联合概率矩阵

基于这些定义,下面对常用操作符导出输出状态概率的计算公式.
2 概率矩阵定量分析算法
2.1 信号发生器
此操作符没有输入,可直接按输出状态值大小,将对应的状态概率合成输出状态概率矩阵:

若输出不包含状态值i,则相应PR(i)=0.
2.2 两状态单元
用来模拟只有成功和故障两种状态的单元,其独立状态概率矩阵可表示为P′C=(PC(1))n×1,则输入与操作符独立状态的联合概率矩阵
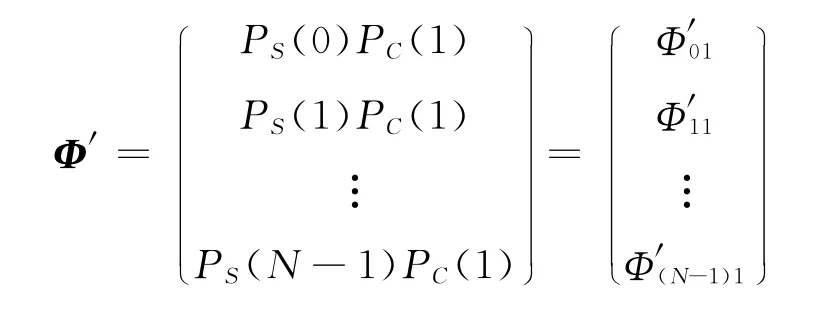
由其运算规则,输出状态概率矩阵可表示为
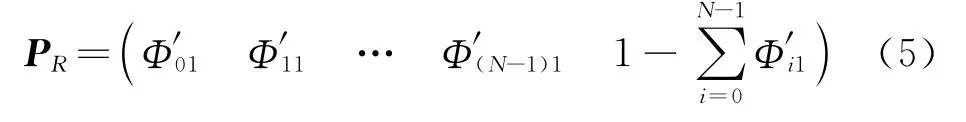
2.3 触发发生器
模拟的单元有3 个状态:提前、成功、故障,PC=(PC(0)PC(1)PC(2)),若输入状态值为0~N,则
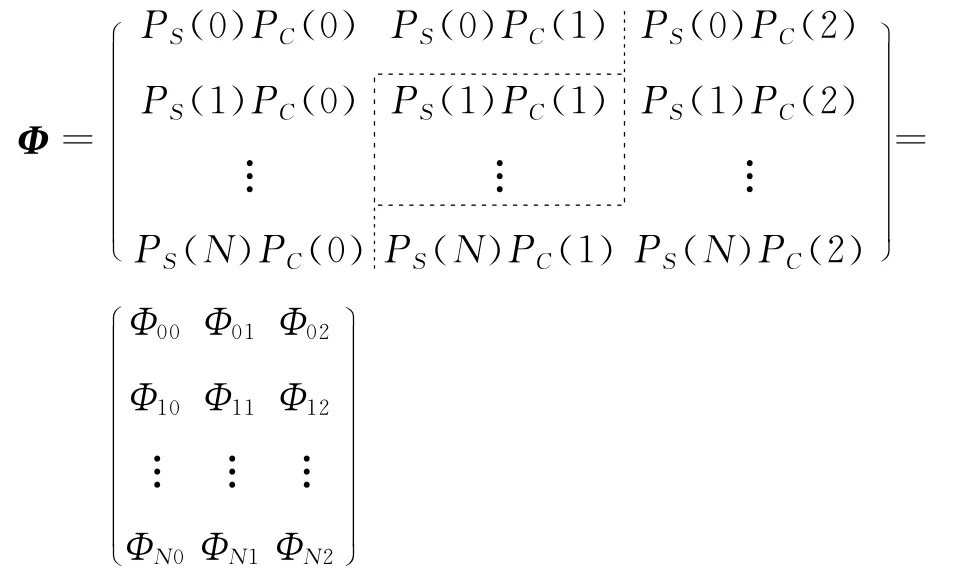
根据其状态组合规则,Φ左上倒“L”区域的元素均为输出提前的联合概率,右下倒“L”区域的元素均为输出故障的联合概率,而中间列剩余元素从上到下依次为输出状态为1~(N-1)的概率,即

2.4 或 门
用来模拟多个信号的或逻辑关系,假设有两个输入PS1、PS2,则令

或门的运算规则是输出所有输入信号中的最小状态值,按这一原则,从Φ左上角开始,第一个倒“L”区域内元素对应的输出状态为0,第二个倒“L”区域对应的输出状态为1,依次类推,最右下角的元素输出状态为N,所以

对于多输入或门,可采用分级方式,按式(7)两两进行计算,前一级的输出再作为下一级或门的输入,也即如有M个输入的或门,则可有M-1次的矩阵相乘.
2.5 与门
与或门一样,假设有两输入PS1、PS2,设两输入状态值均为0~N,则

与门的运算规则是输出所有输入信号中的最大状态值,从Φ右下角开始,第一个倒“L”区域内元素到左上角倒“L”区域内元素,对应的输出状态概率依次为N,…,1,0,所以输出状态概率矩阵为

对于多输入,与门处理过程同或门.
2.6 有动作信号而关断的元件
有主次两个输入信号S1、S2,通过分析其状态运算规则,可将本操作符的运算等价分解为两步.首先,次输入信号S2与操作符之间的关系与触发发生器相同,由式(6)得到二者的输出Rt的状态概率矩阵;其次,求S1与Rt的联合概率矩阵,并求得最终输出R的状态概率矩阵.
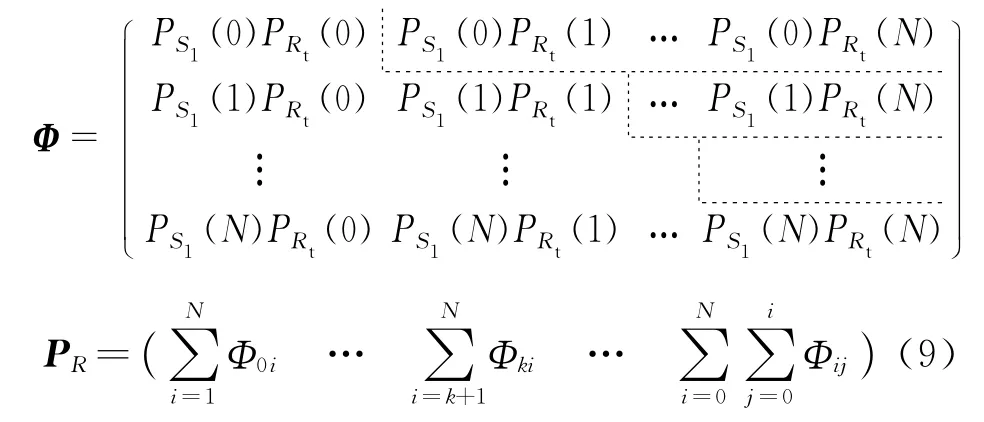
2.7 有动作信号而导通的元件
次输入信号与操作符之间的关系也与触发发生器相同,所以可先由式(6)求得S2与操作符的输出Rt的状态概率矩阵.而S1与Rt的关系相当于与运算,利用式(8)即可求得输出的最终PR.
限于篇幅,只给出上述操作符的运算规则.其余操作符推导过程类似.
3 共有信号的精确处理方法
某些操作符有多个输入信号,若这些输入不是完全独立的,则输出概率需要进行修正.对于简单系统,在输出信号的概率展开式中,直接将共有信号的高次项概率用一次项替代即可.但对于有多个共有信号和多重逻辑门的复杂系统,概率展开式的推导和计算过程将变得很复杂.文献[11]在状态累积概率的基础上提出了一种解决思路,只要对共有信号的状态组合进行多次简单GO 运算,就可得到输出概率的精确值,但此算法只针对具有两状态值的共有信号.本文在概率矩阵的基础上,对文献[11]的算法加以改进.
假设任意一个系统包含2个共有信号S1、S2,则从系统输入开始,经过共有信号修正(一次项代替高次项)后,输出状态概率矩阵一般可表示为

上式可看作多元一次方程组,其中A0、A1、A2、A12为与共有信号无关的未知系数矩阵,P′S1、P′S2、P′R为独立状态的概率矩阵,P′S12为S1与S2的独立状态的联合概率矩阵Φ′组成的向量,即
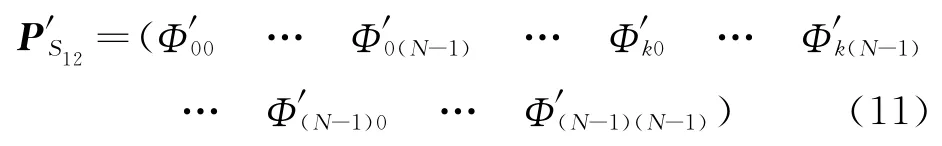
因P′R未知,为了消元,需找出P′S1、P′S2、P′S12与P′R之间的对应关系.又1k=1,0k=0(k=0,1,…,∞),可取PS1(i)=1和PS2(j)=1的状态组合(i,j=0,1,…,N),并在不考虑共有信号修正的情况下,将每一种组合直接进行GO 运算,得到P′S1、P′S2、P′S12与P′R对应的数据对,代入式(10),求得A0、A1、A2、A12.这时方程组中只有P′R未知,将初始正确的P′S1、P′S2、P′S12代入式(10),即可得到修正共有信号后的精确输出P′R.
若存在M个共有信号Si,则输出的独立状态概率矩阵可表示为

其中P′Sk1…kl为P′Sl与P′Sk1…kl-1的联合概率矩阵行向量组成的行矩阵,形如式(11).式(12)是式(10)的推广,M个N状态的共有信号有NM个状态组合,在每一种状态组合下进行直接的GO 运算,然后将特定状态组合下的P′R代入式(12)求得系数A0,…,Ak1…kM,进而得到输出状态概率的精确值.
由以上分析可见,若共有信号状态个数增加,只需增加相应的变量和方程,求解过程依然类似,所以此方法对共有信号的状态个数是没有限制的.
4 算例验证
4.1 概率矩阵算法的一般步骤
图1和表1分别是某设备驱动系统的GO 图和状态数据.

图1 某设备驱动系统GO 图Fig.1 GO diagram of some device driver system

表1 某设备驱动系统状态概率Tab.1 State probability of some device driver system
这是一个四状态系统,应用概率矩阵进行定量计算的步骤如下:
步骤1 确定各输入及操作符的概率矩阵.


步骤2 沿信号流的方向利用概率矩阵公式求各操作符输出概率矩阵.
单元3为有动作信号而导通的元件,由2.7,

由式(8)得PR3=(0 0.855 0 0.145).单元5类型同单元3,同样PR5= (0 0.042 75 0.726 75 0.230 50).单元6为两状态单元,Φ′6=P′TR5P′C6由式(5)得PR6=(0 0.034 2 0.581 4 0.384 4),这也即为最终输出的各状态概率值.
步骤3 共有信号的修正.
若系统不含共有信号,则步骤2的输出即为最终输出,否则需对共有信号进行修正.
4.2 共有信号的修正
图2为某供电系统的GO 图,各单元均无提前状态,状态概率数据为

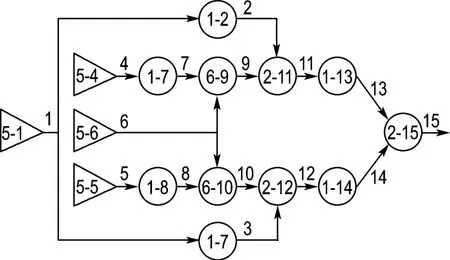
图2 某供电系统GO 图Fig.2 GO diagram of the power supply system
按4.1中步骤,不考虑共有信号求得最终输出PR15=(0.999 998 1 0.000 001 9).但由图2可见,信号流1和6同时输入到多个操作符,属于共有信号,导致信号流13、14非独立,在计算或门15时就需进行修正.
假设信号流1和6相互独立,考虑到共有信号的影响,由式(10)最终输出状态概率可表示为

M=2,N=2,共有信号有22=4个状态组合,各状态组合如表2所示.

表2 共有信号的状态组合Tab.2 State combinations of shared signal
按4.1步骤1和2,重新计算系统的输出成功概率,作为式(13)的常数项,进而求得A0=0,A1=0.999 879 2,A2=0.999 335 6,A12=-0.999 216 4,代入式(13),得到输出的成功概率精确值为P′R15=0.999 879 2×0.995+0.999 335 6×0.999-0.995×0.999≈0.999 990 0,此结果与文献[11]分析的结果一致,证明此方法有效.
5 结 语
GO 法由于其自身的特点和优势,近年来逐步受到重视和发展.本文在状态组合和概率公式两种经典算法的基础上,提出了一种更为直观简便的GO 法定量分析方法——概率矩阵算法.引入了状态概率矩阵和联合状态概率矩阵的概念,通过矩阵相乘和矩阵元素归类实现可靠性的定量分析.此算法通过矩阵相乘列出所有状态组合,不仅便于分析操作符状态和信号流状态之间的组合关系,而且对于多输入多状态的复杂系统,在精简计算复杂度上具有更大的优势.
本文还对共有信号的精确处理提出了新的算式,使应用范围扩展到多状态共有信号,最后通过包含二重或门操作符的供电系统证明了此修正方法的有效性.
[1] Majdara A,Wakabayashi T.Computerized fault tree construction for improved reliability analysis[J].WIT Transactions on Information and Communication Technologies,2010,43(1):149-160.
[2] 贾立德,王金安,杨忠堂,等.基于故障树分析的飞船检漏间泄漏分析与建模[J].宇航学报,2012,33(6):844-848.JIA Li-de,WANG Jin-an,YANG Zhong-tang,etal.Analysis and modeling of leak factors of spaceship leak-testing room based on FTA method[J].Journal of Astronautics,2012,33(6):844-848.(in Chinese)
[3] 周 真,马德仲,于晓洋,等.用于产品可靠性分析的模糊FMECA 方法[J].电机与控制学报,2010,14(10):89-93.ZHOU Zhen,MA De-zhong,YU Xiao-yang,etal.Application of fuzzy FMECA in analysis of product reliability[J].Electric Machines and Control,2010,14(10):89-93.(in Chinese)
[4] 朱正福,李长福,何恩山,等.基于马尔可夫链的动态故障树分析方法[J].兵工学报,2008,29(9):1104-1107.ZHU Zheng-fu,LI Chang-fu,HE En-shan,etal.The dynamic fault tree analysis method based on Markov chain [J].Acta Armamentarii,2008,29(9):1104-1107.(in Chinese)
[5] Chun B B.GO Methodology:Overview Manual[M].Washington D C:Electric Power Research Institute,1983.
[6] 沈祖培,黄祥瑞.GO 法原理及应用——一种系统可靠性分析方法[M].北京:清华大学出版社,2004.SHEN Zu-pei,HUANG Xiang-rui.Principle and Application of GO Methodology:A System Reliability Analysis Methodology [M].Beijing:Tsinghua University Press,2004.(in Chinese)
[7] 金 霞,段富海.基于GO 法的电动静液作动器可靠性分析[J].大连理工大学学报,2013,53(6):846-850.JIN Xia,DUAN Fu-hai.Reliability analysis of electro hydrostatic actuator based on GO methodology[J].Journal of Dalian University of Technology,2013,53(6):846-850.(in Chinese)
[8] 郭昱霄.基于GO 法的复杂配电网可靠性评估及其软件系统研究[D].北京:北京交通大学,2011.GUO Yu-xiao.Reliability and software study of electric distribution system based on GO method[D].Beijing:Beijing Jiaotong University,2011.(in Chinese)
[9] 李 哲,鲁宗相,刘井泉.基于GO 法的核电厂电气主接线系统可靠性分析[J].核动力工程,2010,31(3):69-73.LI Zhe,LU Zong-xiang,LIU Jing-quan.Reliability analysis of nuclear power plant bus systems arrangement based on GO methodology[J].Nuclear Power Engineering,2010,31(3):69-73.(in Chinese)
[10] DU Hui-bin,HU Jia-peng,DU Yu-long.etal.Stated analysis technique of GO methodology for reliability of fire protection systems[J].Advanced Materials Research,2011,183-185:1383-1388.
[11] 沈祖培,郑 涛.复杂系统可靠性的GO 法精确算法[J].清华大学学报:自然科学版,2002,42(5):569-572.SHEN Zu-pei,ZHENG Tao.Exact algorithm for complex system reliability using the GO methodology[J].Journal of Tsinghua University:Science and Technology,2002,42(5):569-572.(in Chinese)

