基于小波神经网络的工业以太网延时预测控制

刘 达，李木国，杜 海

（1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；2.大连海事大学 信息科学技术学院，辽宁 大连 116026）

0 引 言

在控制系统中，为了实现远程控制目的，将控制器和控制对象之间交换的数据用网络来进行传输，就构成了网络控制系统（NCS）.网络的引入，为控制系统带来节省布线、模块化、易诊断、更有效的资源配置及灵活开放等诸多好处，这也是近年来网络化控制兴起的根本原因.然而伴随着网络的引入，延时、丢包、多包传输等问题也给控制系统的分析和设计带来了新的挑战.在应用中，工业以太网可以拥有1 500bit的单包数据容量，基本不受多包传输的影响，并且通过合适的协议设计可有效避免丢包情况的发生，因此网络传输的延时成为控制系统设计需要考虑的首要因素.

网络的延时发生在设备与传输介质进行数据交换的时候，如控制系统的传感器、执行器和控制器与网络交换数据的时候会引入时间的延迟，该延迟时间随控制网络的媒体接入控制协议的不同而呈现为常量、时变或随机值，会对系统的性能和稳定性造成较大的影响，若不加以考虑，可能会降低闭环系统的性能甚至导致系统的不稳定［1］.

随着网络控制研究的深入，网络的延时问题得到众多学者的关注［2］，但是目前尚未有系统的方法来研究网络控制系统，特别是其中的网络延时问题.文献［3］中讨论了一些已有的网络延时控制策略的优缺点，并说明了神经网络适用于预测控制.网络的延时呈现较强的非线性随机特性，而神经网络具有任意逼近非线性函数的特性，因此神经网络在网络延时预测中具有优势［4－7］.小波神经网络可以自适应地调整小波基的形状实现小波变换，并具有良好的函数逼近能力和模式分类能力，而且学习能力强，收敛速度快，因此小波神经网络适于时间序列预测的应用［8－10］.本文采用合适的神经网络结构，设计相应的在线更新算法进行网络系统延时的预测，并应用于对实际工业以太网延时的补偿，同时为说明延时补偿的必要性，对基于网络的永磁同步电机控制系统（PMSM）进行网络延时预测与补偿的对比仿真.

1 基于神经网络的延时预测模型设计

1.1 延时预测模型

为了预测某次采样数据的延时，需要知道该延时前若干个延时的信息，设需要预测的第k次采样的延时为τk，则将已知的τk－p作为神经网络的输入，其中p＝1，…，d，d为神经网络输入节点个数，经过运算，神经网络的输出值即为第k次采样延时的预测值.

选择如图1所示的小波神经网络结构作为网络的延时预测模型，模型由一个输入层、一个隐层和一个输出层组成，wij为输入层节点到隐层节点的连接权重，wjl为隐层节点到输出层的连接权重，其值可通过反向传播算法进行更新，因此该神经网络可以动态地反映控制系统网络的延时状态，输出得到预测延时.

图1 小波神经网络延时预测模型Fig.1 Delay prediction model based on wavelet neural network

隐层神经元的激活函数选择为Morlet母小波基函数，c为正常数：

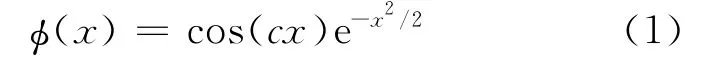
为保证数据处理方便和加快网络的收敛速度，将网络的输入数据归一化至［－1，1］，归一化的映射关系为

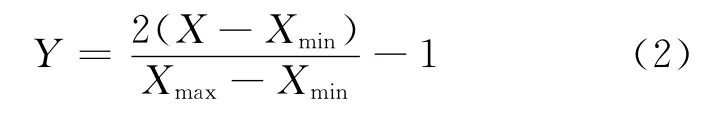
其中Xmax、Xmin分别为输入数据的最大值和最小值，Y为归一化的输出值.经过小波神经网络计算的输出值需经过反归一化处理得到实际的预测值，反归一化的映射关系为式（2）的逆函数：

神经网络的拓扑结构很大程度上影响着网络性能，网络节点的过度冗余极大增加计算的负担且对于收敛精度无贡献，而网络节点太少不能反映出复杂系统或过程的精确非线性关系，因此选择合适的拓扑结构是必要的.Baum－Haussler规则用于近似地选择神经网络中隐层节点个数［11］，原理如下式所示：其中Nh为隐层需要的节点个数，Nt为训练数据集的大小，Np为输入节点个数，Eg为允许的误差大小，No为输出节点个数.

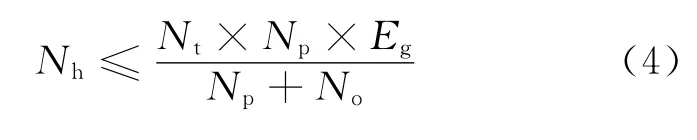
各层的输入输出关系有

输入层：

隐层：

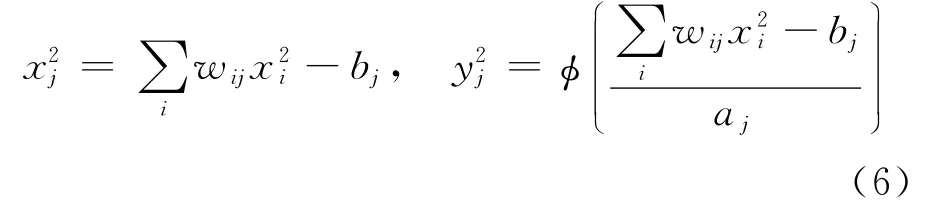
其中aj和bj分别是第j个隐层小波神经元的伸展和平移因子.

输出层：

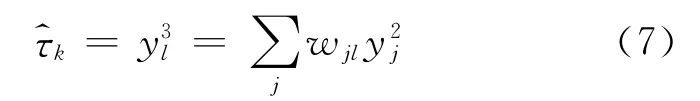
1.2 训练算法

应用小波神经网络预测的最终目的是使实际值与网络输出的预测值的误差最小化，因此可以定义如下的能量函数：

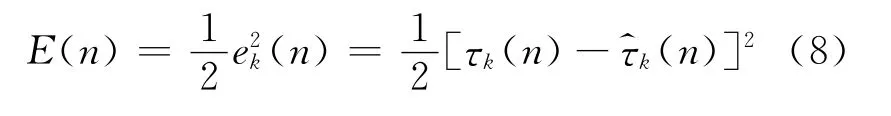
其中n为迭代次数.为求隐层到输出层权重的更新律，将式（8）对wjl求导得

因此wjl可更新为

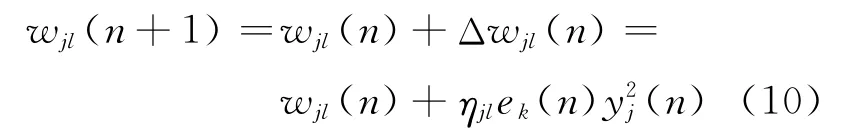
其中ηjl为学习率.

同理将式（8）对bj、aj和wij求导得到其更新律为

其中（·）为式（1）的导数，ηb、ηa、ηij为bj、aj、wij的学习率，若各学习率选取为如下式的定义形式，则可以保证网络的收敛［12］：

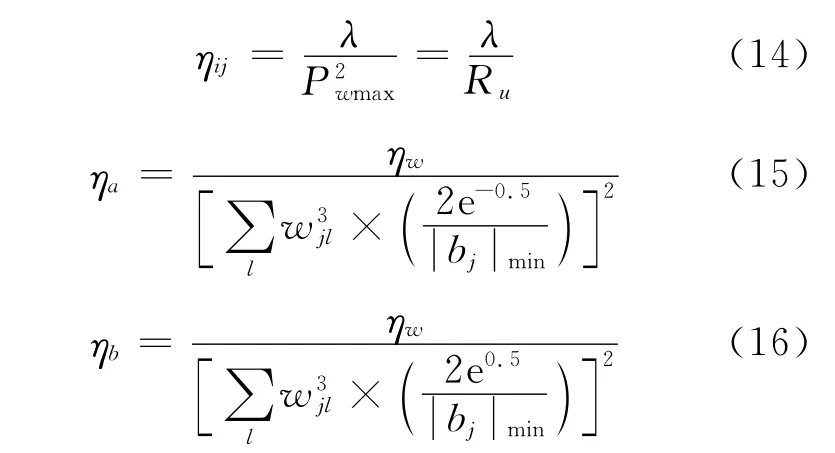
其中λ为大于零的常数，Ru是隐层小波神经元个数，P2wmax、｜bj｜min定义如下：

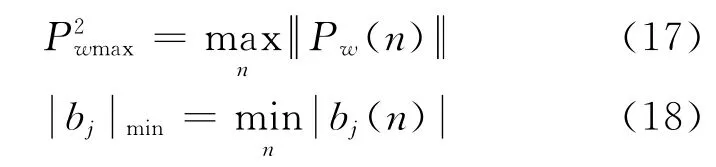
2 预测实验

网络拓扑结构对于预测准确度和收敛时间有很大的影响，在前文介绍的方法基础上，经过多次实验确定网络拓扑结构输入层节点数为5，隐层节点数为10时具有较好的效果.确定网络拓扑结构后，将迭代次数设为50，λ＝1，应用提出的延时预测模型对实际的以太网传输延时数据进行预测.以工业以太网EtherCAT 作为测试对象，采样时间10ms，测得延时样本数据共有300 个延时序列值，将其作为延时预测模型的输入，模型输出即为预测值.为了对比预测效果，将输入的采样延时数据与预测数据绘于一图，得到的预测结果如图2所示.

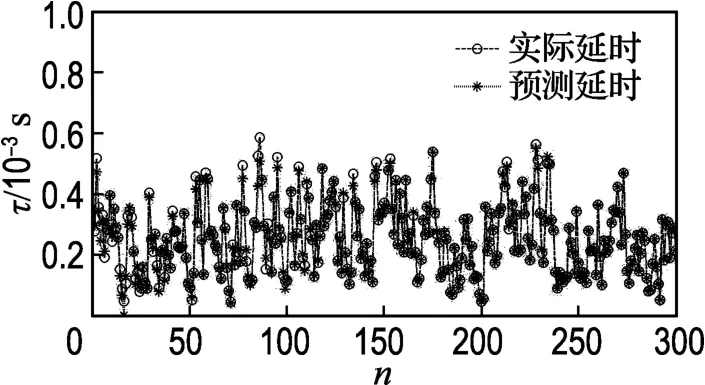
图2 延时序列预测结果Fig.2 Prediction result of delay sequence

由图2可以看出，在初始阶段，延时预测结果误差相对较大，这是由于预测模型输入的样本数据较少，未能获得有效的历史信息，因而无法做出有效的预测，这个问题只在控制系统初始化阶段存在，经过系统初始化后的运行阶段并不受影响.预测结果反映出预测模型的输出可以较好地反映实际网络延时的变化规律，获得了较好的预测效果.虽然预测值与实际值尚存在一定的误差，但是误差值已经远小于实际的延时值，在实际应用中对网络控制系统性能造成的影响基本可以忽略，因此可以通过在控制器端进行补偿以解决网络延时对控制系统的影响.

为进一步验证小波神经网络在预测控制方面具有较好的效果，将延时预测模型中的小波神经网络改为BP 神经网络进行对比.在其他条件不变的情况下，分别用两种神经网络对应的预测模型对采集的5组延时样本数据进行实验，采用定量分析的方法，以实际延时与预测延时数据的方差来表征模型的预测性能，得到的实验结果由表1给出.

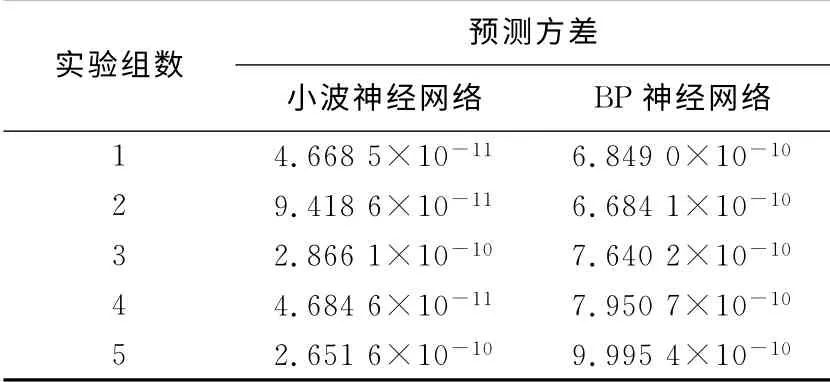
表1 两种神经网络模型的预测性能比较Tab.1 Performance comparison of two neural network prediction models

如表1所示，5 组独立的实验结果表明采用小波神经网络的延时预测模型比采用BP神经网络的延时预测模型的方差更小，有时甚至相差一个数量级，说明小波神经网络延时预测模型具有更好的精度和预测效果，适合于网络延时的预测，并且能够获得较好的性能.

3 应用延时预测补偿的控制系统仿真

为了说明提出的延时预测方法对于网络控制系统设计的有效性，对图3所示的永磁同步电机网络控制系统进行了仿真.图中所示系统为基于网络的速度闭环控制系统，为了分析的方便，将控制器时间延迟和反馈时间延迟合并在一起考虑.出于一般性对比考虑，控制器采用普通的PI控制器，电机系统中采用PMSM 动态模型，控制器输出的信号经矢量控制和空间矢量脉宽调制通过三相逆变桥驱动电机.仿真中考虑到实际应用中可能出现的复杂情况，选取具有较为恶劣网络环境下的延时作为测试对象，对其利用前文提出的预测模型，经过延时预测后通过在控制器端进行延时补偿，调节控制器输出，实现了网络控制系统延时的预测补偿.电机控制系统的参数为线电阻2.9Ω，线电感8.5mH，转矩常数0.675N·m／A，极对数3，转动惯量0.01kg·m2，黏滞摩擦系数0.000 5 N·m／（rad·s－1）.令系统输入速度为100rad／s，仿真时间2s，分别对无网络延时控制系统、有网络延时且具有预测补偿的控制系统及有网络延时而无预测补偿的控制系统进行了仿真，仿真结果如图4所示.

图3 具有预测补偿的PMSM 网络控制系统Fig.3 PMSM networked control system with network delay prediction and compensation

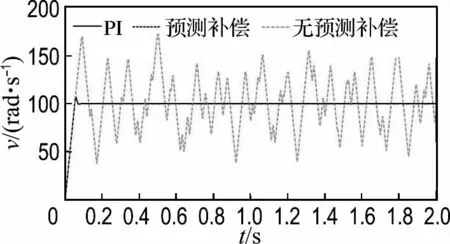
图4 系统仿真结果对比Fig.4 Comparison of the system simulation results

由仿真结果图中可以看出，控制系统的性能在具有较大网络延时的情况下受到了严重影响，若不采用预测补偿的方法，在网络延时的作用下，控制器无法利用正确的反馈数据进行控制，控制量的输出出现较大的误差，造成了系统的不稳定，产生了振荡；而采用预测补偿后，系统延时对系统的影响被大大削弱，电机的动静态性能与无网络延时情况下的控制系统相同，说明通过预测模型的补偿，系统的控制性能及稳定性得到了保证，从而验证了提出的预测补偿方法的准确性和有效性.

4 结 语

工业以太网存在的延时对控制系统的性能和稳定性产生了不利的影响，本文针对这一问题提出了一种基于小波神经网络的延时预测模型，该模型利用神经网络的自学习自适应特性，通过分析记忆已输入的信息，对下次采样时的网络延时进行预测.网络的参数由训练算法更新，能够实时输出各采样时刻的预测值，用于系统对网络延时的预先补偿.利用实测的以太网传输延时数据样本对提出的预测算法进行了实验，结果显示该算法预测性能良好，预测结果准确.为进一步说明预测模型的延时预测效果及对控制系统补偿的效果，将其应用于基于网络的永磁同步电机控制系统并进行了网络延时预测与补偿的对比仿真.系统仿真结果证明了预测模型预测的准确性及补偿的有效性，从而表明通过设计延时预测与补偿策略，控制系统在存在延时的网络环境下依然能够保证较好的控制效果和稳定性，解决了网络延时影响系统控制性能的问题.

［1］ Ray A.Network access protocols for real－time distributed control systems［J］.IEEE Transactions on Industry Applications，1988，24（5）：897－904.

［2］ 聂雪媛，王 恒.网络控制系统补偿器设计及稳定性分析［J］.控制理论与应用，2008，25（2）：217－222.NIE Xue－yuan，WANG Heng.Compensator design and stability analysis for networked control systems［J］.Control Theory ＆Applications，2008，25（2）：217－222.（in Chinese）

［3］ 徐淑萍，苏小会.神经网络预测远程控制系统中信息延时的研究［J］.计算机工程与应用，2012，48（17）：119－122，147.XU Shu－ping，SU Xiao－hui.Research of information delay in neural network forecast remote control system ［J］.Computer Engineering and Applications，2012，48（17）：119－122，147.（in Chinese）

［4］ 于晓明，蒋静坪.基于神经网络延时预测的自适应网络控制系统［J］.浙江大学学报：工学版，2012，46（2）：194－198，231.YU Xiao－ming，JIANG Jing－ping.Adaptive networked control system based on delay prediction using neural network ［J］.Journal of Zhejiang University：Engineering Science，2012，46（2）：194－198，231.（in Chinese）

［5］ 任长清，陈之龙，王晓峰，等.基于神经网络预测远程控制系统中信息延时的研究［J］.计算机工程与应用，2003（14）：167－169.REN Chang－qing，CHEN Zhi－long，WANG Xiaofeng，etal.Research of forecasting information time delays with neural network in telecontrol system ［J］.Computer Engineering and Applications，2003（14）：167－169.（in Chinese）

［6］ 刘 灿，刘 克.网络控制系统中学习－预测环节的改进型BP 算法［J］.计算机工程，2004，30（15）：99－100，189.LIU Can，LIU Ke.An improved BP algorithm in learning－prediction part of networked control system［J］.Computer Engineering，2004，30（15）：99－100，189.（in Chinese）

［7］ 王柱锋，李丽春，黄杭美.延时预测内模网络控制系统［J］.浙江大学学报：工学版，2008，42（11）：1885－1888，1893.WANG Zhu－feng，LI Li－chun，HUANG Hang－mei.Internal model control with delay prediction for networked control systems［J］.Journal of Zhejiang University：Engineering Science，2008，42（11）：1885－1888，1893.（in Chinese）

［8］ Ardalani N，Khoogar A，Roohi H.A comparison of adaline and MLP neural network based predictors in SIR estimation in mobile DS／CDMA systems［J］.International Journal of Electrical，Electronic Science and Engineering，2007，1（9）：1129－1134.

［9］ Becerikli Y，Oysal Y.Modeling and prediction with a class of time delay dynamic neural networks［J］.Applied Soft Computing，2007，7（4）：1164－1169.

［10］ Frank R J，Davey N，Hunt S P.Time series prediction and neural networks ［J］.Journal of Intelligent and Robotic Systems：Theory and Applications，2001，31（1－3）：91－103.

［11］ Baum E B，Haussler D.What size net gives valid generalization？［J］.Neural Computation，1989，1（1）：151－160.

［12］ WAI Rong－jong，CHANG Jia－ming.Intelligent control of induction servo motor drive via wavelet neural network ［J］.Electric Power Systems Research，2002，61（1）：67－76.