基于循环谱特征的楼宇室内频谱感知算法
高治军,王洪玉,王 鑫
(1.大连理工大学 信息与通信工程学院,辽宁 大连 116024;2.沈阳建筑大学 信息与控制工程学院,辽宁 沈阳 110168)
0 引 言
无线通信技术的迅猛发展、新的信息技术的诞生,为人们研究楼宇室内环境中主用户信号的频谱感知问题提供了重要的理论依据和技术方法.在诸多新兴的信息技术中,认知网络(cognitive network)成为人们研究的热点,也为有效解决楼宇室内环境下主用户信号的频谱感知问题提供了关键技术和方法[1].
认知无线电的概念于1999年被提出且其原理被系统阐述,已成为认知网络研究的基础,快速、准确、有效地进行频谱检测是认知无线网络实现正常工作的前提,是认知网络的关键技术之一[2-3],为解决楼宇室内环境中普遍存在的主用户信号频谱感知性能低的问题提供了有效方案.目前,常见的频谱检测算法有能量检测、匹配滤波器检测和循环平稳特征检测算法等[4].能量检测算法具有不需要预先知道授权用户信号的信息,实现灵活,可适合不同中心频率以及不同带宽的检测等优点,但该算法检测门限值的设定比较困难,在信噪比较低的情况下,检测性能不佳,且不能区分信号类型.循环平稳特征检测算法具有较强的抗噪声能力,但其运算量比较大,检测时间长.匹配滤波检测算法具有良好的匹配滤波器能力,但需要掌握主用户信号的先验信息,否则不能达到对主用户的有效检测[5-6].
由于楼宇室内环境中信道的复杂性,目前研究聚焦在多径衰落和噪声不确定性等低信噪比条件下主用户信号的频谱感知问题.文献[7]利用接收信号矩阵的特征值提出了最大最小特征值法(MME)研究主用户信号频谱感知问题,但由于MME算法基于能量检测算法,而能量检测算法不适合低信噪比环境下的频谱感知,其检测结果并不理想;文献[8]和[9]采用机器学习方法来解决认知网络中频谱感知问题,并使用人工神经网络(ANN)算法对主用户信号实现分类检测,但ANN 算法易于陷入局部最优,不能获取最优解,因而影响感知效果;文献[10]将SVM 算法应用于认知无线电环境,提出了采用SVM 算法对高斯噪声环境中的主用户信号进行分类感知的方法,但未对特征参数提取进行更为详细的分析,使得感知精度并不理想.鉴于以上问题,本文针对楼宇室内环境中低信噪比的特点,结合SVM 算法与循环平稳特征检测法对主用户信号的检测性能进行仿真和评估.
1 楼宇室内环境中频谱感知模型
针对楼宇室内环境中主用户信号的频谱感知特点,设室内网络中具有W个主用户和M个次用户,对其中任何一个次用户,系统模型可归纳为一个二元模型:
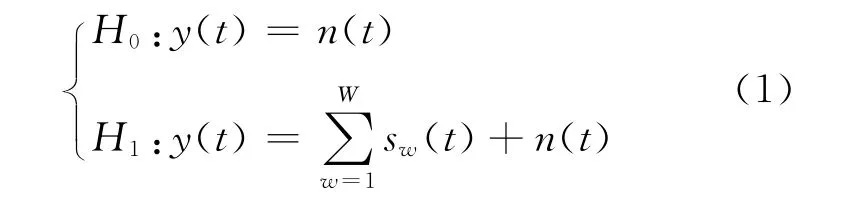
其中H0为无主用户出现情况;H1为主用户出现情况;0≤t≤T,T为接收信号的采样时间;sw(t)为均值为零的楼宇室内循环平稳信号(主用户信号)(w=1,2,…,W);n(t)为均值为零、方差为σ2n的加性高斯白噪声.
基于此二元模型,分别提取H0和H1条件下循环谱特征参数构成的特征向量X0=(E0Mc0Ms0)T和X1=(E1Mc1Ms1)T作为训练样本,利用SVM 对待测样本进行检测,进而达到对主用户的频谱感知.
2 接收信号循环谱特征提取
若零均值循环平稳随机信号y(t)的自相关函数呈现周期性,其循环自相关函数表示为
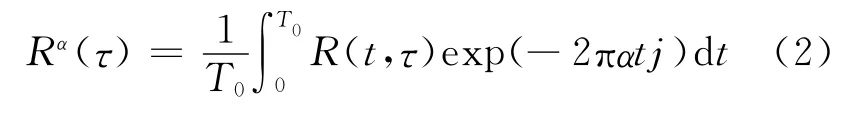
其中α是循环频率,T0为循环周期,R(t,τ)为y(t)的自相关函数.
其循环谱为
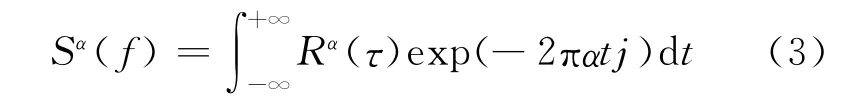
实践中由于使用离散信号,信号长度有限,式(3)可变为

式(4)中,将次用户接收信号y(t)分为N段,每段有T个点,Y(tn,f)为信号y(t)每段的离散傅里叶变换,“*”表示共轭.
信号调制识别需要提取对信噪比和信号调制参数不敏感但对调制类型敏感的参数.因此,可以选择以下3 个参数作为信号调制识别的特征参数.
(1)循环频率处谱函数的平均能量
对于循环平稳信号,其谱函数在循环频率处具有最大信噪比.循环频率处谱函数的平均能量可定义为

其中S(k)为循环谱槇Sα(f)在循环频率α=1/T0处谱函数.如果接收到的信号具有多个循环频率时,取能量最大的循环谱作为S(k).
(2)谱相关系数最大值
谱相关系数作为信号调制识别的重要特征参数,其定义式为
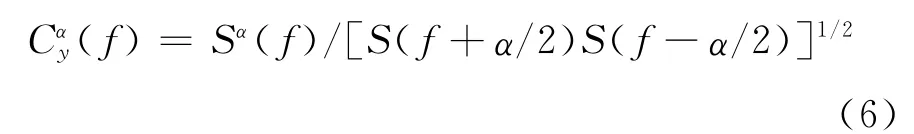
谱相关系数为一个分布在0到1之间的数,取它的最大值MC,即

(3)循环频率α=1/T0处谱函数
取循环频率α=1/T0处谱函数的最大值MS,作为信号调制识别的特征参数,即
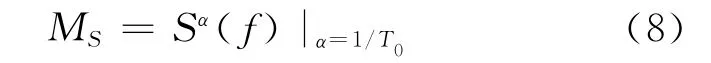
设由以上参数构成的特征向量为X=(EMCMS)T,作为支持向量机的输入.
3 算法设计
3.1 基于SVM 的分类器
支持向量机的核心思想是针对分类中的线性不可分问题,通过非线性变换将输入空间变换到一个高维特征空间,在这个高维特征空间中样本变得线性可分,然后在这个新的特征空间中构造最优线性分类面,从而使线性不可分问题变为线性可分问题[11-12].
对于一个线性不可分问题,假设训练集为{(xi,yi)},i=1,…,l,i为样本数,xi∈Rn,yi∈{+1,-1},n为样本维数,设样本集可以通过下式所示的超平面进行分类:

其中向量w定义了数据不同分类的界限,b为分类门限,(x)=x2/2.
训练向量必须满足下式:

其最优超平面可由求解下式所示的二次规划问题得到:

其中C为惩罚系数.
采用拉格朗日乘数法将式(11)转化为式(12):

其中αi,βi≥0,是拉格朗日乘数因子,对式(12)中w、b、ξi求偏导可得该优化问题的双重表示式:
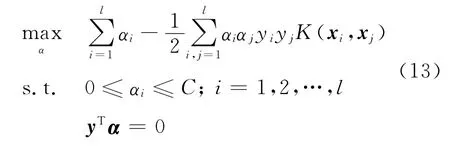
其中K(xi,xj)为核函数,这里采用RBF核函数.
最终获得用于样本分类的决策函数,如下式所示:

3.2 算法的实现
基于接收信号的循环谱特征提取方法,分别提取H0和H1条件下循环谱特征参数构成的特征 向 量X0= (E0MC0MS0)T和X1=(E1MC1MS1)T作为训练样本,利用SVM 对待测样本进行检测.算法实现步骤如下:
步骤1 针对接收信号,采集Q1个主用户存在时的特征向量作为训练的正样本,其中任意一个特征向量为Xi1=(Ei1MiC1MiS1)T,i=1,2,…,Q1;采集Q0个主用户不存在时的特征向量作为训练的负样本,其中任意一个特征向量为Xi0=(Ei0MiC0MiS0)T,i=1,2,…,Q0.
步骤2 将采集到的Q1个正样本和Q0个负样本构成训练集G,并利用训练集G中的样本对SVM 进行训练.
步骤3 重复步骤1,得到的正负样本作为待测样本,利用训练完成的SVM 实现对主用户信号的分类检测.
定义1 设a1表示分类正确的样本数,a0表示分类错误的样本数,则主用户信号检测的正确率可表示为

4 仿真与分析
为了验证本文算法在楼宇室内环境下的性能,对3 种调制信号——AM、BPSK、MSK 使用Matlab7.0进行仿真实验.AM 调制信号使用单频正弦波,其他数字调制信号由随机序列产生,再调制成含有窄带高斯白噪声的窄带信号.仿真的信噪比为-15、-10、-5、0、5dB,在各信号集中分别随机抽取1 000 个样本作为训练样本对SVM 进行训练,再针对每个信噪比对信号集合中每种信号进行1 000次独立测试,循环谱的DFT长度为512.SVM 分类器采用交叉验证方法,选择C=50,σ=0.875.
表1为信噪比为-5dB 和-15dB 情况下,分别使用MME、ANN 和本文算法(C-SVM)对3种调制信号分类所得的正确率.仿真结果表明,随着信噪比逐渐降低,对于各调制信号,MME、ANN 和本文算法的检测正确率均有所下降,在信噪比Rsn=-15dB 时,对于AM 信号,本文算法的检测正确率分别高出ANN 和MME 两种算法10.5%和61.8%,对于BPSK 信号和MSK 信号,本文算法的检测正确率也明显高于其他两种算法.
图1为AM 调制信号使用MME、ANN 和本文算法的检测正确率.仿真结果表明,当信噪比在0dB以上时,3种算法均有很好的检测正确率,随着信噪比的降低,MME检测正确率急剧下降,在Rsn=-15dB时,检测正确率仅为18.3%,ANN为69.6%,而本文算法检测正确率为80.1%,检测性能明显高于其他两种算法.

表1 各算法的频谱感知正确率Tab.1 The accuracy rate of the different algorithms for spectrum sensing %

图1 AM 信号下不同算法检测正确率Fig.1 The accuracy rate of the different algorithms for AM
图2、3分别为BPSK 和MSK 调制信号使用MME、ANN 和本文算法的检测正确率.由仿真结果可知,当信噪比低时,MME 算法的检测正确率最低,ANN 算法次之,随着信噪比增加,虽然检测正确率有所提升,但仍低于本文算法.
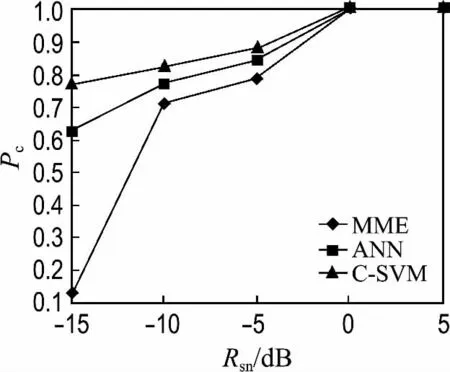
图2 BPSK 信号下不同算法检测正确率Fig.2 The accuracy rate of the different algorithms for BPSK
以上仿真实验结果表明,本文所提算法在楼宇室内低信噪比环境下具有较好的主用户检测性能,而且对AM、BPSK、MSK 不同调制主信号的感知具有稳健性.
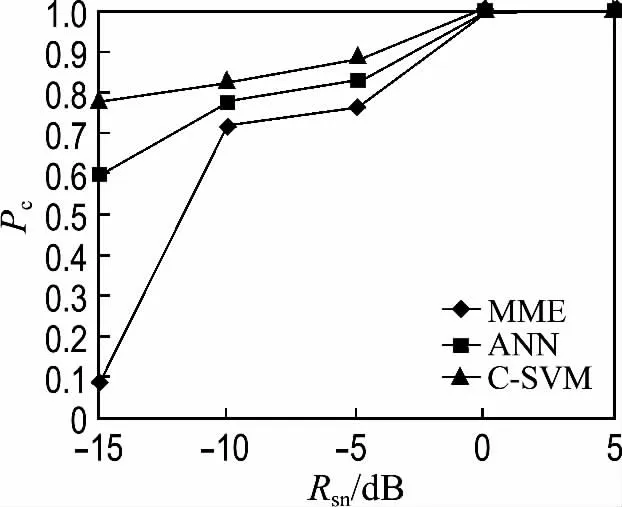
图3 MSK 信号下不同算法检测正确率Fig.3 The accuracy rate of the different algorithms for MSK
5 结 语
本文针对楼宇室内环境中,信道多径衰落和噪声不确定性等低信噪比情况下主用户信号检测性能较低的问题,提出了一种基于SVM 的循环谱主用户信号频谱感知算法.该算法利用对信号循环平稳特征参数进行特征提取,并对SVM 进行训练以实现对待测样本主用户信号的检测.仿真实验结果表明本文所提算法能够较好地克服楼宇室内低信噪比环境对频谱检测性能的影响,有效解决了低信噪比环境下的频谱检测问题,具有较好的主用户信号感知性能.
[1] Devroye N,Vu M,Tarokh V.Cognitive radio networks[J].IEEE Signal Processing Magazine,2008,25(6):12-23.
[2] Yucek T,Arslan H.A survey of spectrum sensing algorithms for cognitive radio applications [J].IEEE Communications Surveys and Tutorials,2009,11(1):116-130.
[3] Wang B,Liu K J R.Advances in cognitive radio networks:A survey[J].IEEE Journal on Selected Topics in Signal Processing,2011,5(1):5-23.
[4] Haykin S,Thomson D J,Reed J H.Spectrum sensing for cognitive radio[J].Proceedings of the IEEE,2009,97(5):849-877.
[5] 王 鑫,汪晋宽,刘志刚,等.基于随机森林的认知网络频谱感知算法[J].仪器仪表学报,2013,34(11):35-41.WANG Xin,WANG Jin-kuan,LIU Zhi-gang,etal.Spectrum sensing algorithm based on random forest in cognitive network[J].Chinese Journal of Scientific Instrument,2013,34(11):35-41.(in Chinese)
[6] SUN Hong-jian,Nallanathan A,WANG Chengxiang,etal.Wideband spectrum sensing for cognitive radio networks:A survey [J].IEEE Wireless Communications,2013,20(2):74-81.
[7] ZENG Yong-hong,LIANG Ying-chang.Eigenvalue-based spectrum sensing algorithms for cognitive radio [J].IEEE Transactions on Communications,2009,57(6):1784-1793.
[8] He A,Bae K K,Newman T,etal.A survey of artificial intelligence for cognitive radios[J].IEEE Transactions on Vehicular Technology,2010,59(4):1578-1592.
[9] DONG Xu,LI Ying,WU Chun,etal.A learner based on neural network for cognitive radio[C]//2010 12th IEEE International Conference on Communication Technology,ICCT′ 2010.Piscataway:Institute of Electrical and Electronics Engineers Inc.,2010:893-896.
[10] HU Hao,SONG Jun-de,WANG Yu-jing.Signal classification based on spectral correlation analysis and SVM in cognitive radio [C] // 22nd International Conference on Advanced Information Networking and Applications.Piscataway:IEEE,2008:883-887.
[11] Cortes C,Vapnik V N.Support-vector networks[J].Machine Learning,1995,20(3):273-297.
[12] Vapnik V N.The Nature of Statistical Learning Theory[M].New York:Springer-Verlag,1995.

