啁啾激光场中氢分子离子电离过程的理论研究

张彩萍，苗向阳

（山西师范大学物理与信息工程学院，临汾041004）

1 引 言

近年，基于原子在强激光场中动力学研究的不断成熟，及激光技术的不断提高，越来越多的学者将目光投向分子在超快强激光中的动力学行为［1-3］.其中氢分子离子作为最简单的研究体系已被广泛应用到分子在强激光场中电离机制的研究中，并取得丰硕的成果.强激光场中的电离理论主要包含电荷共振增强电离（Charge resonance enhanced ionization）［3］，多光子电离（Multiphoton ionization）［4］， 遂 穿 电 离（Tunneling ionization）［4］， 阈 上 电 离（Above threshold ioniza-tion）［5］，跃垒电离（Over barrier ionization）.Bandrauk［6］等人利用激光泵浦技术在非B-O（Born-Oppenheimer）近似下研究处于叠加态的氢分子离子的光电离机制.Ben-Itzhak［7］等人在B-O 近似下研究超短激光脉冲作用下氢分子离子的电荷共振增强电离机制并与Zuo［3］等人的理论解释做了比较.而啁啾场中有关电离过程的研究较少.本文通过使用超短啁啾脉冲（5fs，790nm）进一步探究氢分子离子在强激光场中的电离动力学.

2 理论方法

本文在计算中通过执行LZH-DICP 程序［8］，在非B-O 近似下数值求解了氢分子离子一维含时薛定谔方程：其中体系的哈密顿量可表示为

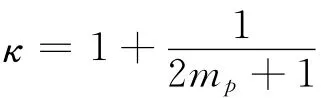
其中高斯外包络函数为

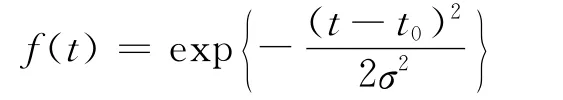
程序中初始波函数通过对角化在分离格点表象（DVR）［8，9］中构建的矩阵中得到，波函数随时间的演化采用二阶劈裂算符［8-11］的方法：

T 为核与电子的动能算符，V 表示体系所有的势能.为了节约时间，将核与电子分开传播得

3 结果和讨论

图1描述了在不同激光强度（4.0×1014W／cm2-1.0×1015W／cm2）下氢分子离子的电离几率随啁啾参数的变化，图中每一点为响应啁啾参数下最大的电离几率C（t）

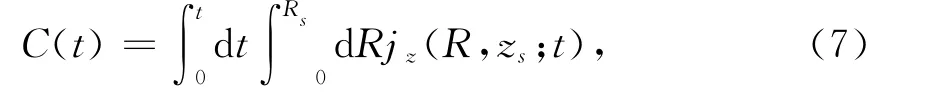
其中jz为流算符［12，13］

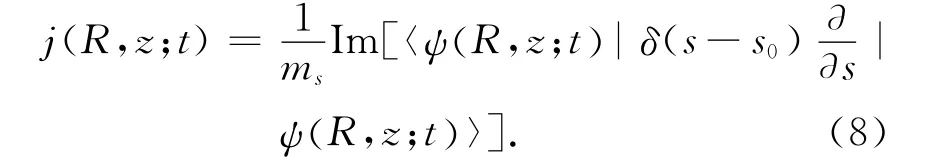
图1 氢分子离子电离几率在不同激光强度下随啁啾参数β的变化.四条虚线代表的激光强度分别为4.0×1014 W／cm2（三角形），6.0×1014 W／cm2（正方形），8.0×1014 W／cm2（钻石形）和1.0×1015 W／cm2（圆形）Fig.1 The ionization probabilities of H+2 with the change of chirp parameterβat different laser intensities.And the four dotted lines represent different laser intensities：4.0×1014 W／cm2（triangles），6.0×1014 W／cm2（squares），8.0×1014 W／cm2（diamonds）and 1.0×1015 W／cm2（circles）

图2 （a）和（b）分别表示β=0和β=6时激光场的变化.（c）和（d）分别表示平均核间距在相应啁啾参数下随时间的变化.其中实线代表激光强度为1.0×1015 W／cm2，点划线代表6.0×1014 W／cm2Fig.2 （a）and（b）show the electronic laser fields atβ=0andβ=6，respectively.（c）and（d）present the corresponding nuclear motion R（t）with the laser intensities of 1.0×1015 W／cm2（solid line）and 6.0×1014 W／cm2（dot-dash line），respectively

本文首先从激光作用后核运动的角度分析啁啾脉冲对氢分子离子电离过程的影响.图2（a）和（b）分别描述β=0和β=6时激光场随时间的变化，随着啁啾参数去值得增大，B 区域的次峰值个数不断增加即随着啁啾参数取值的增大激光频率不断增加.而图1中电离几率从β=0到β=6不断增加主要归因于B 区域激光频率的不断增加.根据公式

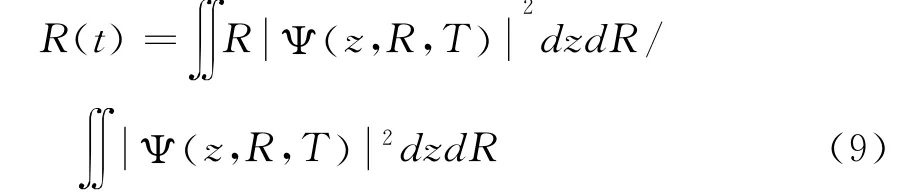
（c）和（d）图分别给出了相应啁啾参数下I=1.0×1015W／cm2（实线）和I=6.0×1014W／cm2（点划线）平均核间距R（t）随时间的变化.从（c）图中可以看出在激光作用前氢分子离子的核间距保持在2.8a.u.，当t=10fs时，氢分子离子开始受到激光的激发，两核运动加快核间距不断增大，而且在激光场的上升区域核间距的增大较快，当t＞18fs即在激光场的下降区域核间距的增加相对较慢.如图所示当激光作用结束后，核间距在较高激光强度下（I=1.0×1015W／cm2）由2.8a.u.增加到7.3a.u.，较低强度下（I=6.0×1014W／cm2）由2.8a.u.增加到5.7a.u..核间距的越大导致核对电子的束缚越小，因而I=1.0×1015W／cm2下氢分子离子的电离几率（0.55）要远大于I=6.0×1014W／cm2的电离几率（0.2）.（d）图为引入啁啾脉冲后β=6时，平均核间距随时间变化，对比（c）与（d）可发现引入啁啾脉冲后，核波包的扩散更显著，核间距迅速增大.两种激光强度下的核间距分别为12.3a.u.（实线）和11.7a.u.（点划线），因而如图1所示在相应的激光参数下电离几率明显增强.从而进一步从核运动的角度解释了啁啾脉冲可增强氢分子离子的电离过程.

图3 不同激光强度不同啁啾参数下电子波包密度随时间的变化.第一列和第二列所对应的啁啾参数分别为β=0和β=6.（a）和（c）所对应的激光强度为1.0×1015 W／cm2，（b）和（d）相应的激光强度为6.0×1014 W／cm2Fig.3 The time evolution of the electronic probability densities at different intensities withβ=0（first column）andβ=6（second column）.The intensities are 1.0×1015 W／cm2 for（a）and（c），and 6.0×1014 W／cm2 for（b）and（d）

为了进一步从电子运动的角度分析氢分子离子的电离过程，根据公式

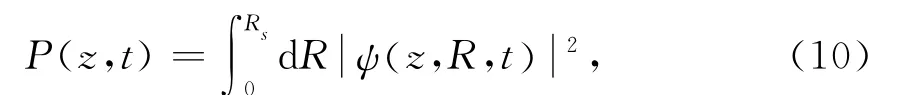
图3描述了不同激光强度下电子波包密度随时间的变化.第一列与第二列所对应的啁啾参数为β=0与β=6，且（a）和（c）相应激光强度为I=1.0×1015W／cm2，（b）和（d）相应的激光强度为I=6.0×1014W／cm2.如图所示，随着激光场周期性的改变，电子在电场力的作用下同样做周期性的运动.在无啁啾激光场中，从（a）图中可以看出在t=18fs，即达到激光的峰值强度1.0×1015W／cm2时，氢分子离子受到强激光的作用，大部分电子被瞬间电离，电子波包密度随之减少.与（a）图比较可发现，当峰值强度为6.0×1014W／cm2时，在18fs到20fs这一时间段内仍由相当数量的电子存在，说明较高的激光强度可有效使电子脱离原子核的束缚，提高电离几率，与图1中β=0时的数值结果相吻合；同理，当氢分子离子处于啁啾激光场中时，随着啁啾参数取值的增大，电子在激光场中的运动也发生明显的改变，如图2（b）中，在B区域内基本不存在电子的分布，即受到啁啾激光的激发后，氢分子离子吸收高频光子达到电离态，电子被瞬间电离.比较（a）（或（c））与（b）（或（d））可以发现啁啾激光场中的电离过程发生的更快些，在适当的啁啾参数下，相应的几率也会有明显的增加.

4 结 论

本文在非B-O 近似下，通过数值求解氢分子离子体系在强激光条件下一维含时薛定谔方程，在超短啁啾激光场中进一步研究氢分子离子的电离过程.研究中有效利用流算符计算得到不同激光强度（4.0×1014W／cm2～1.0×1015W／cm2）下的电离几率，结果表明啁啾脉冲的使用可有效提高氢分子离子的电离几率，且随着激光强度的增大，电离过程对啁啾参数的依赖性增强.通过计算平均核间距及电子波包密度，从核与电子在激光场中运动的角度，进一步说明啁啾激光强度越大，核运动越显著核间距越大，对电子的束缚越小，电子的扩散越明显，从而有效增强氢分子离子的电离过程.通过本文的理论研究，以期人们能够进一步认识强激光场中小分子体系的电离动力学.

致 谢 感谢韩克利研究员提供的LZH-DICP计算程序以及宝贵的指导意见.

［1］ Chelkowski S，Bandrauk A D，Staudte A，et al.Dynamic nuclear interference structures in the coulomb explosion spectra of a hydrogen molecule in intense laser fields：reexamination of molecular enhanced ionization［J］.Phys.Rev.A，2007，76：013405.

［2］ Uhlmann M，Kunert T，Schmidt R.Molecular alignment of fragmenting H+2and H2in strong laser fields［J］.Phys.Rev.A，2005，72：045402.

［3］ Zuo T，Bandrauk A D.Charge-resonance-enhanced ionization of diatomic molecular ions by intense lasers［J］.Phys.Rev.A，1995，52：R2511.

［4］ Posthumus J H.The dynamics of small molecules in intense laser fields［J］.Rep.Prog.Phys.，2004，67：623.

［5］ Paulus G G，Lindner F，Walther H，et al.Measurement of the phase of few-cycle laser pulses ［J］.Phys.Rev.Lett.，2003，91：253004.

［6］ Bandrauk A D，Chelkowski S，Corkum P B，et al.Attosecond photoionization of a coherent superposition of bound and dissociative molecular states：effect of nuclear motion ［J］.J.Phys.B，2009，42：134001.

［7］ Ben-Itzhak I，Wang P Q，Sayler A M，et al.Elusive enhanced ionization structure for H+2in intense ultrashort laser pulses［J］.Phys.Rev.A，2008，78：063419.

［8］ Lu R F，Zhang P Y，Han K L.Attosecond-resolution quantum dynamics calculations for atoms and molecules in strong laser fields［J］.Phys.Rev.E，2008，77：066701.

［9］ Zhang P Y，Lu R F，Zhang A J，et al.Full six-dimensional nonadiabatic quantum dynamics calculation for the energy pooling reaction O2（aΔ1Δ）+O2（aΔ1Δ）→O2（bΔ1∑）+O2（XΔ3∑）［J］.J.Chem.Phys.，2008，128：091103.

［10］ Han J，JI A P，Miao X Y.An isolated 40attosecond pulse generated by using the combination of a two-color laser pulse and a low-frequency field［J］.J.A.Mol.Phys.，2012，29（4）：650（in Chinese）［韩静，吉安平，苗向阳.通过双色激光场和低频电场合成获得孤立40阿秒脉冲［J］.原子与分子物理学报，2012，29（4）：650］

［11］ Liu S S，Miao X Y.Enhancement of high-order harmonic emission by using a coherent superposition in a two-color laser field［J］.J.A.Mol.Phys.，2012，29（5）：881（in Chinese）［刘莎莎，苗向阳.在双色场中使用相干叠加态来提高高次谐波的发射［J］.原子与分子物理学报，2012，29（5）：881］

［12］ Feuerstein B，Thumm U.On the computation of momentum distributions within wavepacket propagation calculations ［J］.J.Phys.B，2003，36：707.

［13］ Feuerstein B，Thumm U.Fragmentation of H+2in strong 800nm laser pulses：initial-vibrational-state dependence［J］.Phys.Rev.A，2003，67：043405.

［14］ Kamta G L，Bandrauk A D.Phase dependence of enhanced ionization in asymmetric molecules［J］.Phys.Rev.Lett.，2005，94：203003.