WmCn（m+n≤7）团簇电子结构与光谱性质

张秀荣，李维军，王杨杨，尹 琳，袁爱华

（1.江苏科技大学数理学院，镇江212003；2.江苏科技大学材料科学与工程学院，镇江212003；3.江苏科技大学生物与化学工程学院，镇江212003）

1 引 言

碳化钨合金具有较高的强度、独特的催化性及优良的断裂韧性等，在生产领域中得到了广泛的应用［1-5］.Karin Mannesson 等［6］利用电子散射衍射和映像分析技术研究了在烧结过程中WC 颗粒的生长行为；Samuel等［7］利用实验对比了WC-与Pt-的光电子图像的角度分布状况，并对WC与Pt的表面反应活性给出了科学的解释；Scharf［8］利用原子探针断层摄影技术和透射电子显微镜，研究了以C-H 为基体的碳化钨晶粒的原子尺寸结构和组成情况，发现在富W 区域内存在W2+、WC2+、C+粒子；Zavodinsky［9］利用密度泛函理论研究了立方晶系和三方晶系碳化钨纳米微粒结构、电子态密度及抗拉强度.在理论上唐国艳等［10］对AlWn团簇的结构与性质进行了详细的研究.近几年，本课题组［11-14］采用密度泛函理论分别研究了Wn（n=1～5）、WnSi02，±（n=1～5）、WmNin（m+n≤7）及WnC0，±（n=1～6）团簇的稳定结构与电子性质，计算结果和相关实验符合的很好.

目前虽然钨碳合金固体材料在工业方面已经得到了广泛的应用，但对于钨碳合金团簇材料的研究还较少，最近本课题组对WmCn（m+n≤7）团簇的几何结构和稳定性进行了系统研究，本文将在前期工作基础上对WmCn（m+n≤7）团簇的自然键轨道（NBO）和振动光谱进行进一步研究，以便为更全面地揭示碳化钨团簇结构和各种物理化学性质随尺寸的变化规律及为实验上制备W-C 纳米材料提供理论参考.

2 计算方法

采用密度泛函理论中的杂化密度泛函B3LYP方法，选用了双ζ价电子基组和相应的Los Alamos相对论有效核势（RECP）即赝势LANL2DZ基组，该基组通过有效核势进行标量相对论效应的修正，适合于过渡金属团簇体系.在计算中对全部优化好的构型都做了频率分析，所得到的稳定构型都是势能面上的局域最小点.所有计算都采用Gassian03程序完成.在进行不同尺寸团簇结构优化和电子结构计算时都未加对称性限制，文献［14］采用的方法和基组与本论文完全相同，所得结果和相关实验数据符合得很好，说明本论文采用的方法和基组对钨碳团簇体系是合适的.

3 结果与讨论

3.1 基态结构

为了找到WmCn（m+n≤7）团簇的基态结构，设计了团簇的多种可能几何构型，并进行了几何参数全优化.构建初始构型时以纯钨稳定构型作为框架，在框架的不同位置以戴帽、置换和填充三种方式构造.优化后得到了WmCn（m+n≤7）团簇的多种稳定结构，图1只列出了团簇的基态构型，同一团簇中较大的球代表W 原子，较小的球代表C 原子.

由图1看出，WCn（n≤6）团簇皆呈线性结构，碳原子之间形成双键，对称性为C∞v，自旋多重度除WC团簇为3外，其余皆为5；当m+n＞4时，基态构型由平面结构逐渐转变为立体结构，基态结构多以不规则的锥形、棱柱形居多，在基态结构中以Wn团簇［15］为结构单元的不多，表明C 原子的掺入破坏了W-W 化学键的形成，而易形成W-C键.

3.2 自然键轨道分析（NBO）

为了进一步分析WmCn（m+n≤7）团簇的自然键轨道成键特性，对WmCn（m+n≤7）团簇基态结构的电荷布局特性和部分成键性质进行了分析.由Pauli不相容原理及能量最低原理可知，原子中电子以1s，2s，2p，3s，3p，4s，3d，4p，5s，4d 等次序排布，从而得出电子组态，W 原子最外电子层排布为5d46s2，C原子为2s22p2.表1详细列出了WmCn（m+n≤7）团簇基态结构各轨道上的NBO 电荷分布，原子序号与图1相对应.

团簇中各原子所处的空间位置不同，当受到不同的势场时致使部分原子失去电荷，另一部分原子得到电荷从而出现电荷转移现象.从表1可知，W原子的6s轨道上的NBO 电荷分布在0.08～0.99之间，5d 轨道电荷分布在4.43～4.99 之间（除WC6和W2C4外），6p轨道上的NBO 电荷分布相对较少在0.02～0.52之间，部分W 原子的6d轨道的NBO 电荷有少量的分布.从上述数据可以看出，W 原 子 的6s 轨 道 失 去 电 子，而5d 轨 道（除WC6和W2C4外）和6p轨道得到电子，与WnC0，±（n≤6）［14］团簇自然轨道电荷转移现象相同.对于C原子来说，2s轨道上的NBO 电荷分布在0.45～1.82之间，NBO 电荷主要集中在2p轨道（除WC6团簇和W2C4团簇外），2p轨道上的NBO 电荷分布在2.70～3.06之间，3s和3p轨道分布的NBO 电荷相对较少.上述数据表明C 原子2s轨道失去电荷，2p、3s、3p 轨道得到电荷.从轨道电荷分布来看，与W 原子相邻的C原子上的2p轨道得到电荷数目大于其2s轨道失去的电荷数目，而W 原子6s轨道失去电子数目大于其5d 轨道得到的电荷数目，说明W 原子部分电荷转移到C原子.从轨道电荷分布进一步分析发现W 原子6s轨道上的电荷转移到了C 原子2p轨道，因此在W 原子与C 原子相互作用的过程中，电荷以从W 原子转移到C原子，在结构中易形成较强W-C键.

图1 WmCn（m+n≤7）团簇的基态结构Fig.1 Ground state structures ofWmCn（m+n≤7）clusters

表1 WmCn（m+n≤7）团簇自然电子组态和电荷Table 1 The natural electron configuration and atomic charge ofWmCn（m+n≤7）

?

从表1进一步发现，WmCn（m+n≤7）团簇中NBO 电荷分布状况与该团簇的对称性相关，对称性较高的团簇中，在对称位置的原子，其NBO 电荷分布状况也相同，如在W2C2团簇（对称性为D2h）结构中，1、2位置上的W 原子上的NBO 电荷分布相同，为6s（0.58）5d（4.72）6p（1.23）；3、4位置上的C 原子上的NBO 电荷分布相同，为2s（1.57）2p（2.93）3p（0.01.同时表1也列出了WmCn（m+n≤7）团簇基态结构中各个原子上的净电荷分布情况，由表1数据可得出：W 原子的净电荷分布在-0.02e～0.71e，C原子的净电荷分布在-0.77e～0.21e，C 原子的净电荷分布比W 原子的净电荷分布范围要大一些，说明C 原子比W 原子的电荷调节能力强，易与其它原子形成化学键.在W 原子和C原子相互作用形的过程中，原子间发生了电荷转移，在相互作用中，W 原子呈正电性，大多数C原子呈负电性，这部分C 原子从W 原子得到电子，在形成团簇的过程中起主导作用，这一点在WmCn（m+n≤7）团簇的平均结合能和Wiberg键级中得到了很好的验证.

3.3 振动光谱分析

图2画出了团簇基态结构的红外光谱（IR）和拉曼光谱（Raman）图，其中红外光谱图中横坐标的单位为（cm-1），纵坐标表示强度，单位为（km·mol-1）；拉曼光谱图中横坐标的单位为（cm-1），纵坐标表示拉曼散射活性，单位为（A4·amu-1），通过GaussView 软件来判断光谱峰值所对应频率的振动方式.

红外振动光谱是分子能级之间的跃迁引起的，多原子分子的振动形式可分解为若干个简单的基本振动，又称简正振动.根据分子光谱整体旋律，高度对称的分子，其振动不引起偶极矩的变化，故没有红外吸收峰，此振动称为非红外活性振动；有些分子在振动过程中有瞬间偶极矩的改变，在红外光谱中出现相对应的吸收峰，这种振动称为红外活性的振动，根据量子理论，红外吸收峰的强度与分子振动时偶极矩变化的平方成正比，偶极矩变化越大，其红外吸峰就越强；拉曼光谱图是一种吸收-发射的双光子过程，它的选律取决于分子运动方向上极化率的改变情况.

从图2可以看出，对于WCn（n≤6）团簇，WC2团簇红外光谱有一个最强振动峰位于1679.47 cm-1处，此峰在所有振动频率最大处，红外光谱强度为313.29km·mol-1，振动模式为C 原子的伸缩振动；拉曼光谱中有两个较强振动峰，最强振动峰位于584.29cm-1处，拉曼活性为55.18 A4·amu-1，振动模式为C 原子与W 原子之间的伸缩振动.WC3团簇红外光谱有一个最强振动峰位于1908.32cm-1处，红外光谱强度为526.08km·mol-1，此峰在所有振动频率最大处，振动模式为2C原子在1C原子和3C 原子之间的伸缩振动；拉曼光谱中最强振动峰也位于频率最大1908.32 cm-1处，拉曼活性为237.41A4·amu-1，振动模式为2C原子在1C 原子和2C 原子之间的伸缩振动.WC4团簇红外光谱有一个强振动峰位于振动频率最大2003.91cm-1处，红外光谱强度为1053.11 km·mol-1，振动模式为C 原子之间的伸缩振动；拉曼光谱中有一个最强振动峰位于1719.19cm-1处，拉曼活性为321.26A4·amu-1，振动模式也为C原子之间的伸缩振动.WC5团簇红外光谱有一个强振动峰位于振动频率最大2061.41cm-1处，红外光谱强度为1242.19km·mol-1，振动模式为C原子之间的伸缩振动；拉曼光谱中有两个较强的振动峰，最强振动峰位于1438.84cm-1处，拉曼活性为329.10A4·amu-1，振动模式为C 原子之间的伸缩振动.WC6团簇红外光谱有两个强振动峰，其余峰值较小，最强振动峰位于振动频率最大2091.22cm-1处，红外光谱强度为1639.85km·mol-1，振动模式为C 原子之间的伸缩振动；拉曼光谱中有两个较强的振动峰，最强振动峰位于1966.96 cm-1处，拉 曼 活 性 为1155.46 A4·amu-1，振动模式为C原子之间的伸缩振动.

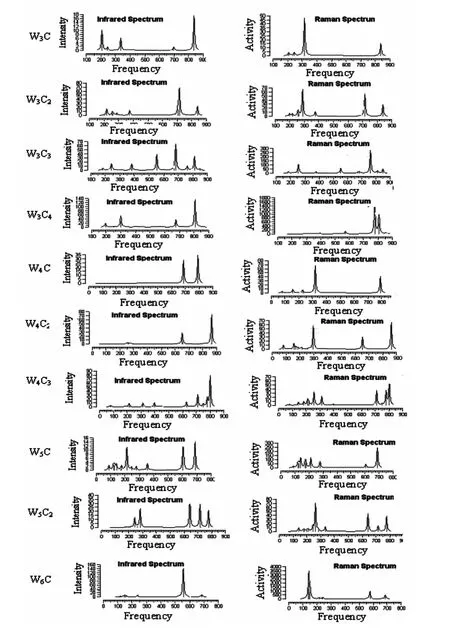
图2 WmCn（m+n≤7）团簇IR 光谱和Raman光谱Fig.2 Calculated IR and Raman spectra of WmCn（m+n≤7）clusters

对W2Cn（n≤5）团簇来说，W2C团簇红外光谱有一个最强振动峰，位于振动频率最大803.85 cm-1处，红外光谱强度为71.59km·mol-1，振动模式为C原子的伸缩振动；拉曼光谱中有两个较强的振动峰，最强振动峰位于803.85cm-1处，拉曼活性为62.88A4·amu-1，振动模式为C原子的摇摆振动，次强振动峰位于363.87cm-1处，拉曼活性为38.61A4·amu-1，振动模式为W 原子和C原子之间的伸缩振动，偶极距变化方向是垂直1W 原子和2W 原子的轴线方向.W2C2团簇红外光谱有两个较强振动峰，最强振动峰位于731.50cm-1处，红外光谱强度为47.36km·mol-1，振动模式为C原子摇摆运动，次强振动峰位于271.20cm-1处，红外光谱强度为31.45km·mol-1，振动模式为C原子的摇摆运动，在260.70cm-1、504.19cm-1、896.05cm-1处无红外活性，因为在其振动模式下团簇的偶极矩没发生变化；拉曼光谱中有一个较强振动峰，位于896.05cm-1处，拉曼活性为34.27 A4·amu-1，振动模式为C 原子的对称伸缩运动，在271.20cm-1、653.49cm-1、731.50cm-1处，无拉曼活性，因为在其振动模式下团簇的极化率变化极小.W2C3团簇红外光谱有三个较强振动峰，其最强振动峰位于764.73cm-1处，红外光谱强度为39.40km·mol-1，振动模式为C 原子沿W-W键轴线方向的伸缩振动；拉曼光谱中有五个明显的峰值，最强振动峰位于318.57cm-1处，拉曼活性为105.43A4·amu-1，振动模式为1C原子、5C原子的摇摆振动和W 原子的伸缩振动.W2C4团簇红外光谱最强振动峰位于213.99cm-1、处，红外光谱强度为139.76km·mol-1，振动模式为C 原子的摇摆振动，次强振动峰位于1355.02cm-1处，红外光谱强度为106.30km·mol-1处，振动模式为C原子在平面内的对称伸缩振动，在397.23cm-1至763.24cm-1范围内，无红外活性；拉曼光谱中有一个较强振动峰，位于1470.69cm-1处，拉曼活性为118.08A4·amu-1，振动模式为C 原子的伸缩振动.W2C5团簇红外光谱的最强振动峰位于最大频率1616.46cm-1处，红外光谱强度为93.65km·mol-1，振动模式为1C 原子、5C 原子的摇摆振动和2C 原子的对称伸缩振动；在最小频率265.90 cm-1和808.89cm-1之间存在多个振动峰，其中最强振动峰位于740.63cm-1处，红外光谱强度为52.81km·mol-1，振动模式3C 原子、4C 原子对称伸缩振动.拉曼光谱中有两个较强振动峰，最强振动峰位于715.18cm-1处，拉曼活性为57.44A4·amu-1，振动模式为1C原子及5C原子的伸缩振动.

对于W3Cn（n≤4）团簇，W3C团簇红外光谱有三个较强振动峰，最强振动峰位于838.90cm-1处，红外光谱强度为17.49km·mol-1，振动模式为C原子的伸缩振动；拉曼光谱中有两个较强振动峰，最强振动峰位于315.17cm-1处，拉曼活性为47.35A4·amu-1，振动模式为W 原子的伸缩振动.W3C2团簇红外光谱峰值较多，其中有两个较强振动峰，最强振动峰位于715.97cm-1处，红外光谱强度为67.85A4·amu-1，振动模式为3C 原子的伸缩振动，次强振动峰位于振动频率最大840.00cm-1处，红外光谱强度为22.80 A4·amu-1，振动模式为2C原子的伸缩振动，其余振动峰红外光谱强度较小；拉曼光谱中有三个较强振动峰，最强振动峰位于287.99cm-1处，拉曼活性为66.36A4·amu-1，振动模式为2C 原子摇摆振动与1W 原子的伸缩振动.W3C3团簇红外光谱振动峰较多，其中有三个较强的振动峰，最强振动峰位于683.32cm-1处，红外光谱强度为65.28km·mol-1，振动模式为C 原子的伸缩振动，次强振动峰位于553.05cm-1处，红外光谱强度为39.65km·mol-1，振动模式为C 原子的摇摆运动，较弱振动峰位于811.82cm-1处，红外光谱强度为34.28 km·mol-1，振动模式为2C 原子和3C 原子的摇摆振动，其余峰值较小，红外光谱强度未超过15.90 km·mol-1；拉曼光谱有三个较强振动峰，最强振动峰位于762.01cm-1处，拉曼活性为278.05A4·amu-1，振动模式为C原子的伸缩振动.W3C4团簇红外光谱中有三个较强振动峰，最强振动峰位于808.11cm-1处，红外光谱强为138.69 km·mol-1，振动模式为C 原子的相互伸缩振动；拉曼光谱中有两个较强振动峰，其最强振动峰位于778.43cm-1处，拉曼活性为1600.01A4·amu-1，振动模式为1C 原子、3C 原子、4C 原子的摇摆振动.

对W4Cn（n≤3）团簇来说，W4C团簇红外光谱有两个较强振动峰，最强振动峰位于791.92cm-1处，红外光谱强度为34.35km·mol-1，振动模式为C原子的伸缩振动；拉曼光谱有两个较强振动峰，最强振动峰位于319.80cm-1处，拉曼活性为70.51A4·amu-1，振动模式为1W 原子和3W 原子的伸缩振动，次强振动峰位于791.92cm-1处，拉曼活性为41.20A4·amu-1，振动模式为C原子的伸缩振动，其余拉曼活性不超过9.08 A4·amu-1.W4C2团簇红外光谱有两个较强振动峰，其最强振动峰位于865.55cm-1处，红外光谱强度为73.18km·mol-1，振动模式为C 原子的伸缩振动，次强振动峰位于652.16cm-1处，红外光谱强度为23.54km·mol-1，振动模式为C原子的摇摆振动，其余峰值较小；拉曼光谱有三个较强振动峰，其它拉曼活性较弱，最强振动峰位于862.54cm-1处，拉曼活性为66.15A4·amu-1，振动模式为C原子的伸缩振动.W4C3团簇红外光谱峰值较多，有两个较强振动峰，其余红外活性较弱，最强振动峰位于801.06cm-1处，红外光谱强度为78.32km·mol-1，振动模式为7C 原子、5C 原子的伸缩振动；拉曼光谱振动峰较多，有三个较强振动峰，分布在710.94cm-1和802.89cm-1范围内，最强振动峰位802.89 cm-1处，拉 曼 活 性 为61.94 A4·amu-1，振动模式为7C原子、5C 原子的伸缩振动；在78.32cm-1和396.47cm-1范围内分布了多个小振动峰，其中最强的位于257.00cm-1处，拉曼活性为32.87A4·amu-1.

对于W5Cn（n≤2）团簇，W5C团簇红外光谱有三个较强振动峰，最强振动峰位于689.08cm-1处，红外光谱强度为14.37km·mol-1，振动模式为C 原子的伸缩振动，而且在88.89cm-1和357.29cm-1范围内还分布了多个小振动峰；拉曼光谱有一个较强振动峰位于689.08cm-1处，拉曼活性为264.96A4·amu-1，振动模式为C 原子的伸缩振动，通过数据发现红外光谱最强锋和拉曼光谱最强锋都位于振动的频率的最大值689.08 cm-1处.W5C2团簇红外光谱有五个较强振动峰，最强振动峰位于642.04cm-1处，外光谱强度为36.18km·mol-1，振动模式为6C 原子的摇摆振动；拉曼光谱有三个较强振动峰，其余拉曼活性较弱，最强振动峰位261.37cm-1处，拉曼活性为70.59A4·amu-1，振动模式表现为整体的呼吸振动.

W6C团簇红外光谱最强振动峰位于556.01 cm-1处，红外光谱强度为146.98km·mol-1，振动模式为C 原子的摇摆振动；拉曼光谱最强振动峰位于142.47cm-1处，拉曼活性为3500.01A4·amu-1，振动模式表现C 原子和W 原子的整体伸缩振动.

通过WmCn（m+n≤7）团簇基态结构的光谱图可知，振动频率主要分布在55.99cm-1～2061.41cm-1之间，最强峰值的振动模式大部分为C原子或W 原子的伸缩振动，这是由于W-C 键存在较强的相互作用及团簇体系的电偶极矩变化较大的原因.在WmCn（m+n≤7）团簇中，对WCn（n≤6）团簇来说红外光谱的峰较少，是由于分子的振动自由度数目较少的原因，但红外光谱活性较强，振动模式均为沿轴线的伸缩振动，此振动模式改变了团簇结构中电子云的分布情况，导致了偶极矩的巨大变化，致使其红外活性高于其它团簇；除此之外对其它团簇来说红外光谱峰较多，但红外活性明显较弱且峰值变化范围不一，是因为振动形式不同对分子的电荷分布影响不同导致偶极矩变化不一，故峰值强度也不同；拉曼光谱的峰值变化范围不一，是由于极化率变化大小不同引起的.

4 结 论

采用密度泛函理论中的杂化密度泛函B3LYP方法在LANL2DZ基组水平上优化得到了WmCn（m+n≤7）团簇的基态结构，并对其振动光谱、自然键轨道进行了系统研究.结果表明：从基态构型看C原子对团簇的稳定性起到了主导作用，原子间趋于形成W-C键；从NBO 分析可知，在W 原子和C原子作用的过程中，W 原子的6s轨道上的电荷转移到了C原子2p轨道，产生了轨道杂化现象，易形成较强的化学键；振动光谱分析显示：最强峰值的振动模式大部分为C原子或W 原子的伸缩振动；振动频率主要分布在55.99cm-1～2061.41 cm-1之间.

［1］ Jiang G J，Zhuang H R，Li W L，et al.Produce tungsten carbides material from tungsten and carbon powers with different more ratios between them［J］.J.Mater.Sci.Eng.，2004，22（4）：471（in Chinese）［江国健，庄汉锐，李文兰，等.场激活加压合成燃烧合成碳化钨［J］.材料科学与工程学报，2004，22（4）：471］

［2］ Ma C N，Chen Z Y，Zhao F M.Synthesis of ultrafine mesoporous tungsten carbide by high ball milling and its electrocatalytic activity for methanol oxidation［J］.Chin.J.Chem.，2011，29（4）：611.

［3］ Zheng H J，Ma C，Huang J G，et al.Plasma enhanced chemical vapor deposition nanocrystalline tungsten carbide thin film and its electro-catalytic activity［J］.J.Mater.Sci.Tchnol.，2005，21 （4）：545.

［4］ You X Q，Song X F，Ren H，et al.Microstructure and wear properties of tungsten carbide reinforced steel matrix composites ［J］.Trans.Nonferrous Met.Soc.China，2005，15（6）：1332.

［5］ Zhou L Z，Meng X S，Li X M，et al.Investigation of the transition-carbon clusters ［J］.J.At.Mol.Phys.，2011，28（2）：287（in Chinese）［周留柱，孟祥省，李晓明，等.气象过渡金属坦-碳链团簇的研究［J］.原子与分子物理学报，2011，28（2）：287］

［6］ Mannesson K，Elfwing M，Kusoffsky A，et al.Analysis of WC grain growth during sintering using electron backscatter diffraction and image analysis［J］.Int.J.Refract.Met.Hard Mater.，2008，26（5）：449.

［7］ Peppernick S J，Gunaratne K D D，Castleman Jr.A W.Towards comprehending the superatomic state of matter［J］.Chem.Phys.Lett.，2010，489（1-3）：1.

［8］ Scharf T W，Romanes M C，Mahdak K C，et al.Atomic-scale structure and composition of tungsten carbide reinforced diamondlike carbon films［J］.Appl.Phys.Lett.，2008，93（15）：151909.

［9］ Zavodinsky V G.Small tungsten carbide nanoparticles：simulation of structure energetics and tensile strength［J］.Int.J.Refract.Met.Hard Mater.，2010，28（3）：446.

［10］ Tang G Y，Yang X.Geometry structures and stability ground of AlWN（N=1～9）clusters［J］.Phys.Exper.College，2007，20（4）：7（in Chinese）［唐国艳，杨雪.AlWn（n=1～9）团簇的结构与性质［J］.大学物理实验，2007，20（4）：7］

［11］ Zhang X R ，Li Y，Yang X.The theoretical study on structural and electronic properties of WnNim（n+m=8）clusters［J］.Acta Phys.Sin.，2011，60（10）：236（in Chinese）［张秀荣，李扬.WnNim（n+m=8）团簇结构与电子性质的理论研究［J］.物理学报，2011，60（10）：236］

［12］ Zhang X R，Liu X F，Kang Z L.The theoretical study on structure and optical spectrum of WnSi20，±（n=1～5）clusters ［J］.J.At.Mol.Phys.，2010，27（5）：869（in Chinese）［张秀荣，刘小芳，康张李.WnSi20，±（n=1～5）团簇结构与光谱的理论研究［J］.原子与分子物理学报，2010，27（5）：869］

［13］ Zhang X R，Gao C H，Wu L Q，et al.The theory study of electronic structures and spectrum properties of WnNim（m+n≤7；m=1，2）clusters［J］.Acta Phys.Sin.，2005，59（8）：248（in Chinese）［张秀荣，高从华，吴礼清，等.WnNim（m+n≤7；m=1，2）团簇电子结构与光谱性质的理论研究［J］.物理学报，2005，59（8）：248］

［14］ Zhang X R，Kang Z L，Guo W L.Electronic structure and infrared spectrum of a WnC0，±（n=1～6）cluster［J］.Chin.Phys.B，2011，20 （10）：103601.

［15］ Zhang X R，Ding X L，Yang J L.Density functional theory study of W5clusters ［J］.Int.J.Mod.Phys.B，2005，19（15）：2427.