Mg2Ni分子的结构和势能函数
洪文钦,胡爱荣,阮 文
(1.南昌大学理学院,南昌 330031;2.井冈山大学数理学院,吉安343009)
1 引 言
镁基储氢材料以吸氢量大、资源丰富、价格低廉、质量轻和无污染而被认为是最有发展前途的固态储氢材料,引起了研究者的广泛关注.如,早在1968 年美国布鲁克海文国家实验室Reilly 和Wiswall[1]以镁和镍混合熔炼合成了Mg2Ni合金,并指出Mg2Ni在一定的温度和压强下与氢气反应生成Mg2NiH4,得到Mg2Ni储氢材料的理论储氢量为3.6%;1987年Ivanov等[2]成功利用机械合金法制备了Mg2Ni;Kohno等研究得到Mg2Ni镁基储氢材料的电化学最大放电容量为999mAh/g[3],可作为电池的理想负极材料.随着各种制备方法的出现,镁基储氢材料的研究取得快速发展,人们对其各种特性进行了大量研究[4-12].但是,目前表明对于Mg2Ni的研究仅仅限于其储氢性能和循环利用等,尚没有对Mg2Ni的结构及其势能函数进行深入研究.分子势能函数是分子电子能量的完全描述,不仅是原子分子物理学和材料科学的重要基础,而且还是研究原子与分子碰撞和分子反应动力学的关键.深入研究Mg2Ni的结构及其势能函数对于理解其与氢分子的反应动力学及其储氢性能具有积极的意义.本文采用密度泛函(DFT)理论B3LYP 方法对MgNi、Mg2和Mg2Ni进行理论计算,得到了MgNi、Mg2和Mg2Ni的几何结构和解析势能函数,对于理解Ni+ Mg2反应机理具有重要的参考价值.
2 理论计算
使用6-311+G(d,p)全电子基组,采用密度泛函B3LYP 方法,对Mg2、MgNi分子和Mg2Ni分子的各种可能构型进行优化,得到了Mg2、Mg-Ni和Mg2Ni分子的基态几何结构.Mg2的平衡核间距为0.3939nm,能量为-400.18706a.u,其核间距与罗友华等的理论计算值(0.3502nm)[13]和实验值(0.3891nm)[14]符合较好;MgNi分子的平衡核间距为0.2519 nm,与理论值(0.2513 nm)[13]也符合较好,能量为-1708.37141a.u.;线性Mg-Ni-Mg(D∞h)分子的平衡核间距RMgNi=0.2633nm,能量为-1908.48209a.u.;而线性Ni-Mg-Mg的能量为-1908.47240a.u,角型C2v的能量为-1908.48206a.u..所以,Mg2Ni分子的基态构型为Mg-Ni-Mg(D∞h),电子状态为三重态,其平衡核间距RMgNi与盛勇等[15]的理论值(0.2608nm)一致,能量与张秀荣等[16]的理论值(-1908.479a.u)也是一致的,说明本文选用的方法是合适的.同时本文还计算了线性Mg2Ni分子(D∞h)基态的简正振动频率:弯曲振动频率ν1=39.2964cm-1、对称伸缩振动频率ν2=172.7969 cm-1、反对称伸缩振动频率ν3=190.9285cm-1.全部计算采用Gaussian03[17]程序.
2.1 MgNi分子和Mg2Ni分子离解极限
计算得到MgNi分子基电子状态为(X3Δ),根据原子分子反应静力学基本原理[18],基态MgNi分子的离解极限为:

计算得到Mg2Ni分子的轨道排布:
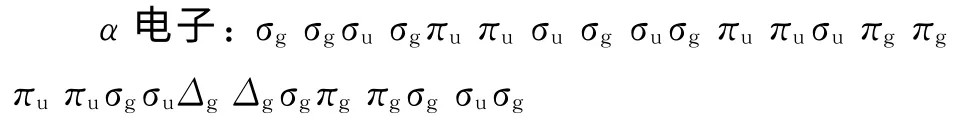

根据轨道能量大小配对后,最外层分子轨道Δgσg,两者直积为3Δg,即Mg2Ni分子的基态电子状态为3Δg.其离解通道由下式构成:


2.2 MgNi和Mg2分子基态的分析势能函数
采用B3LYP/6-311+G(d,p)方法对MgNi和Mg2分子的几何构型优化完成后,对基态进行单点能计算,键长范围为1.5Å~9.0Å,步长为0.1Å,得到的一系列单点势能值,采用最小二乘法拟合为Murrell-Sorbie(M-S)势能函数[19-21].

式中:ρ=r-re,r、re分别为核间距和平衡核间距,De、a1、a2、a3为(M-S)拟合参数,结果列于表1.
同时,基于M-S势能函数(2),根据参数ai和De与力常数和光谱数据的关系[19-22],得到MgNi和Mg2分子基态的二阶、三阶及四阶力常数和光谱常数,结果列于表2.
表2中f2、f3和f4分别为二阶、三阶及四阶力常数,ωe为谐振频率,χe为非谐振动因子,Be、αe为刚性和非刚性转动因子.
图1和图2是相应的势能曲线,图中离散点为计算点,实线为拟合出的势能曲线,两者在全范围内是一致的.图1~2 和表1 可见MgNi和Mg2分子的离解能均很小,特别是Mg2分子的离解能仅为0.0288eV,可见Mg2分子中的Mg原子之间通过范德瓦耳斯键发生相互作用.

表1 MgNi和Mg2分子Murrell-Sorbie势能函数参数Table 1 The M-S potential energy functional parameters for MgNi and Mg2 molecules

表2 MgNi和Mg2分子的力常数和光谱常数Table 2 The force constants and spectrum datum for MgNi and Mg2 molecules

图1 基态Mg2分子(X1Σg)势能曲线Fig.1 The potential energy curve of Mg2(X1Σg)

图2 基态MgNi分子(X3Δ)势能曲线Fig.2 The potential energy curve of MgNi(X 3Δ)
2.3 Mg2Ni分子多体项展式的势能函数

基于式(1)的离解极限,Mg2Ni体系的多体项展式的势能函数解析式为:取基态原子的能量作为能量零点,式中的双体项采用M-S势能函数(2),MgNi和Mg2分子的两体项数据见表1、2;对三体项,选择Mg-R1-Ni-R2-Mg 作为参考结构,(R01=R02=0.2633 nm,R03=R01+R02=0.5266nm)作为参考坐标,则内坐标ρi 及相应的对称内坐标为:

(3)中的V(3)MgNiMg(R1,R2,R3)为三体项,采用的形式为

式(4)中P 为对称内坐标Si的多项式,T 为量程函数,它们的形式为:

在(5)、(6)中,有五个线性系数(C1,C2,C3C4,C5)和两个非线性系数(γ1,γ3),对势能面进行非线性优化,确定两个非线性系数;而五个线性系数可由表3所列已知条件拟合确定,三体项参数可由此而确定,结果列于表4.
势能函数(3)的等值势能图如图3和图4,这两个图正确复现了Mg2Ni(~X3Δg)的平衡结构特征.在图3 中固定∠MgNiMg=180°,此图表示了Ni-Mg键对称伸缩振动的等值势能面.从图中发现,由Mg+MgNi生成Mg2Ni(D∞h)分子在R1=R2=0.2633nm 处存在一个势阱(-1.22 eV),准确再现了Mg2Ni(D∞h)分子的离解能1.2283eV,并且可以看到反应过程中不存在任何鞍点.因此,Mg+ MgNi生成Mg2Ni(D∞h)分子是一个无阈能的放热反应,反应比较容易进行.

表3 基态Mg2Ni的结构与性质参数Table 3 Structure and property parameters of Mg2Ni molecule

表4 基态Mg2Ni分析势能函数三体项的参数Table 4 Coefficients of 3-body term of potential energy function for Mg2Ni

图3 Mg2Ni分子的伸缩振动等值势能面Fig.3 The stretch potential energy surface of Mg2Ni
图4中固定RMgMg为0.5266nm,让Ni原子绕Mg-Mg转动的等值势能面.图中清晰地显示了Mg2Ni(~X3Δg)分子的平衡结构特征:有一个线性极小点,即当Ni原子位于(X =0.0nm,Y =0.0nm)时存在一势阱(-1.20eV),再一次吻合了Mg2Ni(D∞h)分子的优化结果及分子的离解能1.2283eV.图4 中还存在一个C2V构型的鞍点(X =±0.0nm,Y =0.20nm),这说明Ni原子垂直于Mg-Mg键进攻时,存在一定的势垒,只有当Ni原子具有一定的活化能,才可能破坏Mg-Mg键而生成Mg-Ni-Mg分子.如果Ni原子以此方向进攻Mg-Mg键,大约需要的活化能为ΔH =0.1eV(9.6567kJ),因此说明Ni原子与Mg-Mg反应时,需要克服一定的能垒才能形成稳定的Mg2Ni(~X3Δg)分子.
3 结 论

图4 Mg2Ni分子的旋转等值势能面Fig.4 The rotational potential energy surface of Mg2Ni
本文采用密度泛函(DFT)理论B3LYP 方法对MgNi、Mg2和Mg2Ni进行理论计算,在优化Mg2Ni稳定构型和平衡几何基础上,确定了Mg2Ni(~X3Δg)正确的离解极限和离解能.获得了Mg2Ni(~X3Δg)分子的势能值和二阶力常数.在此基础上,应用多体项展式理论得到了Mg2Ni(~X3Δg)的解析势能函数,其等值势能面正确反应了Mg2Ni(~X3Δg)的平衡结构特征,以及Mg+MgNi→MgNiMg和Ni+Mg2→MgNiMg的反应动力学特点,为进一步研究Mg2Ni的碰撞及储氢性能等微观反应机理奠定基础.
[1] Reilly J J,Wiswall R H.The reaction of hydrogen with alloy of magnesium and nickel and the formation of Mg2NiH4[J].Inorg.Chem.,1968,7:2254.
[2] Ivanov E,Konstanchuk I,Stepanov A,et al.Magnesium mechanical alloys for hydrogen storage[J].J.Less Common Met.,1987,131:25.
[3] Kohno T,Yamamoto M,Kanda M.Electrochemi-cal properties of mechanically ground Mg2Ni alloy[J].J.Alloys Compd.,1999,293-295:643.
[4] Jasen P V,González E A,Brizuela G,et al.A theoretical study of the electronic structure and bonding of the monoclinic phase of Mg2NiH4[J].Int.,J.Hydrogen Energy,2007,32:4943.
[5] Chen X J,Xia T D,Liu X L,et al.Mechanism of combustion synthesis of Mg2Ni[J].J.Alloys Compd.,2006,426:123.
[6] Liu X F,Zhu Y F,Li L Q.Structure and hydrogenation properties of nanocrystalline Mg2Ni prepared by hydriding combustion synthesis and mechanical milling[J].J.Alloys Compd.,2008,455:197.
[7] Ma S Y,Huang D,Zheng D S,et al.First principles calculation on Mg2Ni alloy and its hydride electronic structure and bond characteristics[J].The Chinese Journal of Nonferrous Metals,2007,17:118(in Chinese)[马树元,黄丹,郑定山,等.Mg2Ni合金及其氢化物的电子结构及成键特性的第一原理计算[J].中国有色金属学报,2007,17(1):118]
[8] Lei Q H,Chen C A,Xiong Y F.Thermodynamic hydrogen lsotopic effect of Mg2NiQ6(Q=H,D,T)[J].Acta Phys.Chim.Sin.,2009,25:941.(in Chinese)[雷强华,陈长安,熊义富.Mg2NiQ6(Q=H,D,T)体系的热力学氢同位素效应[J].物理化学学报,2009,25:941]
[9] Li G X,Chen X W,Bai J D,et al.Adsorption and diffusion of Hon Mg2Ni(100)Surface[J].Acta Phys.Chim.Sin.,2010,26:1448(in Chinese)[黎光旭,陈晓伟,白加栋,等.氢在Mg2Ni(100)面的吸附及扩散[J].物理化学学报,2010,26:1448]
[10] Xiao R J,Guo J,Zhou J,et al.Adsorption and dissociation of H2on Mg2Ni(010)surface[J].J.At.Mol.Phys.,2012,29:523(in Chinese)[肖荣军,郭进,周江,等.氢在Mg2Ni(010)面的吸附及分解[J].原子与分子物理学报,2012,29:523]
[11] Li W Y,Li C S,Ma H,et al.Magnesium nanowires:enhanced kinetics for hydrogen absorption and desorption[J].Am.Chem.Soc,2007,129:6710.
[12] Zlusk A A,Zaluski L,Stromclsen J O.Synergy of hydrogen sorption in ball-milled hydrides of Mg and Mg2Ni[J].J.Alloys Compd.,1999,289:197.
[13] Yao J G,Wang X W,Luo Y H,et al.First-principles study of the NiMgn(n=1~12)clusters[J].Acta Phys.Sin.,2008,57:4166(in Chinese)[姚建刚,王献伟,罗有华,等.NiMgn(n=1~12)团簇的第一性原理研究[J].物理学报,2008,57:4166]
[14] Ruette F,Sanchez M,Anez R,et al.Diatomic molecule data for parametric methods[J].J.Mol.Struct.:Theochem,2005,729:19.
[15] Chen X F,Zhu Z H,Sheng Y,et al.Density functional theory study on Ni-doped MgnNi(n=1~7)clusters[J].Chin.Phys.B,2010,19:033601.
[16] Zhang X R,Gao C H.Geometrical structures and spectrum properties of MgxNiy(x=1,2;y=1~5)clusters[J].Journal of Jiangsu University of Science and Technology(Natural Science Edition),2010,24:309 (in Chinese)[张 秀 荣,高 从 花.MgxNiy(x=1,2;y=1~5)团簇结构与光谱性质的理论研究[J].江苏科技大学学报:自然科学版,2010,24:309]
[17] Frisch M J,Trucks G W,Schlegel H B,et al.Gaussian 03,revision C.02 wallingford C T:gaussian,Inc,2004.
[18] Zhu Z H.Atomic and molecular reaction statics[M].Beijing:Science Press,1996(in Chinese)[朱正和.原子分子反应静力学[M].北京:科学出版社,1996]
[19] Zhu Z H,Yu H G.Molecular structure and molecular potential energy function[M].Beijing:Science Press,1997(in Chinese)[朱正和,俞华根.分子结构与分子势能函数[M].北京:科学出版社,1997]
[20] Ruan W,Luo W L,Zhang L,et al.The molecular structure and analytical potential energy function of TiH2(~X3A2)[J].J.At.Mol.Phys,2008,25:767(in Chinese)[阮文,罗文浪,张莉,等.TiH2分子结构与势能函数[J].原子与分子物理学报,2008,25:767].
[21] Ruan W,Hu Q L,Xie A D,et al.The molecule structure and potential energy function of NiCO[J].J At.Mol.Phys.,2010,27:215(in Chinese)[阮文,胡强林,谢安东,等.NiCO 分子结构与解析势能函数[J].原子与分子物理学报,2010,27:215]
[22] Zhao Q,Liu F L,Zhou L S,et al.Structures and potential energy functions of La2and LanF(n=1~2)molecules[J].J.At.Mol.Phys.,2013,30:59(in Chinese)[赵倩,刘凤丽,周凌松,等.La2与LanF(n=1~2)分子的结构与势能函数[J].原子与分子物理学报,2013,30:59]
——《势能》

