对接双材平面中圆弧裂纹问题的数值方法

杜云海， 刘雯雯， 徐轶洋

(郑州大学力学与工程科学学院 河南郑州450001)

0 引言

在工程结构中出现的裂纹往往呈曲线形状，特别是大尺度裂纹，理想的直线状裂纹是极少见的．圆弧作为一般曲线的极好近似，以此建立裂纹尖端应力强度因子的数值方法，对于工程实际中曲线裂纹问题的实用计算具有重要意义．关于圆弧裂纹问题，文［1－2］曾研究过有限元法，文［3］曾研究过复变函数半逆解法，文［4］则研究了边界元法．超奇异积分方程法作为一种能快速求解裂纹问题的半数值方法，近年来也受到诸多学者关注［5－7］，作者在这方面也曾做过一些探索［8－10］，并在近期研究了双材料平面中的一般曲线裂纹问题．本文基于研究所得精确描述圆弧裂纹问题的超奇异积分方程组，建立相应的数值方法，并对应力强度因子(SIF)进行了系统的计算．

1 超奇异积分方程组

假定双材料平面中有一条圆弧裂纹，如图1所示，Gi、μi(i=1，2)分别为两半平面材料的切变模量与泊松比，裂纹长度为2a，裂纹半径为R，裂纹中点坐标为(c，d)，中点半径与横轴之间的夹角为θ0，则裂纹曲线的参数方程可表示为

其中，s为裂纹的弧长坐标．

若仅在裂纹岸上作用大小相等、方向相反的分布载荷qj(s)(j=1，2;－a＜s＜a)，则问题的应力边界条件为

利用互等功定理可得到上述问题用弹性力学基本解表达的位移场，然后再利用几何方程、物理方程和边界条件(2)，经过严格数学推导，将具有奇异性的项合并后再从结果中分离出非奇异部分，可得到描述该问题的超奇异积分方程组

图1 双材料平面中的圆弧裂纹Fig．1 An arc crack in bi-material plane

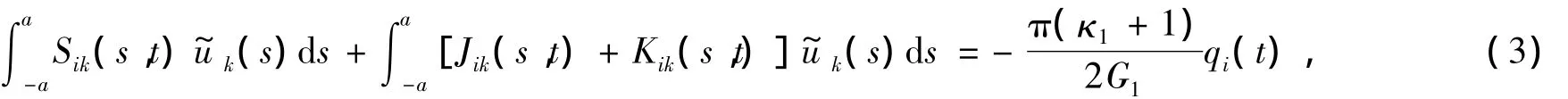
这里S12(s，t)、S21(s，t)为奇异积分核函数的曲率影响项;Jik(s，t)为正常积分核函数的曲率影响项，可写成幂级数形式:

其中Bj为伯努利数(可查数学手册);而Kik(s，t)为一般正常积分核函数(无奇异性，限于篇幅不再给出);对于平面应力问题，式(3)中的κi=(3－μi)/(1+μi);而对于平面应变问题，κi=(3－4μi)．不难看出，S12，S21，J11，J22，J12，J21等曲率影响项都随圆弧裂纹半径R的增大而减小，当R→∞ 时，式(3)退化为直线裂纹问题的超奇异积分方程组，与文［8］结果一致．

2 数值方法

为建立应力强度因子的数值算法，需将式(3)进行归一化处理，这里引入如下变量与函数替换

将式(6)代入式(3)，可得到归一化超奇异积分方程组为

归一化方程组(7)形式上与文［10］结果相同，因此其后继处理可参照文［10］，将裂纹位移间断fk(ζ)用含契比谢夫多项式的配置函数表示，并利用已有奇异积分的有限分部积分结果［7］，适当增配方程个数，可将问题转化为一个封闭可解线性方程组的建立，应力强度因子则可用方程组的解(即契比谢夫多项式的系数)来表示．

利用上述方法，通过适当编程即可实现该问题无量纲应力强度因子的快速计算．通过增加配置方程数重新计算，并与上次结果相比较，可有效控制应力强度因子的计算精度．本文实际应用程序的控制计算精度为5×10－4．

3 圆弧裂纹的应力强度因子(SIF)

假定对接双材料平面中一条圆弧裂纹在裂纹岸上仅承受均布压力q0，选择不同的圆弧中点坐标c/a、不同半径R/a和切变模量比G2/G1，当裂纹中点的半径与水平坐标轴之间的夹角取不同值(0°、45°和90°)时，无量纲应力强度因子的计算结果如表1～3所示．这里，是圆弧裂纹尖端应力强度因子与距界面无限远处直线裂纹的应力强度因子之比．

计算结果表明，在单纯法向载荷作用下，对于均质材料(G2/G1=1)，圆弧裂纹的半径越小，Ⅰ型应力强度因子越小，并伴随着Ⅱ型应力强度因子的增大，其量级较小，所以非直线裂纹与直线裂纹相比是有利的．而对于双材料(G2/G1≠1)，圆弧裂纹半径的变小导致应力强度因子的变化较复杂，其变化规律与裂纹的方位有关．在距离界面较远处，变化规律如同均质材料，但在靠近界面处，会出现随着圆弧半径变小而Ⅰ型应力强度因子反而变大，Ⅱ型应力强度因子有时变大、有时变小的情况，如表1中c/a=1的结果所示，但多数情况下还是遵从与均质材料相同的规律．因此，总体来说，材料中的非直线裂纹较直线裂纹安全．此外，材料的切变模量比也是影响应力强度因子大小的主要因素，在G2/G1＜1时导致Ⅰ型应力强度因子变大，而在G2/G1＞1情况下，导致Ⅰ型应力强度因子变小，这种变化应归因于半平面之间的相互约束．

表1 圆弧裂纹中点径向角θ0=0°时的无量纲应力强度因子Tab．1 Dimensionless SIFs when midpoint radial angle of circular crack was θ0=0°

表2 圆弧裂纹中点径向角θ0=45°时的无量纲应力强度因子Tab．2 Dimensionless SIFs when midpoint radial angle of circular crack was θ0=45°

表3 圆弧裂纹中点径向角θ0=90°时的无量纲应力强度因子Tab．3 Dimensionless SIFs when midpoint radial angle of circular crack was θ0=90°

4 结论

基于所得圆弧裂纹问题的超奇异积分方程，通过变量与函数代换进行归一化处理，建立了该问题的数值方法，并通过进一步编程计算，系统求解了双材料平面中圆弧裂纹问题的无量纲应力强度因子．结果表明，虽然在裂纹岸作用单一法向载荷，因裂纹变曲却使得Ⅰ、Ⅱ型应力强度因子同时存在，但Ⅱ型应力强度因子量级较小，与无限远处直线裂纹相比，应力强度因子的变化一般呈减小趋势;而在双材料界面附近，应力强度因子的变化规律较为复杂，表现为有时变小，有时增大，这主要取决于裂纹的方位．另一方面，当含裂纹半平面的切变模量大于另半平面的切变模量时，裂纹越靠近界面，Ⅰ型应力强度因子越大;相反情况下，裂纹越靠近界面，Ⅰ型应力强度因子越小;量级较小的Ⅱ型应力强度因子一般也呈相同变化规律，但有时则呈相反的变化，这也取决于裂纹的方位;当裂纹远离界面时，界面对应力强度因子大小的影响消失．

［1］ Heitzer J，Mattheck C．Fem-calculation of the stress intensity factors of a circular arc crack under uniaxial tension［J］．Engineering Fracture Mechanics，1989，33(1):91 －104．

［2］ Lorentzon M，Eriksson K．A path independent integral for the crack extension force of the circular arc crack［J］．Engineering Fracture Mechanics，2000，66(5):423 －439．

［3］ Shen Dawei，Fan Tianyou．Semi-inverse method for solving circular arc crack problems［J］．Engineering Fracture Mechanics，2004，71(12):1705－1724．

［4］ Yan Xiangqiao．A boundary element analysis intensity factors of multiple circular arc cracks in a plane elasticity plate［J］．Applied Mathematical Modelling，2010，34(10):2722 －2737．

［5］ Ioakimids N I．A natural approach to the introduction of finite-part integrals into crack problems of 3-dimensional elasticity［J］．Engng Fract Mech，1982，16(5):669 －673．

［6］ Ioakimids N I．Application of finite-part integrals to the singular integral equations of crack problems in plane and 3-dimensional elasticity［J］．Acta Mech，1982，45(1/2):31 －47．

［7］ Chan Younsha，Fannjiang A C，Paulino G H．Intergral equations with hypersingular kernels-theory and applications to fracture mechanics［J］．International Journal of Engineering Science，2003，41(7):683 －720．

［8］ 杜云海，乐金朝．双材料平面中斜裂纹问题的超奇异积分方程方法［J］．机械强度，2004，26(3):326－331．

［9］ 乐金朝，杜云海，万强，等．双材料平面多裂纹问题的超奇异积分方程方法［J］．岩石力学与工程学报，2004，23(22):3834－3839．

［10］杜云海，吕存静，董栋，等．环形界面双材平面中环向裂纹问题的超奇异积分方程法［J］．机械强度2006，28(5):733－738．