改进的一比特量化压缩感知重建算法*
党 骙,马林华,田 雨,孙玉雪,茹 乐
(1.空军工程大学 航空航天工程学院,西安710038;2. 西安电子科技大学 综合业务网理论及关键技术国家重点实验室,西安710071;3.空军工程大学 信息与导航学院,西安710077)
1 引 言
压缩感知理论指出,通过适当的方法,稀疏信号或可压缩信号可以从其线性欠采样测量中精确重建出来[1-2]。目前大多数的研究所考虑的测量值都是实值的,具有无限比特精度。然而,在实际处理中,需要将采集到的测量值进行量化,以确保能够将数据进行存储和传输,即将实值测量值映射为有限域上的离散值[3]。例如,在均匀量化中,将测量值量化至2B个离散值,B 表示量化比特数。量化是不可逆的,在量化过程中会引入量化误差,通常将量化误差看作加性噪声来处理。近年来,一些学者研究了测量值的量化问题,并提出了相关重建方法[4-5]。
Boufounos 和Baraniuk 在文献[6]中指出,将测量值用一个比特表示,即只保留测量值的符号,仍然可以精确稳定地重建原始信号。采用这种量化方式可以大大降低信号在传输和存储过程中的比特数,在多数情况下,目标是减少总的比特数和非测量数。并且在许多情况下,量化消耗远大于采样消耗,而1-bit 压缩感知在量化过程中只需要一个比较器就可以实现高速稳定的量化。
目前,基于1-bit 压缩感知的重建算法主要有符号匹配追踪算法(Matching Sign Pursuit,MSP)[7]、约束步长收缩算法(Restricted- step Shrinkage,RSS)[8]、二进制迭代硬阀值算法(BIHT)[9]等,其中BIHT 算法比其他算法在重建精度和重建一致性上都要高。
本文正是在BIHT 算法的基础上,在每一步迭代过程中引入回溯[10]筛选的步骤,提出了基于回溯的二进制迭代硬阀值算法(BBIHT),该算法在每次迭代过程中,将前后两次迭代的支撑集合并,再在合并的支撑集下一致性重建。回溯步骤的加入优化了迭代过程中支撑的选择,避免了同一原子在前后两次迭代中被反复筛选和删除,降低了算法的重建复杂度。实验仿真表明,在较低采样比特数下,BBIHT算法比BIHT 算法重建精度要高,重建速度要快。
2 1-bit 压缩感知理论

1-bit 压缩感知是考虑对测量值量化的一种极限情况,表示为

其中,sign(·)表示符号函数,当测量值为正时取值为+1 否则为-1;M 表示测量值的数目,而在1-bit 量化中,测量数即比特数。为了得到更高的重建精度,可以增加M 值的大小,甚至可以大于信号长度N。
一致性重建定义[11]如下:

其中,Y=diag(y),即量化后的测量值构成的对角矩阵。
由于1-bit 量化使得信号幅度信息丢失,因此对信号增加一个能量约束,使重构信号在单位超球面上:
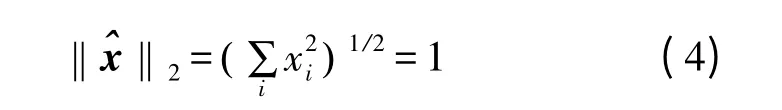
这一约束使得求解空间缩小,提高了重建精度。
3 算法设计
3.1 二进制迭代硬阀值算法
为了从1-bit 测量中重建出原始信号,文献[9]给出BIHT 算法所求解问题为
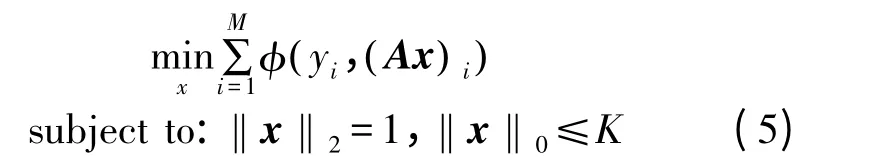
其中,
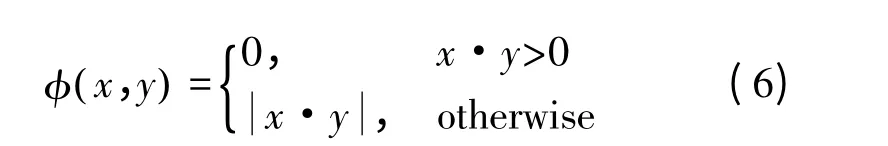
BIHT 算法步骤如下:
步骤1:初始化,最大迭代次数nmax,迭代次数n=0,x0=0,稀疏度K;
步骤3:计算xn+1=ηKan+1(),并令n=n+1;
步骤4:当n = nmax或y-sign(x)= 0 时输出xn+1/‖xn+1‖,否则转步骤2。
其中,μ为标量,用来控制梯度下降步长的大小,函数ηK( v)用来保留v 中最大的K 个量并将其余量置零。
3.2 基于回溯的二进制迭代硬阀值算法
本文受到文献[10]中对支撑进行回溯筛选的启发,将回溯的方法引入BIHT 算法中,在每次迭代过程中,将前后两次迭代的支撑进行合并,并在该支撑下一致性重建,即在该支撑下最小化
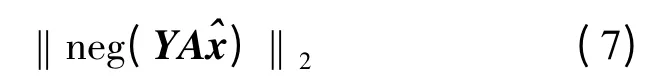
BBIHT 具体算法步骤如下:
步骤1:初始化,最大迭代次数nmax,迭代次数n=0,x0=0,稀疏度K;
步骤3:计算cn+1=ηK(an+1),合并前后两次迭代支撑Γn=supp(cn+1)∪supp(xn);
总而言之,农村气象服务建设作为一项长期性、系统性、复杂性工程,必须投入更多人力、物力、财力,全面提升农村气象的整体服务水平。加大气象服务工程建设力度,为有效预防和处理农业灾害、增加农民收入和农作物产量发挥出不可取代的作用。此外,农村气象服务是新农村重点建设内容,对于社会进步和国家繁荣发展等目标实现提供了有力条件。
步骤4:在支撑集下一致性重建
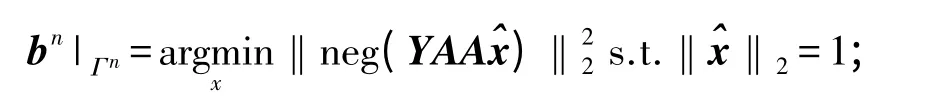
步骤5:当n=nmax或‖neg(YA)‖2=0 时,输出xn+1=bn|K/‖bn|K‖2,否则转步骤2。
通过对比研究BIHT 算法和BBIHT 算法发现,在BIHT 算法迭代过程中,不断将信号残差投影到测量矩阵A 列构成的原子库中最匹配的K 个原子,确定K 个可信赖的候选,当认为所选列是可信赖的,则将其加入下一次迭代序列。由于这种方式缺乏A 各列之间的正交性而不是最优的,向量a 的某个支撑可能由于不在信赖候选集内而被丢弃,但是在下一次的迭代中又因为加入残差投影,又被选入到可信赖的支撑集内,因此可能产生a 的某个支撑被反复丢弃和保留,从而导致整个算法需要迭代较多次数才能达到较高重建精度。
而BBIHT 算法通过加入回溯步骤,使同一原子被反复选择和丢弃的概率大大降低,通过在合并的支撑上一致性重建,提高了信号的重建精度和重建速度。本文算法所用思想与文献[10]中基本相同,然而算法实现时文献[10]采用最小二乘的方式,而本文算法是根据一致性原理进行重建,且两种算法针对问题不同,本文算法是考虑量化情况下的重建算法,因此也更加具有实际中的存储传输意义。
4 实验仿真及分析
在文献[9]中BIHT 算法已经与其他算法进行了对比,因此本文只用BBIHT 算法与BIHT 算法进行对比,并且设定与该文献相同的实验条件。原始待采样信号x 长度为N,稀疏度为K 且非零值在单位球上随机取值,即满足‖x‖2=1,测量矩阵A 采用大小为M×N 的高斯随机测量矩阵。定义重构误差为,角度误差(Angular Error)为arccos〈x,〉/π,且均为1 000次实验的平均值。
设定信号长度N=1 000,稀疏度K=10,采样率M/N 在区间[0,2]上取值(当M/N>1 时所获得测量值将大于原始信号的长度,这在传统的压缩感知中是不存在的,然而在1-bit 压缩感知中关注的是总的比特数而非测量值数,因此M/N>1 的情况在1-bit压缩感知中是常见的)所得BBIHT 与BIHT 重构误差比对如图1所示,重建时间比对如图2所示,角度误差比对如图3所示。
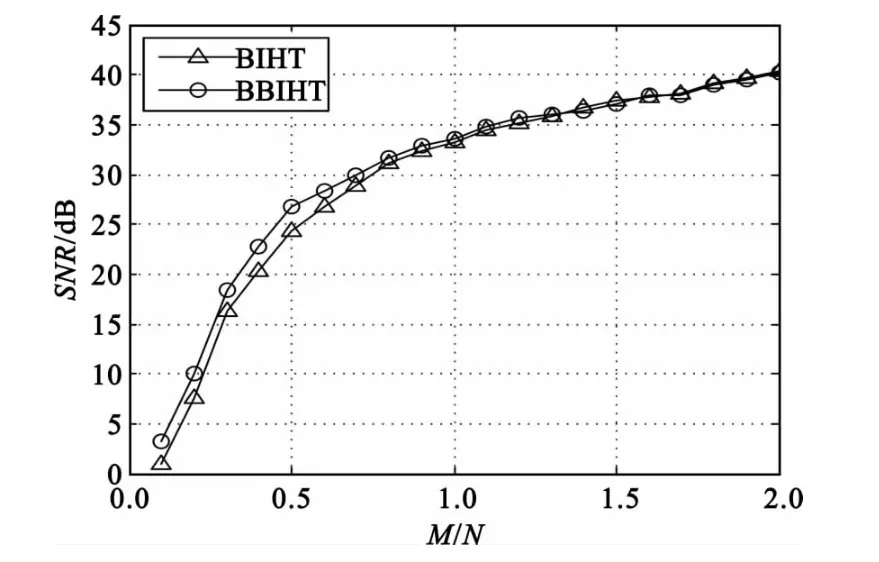
图1 BBIHT 与BIHT 重建误差比对Fig.1 Reconstruction error between BBIHT and BIHT
由图1可以看出,采样率在0.7 以下时,BBIHT的重建精度比BIHT 的要高约2~3 dB,在大于0.7时两种算法的重建精度基本趋于相同,采样率大于1.2 时两者的重建精度基本一致。
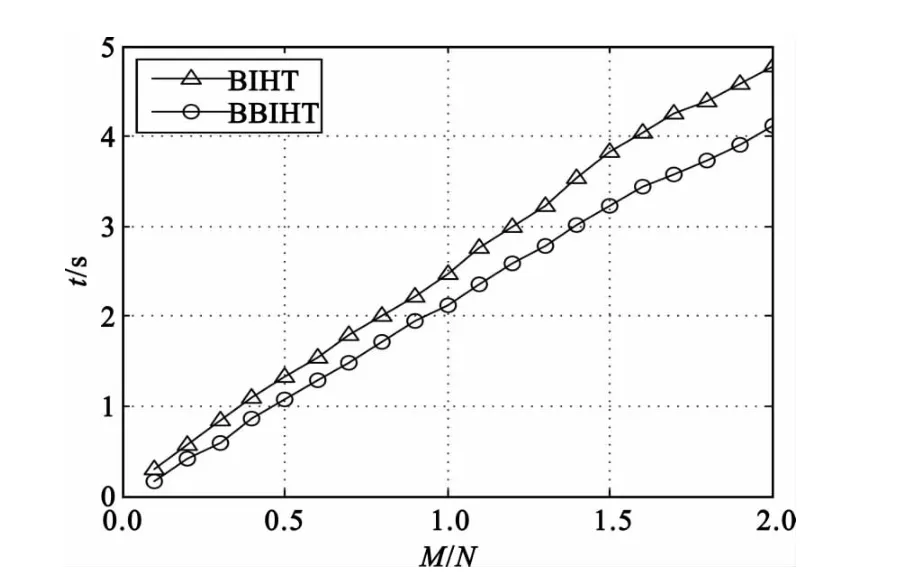
图2 BBIHT 与BIHT 重建时间比对Fig.2 Reconstruction time between BBIHT and BIHT
从图2时间曲线可以看出,在相同条件下BBIHT 算法的重建速度要高于BIHT 算法;两者时间开销大致随着采样率的增加呈线性升高趋势,且BIHT 算法的重建时间曲线斜率略大于BBIHT 算法时间曲线,因而随着采样率增加,BBIHT 算法的时间开销增长速度略慢于BBIHT 算法。

图3 BBIHT 与BIHT 重建角度误差比对Fig.3 Reconstruction angular error between BBIHT and BIHT
由图3可以看出,在采样率小于0.6 时,采用BBIHT 算法重建信号所得角度误差稍小于BIHT 算法,当采样率大于0.6 时,两者的重建角度误差基本相同,说明了本文所提算法的重建一致性要高于BIHT 算法。
5 结 论
本文对BIHT 算法迭代过程中可能产生原子被反复筛选和丢弃的情况进行分析,并通过引入原子的回溯筛选思想,提出了基于回溯的BIHT 算法。通过这种方法,大大降低了同一原子在前后两次迭代过程中被反复筛选和删除的概率,降低了算法的重建复杂度。通过仿真实验可以看出,本文所提算法在采样率较低时(低于0.7)的重建精度比BIHT算法高出约2~3 dB,达到重建精度所需时间略低于BIHT 算法,重建一致性也高于BIHT 算法,说明本文算法比BIHT 算法更具有实际应用意义。本文实验结果均是通过大量样本得到的平均值,实验中并无例外情况。下一步还应更加深入地进行数学分析,使算法在理论上更加完善。
[1] 邵文泽,韦志辉. 压缩感知基本理论:回顾与展望[J].中国图像图形学报,2012,17(1):1-12.SHAO Wen-ze,WEI Zhi-hui. Advances and perspectives on compressed sensing theory[J]. Journal of Image and Graphics,2012,17(1):1-12.(in Chinese)
[2] 乔田田,张宇,李维国.一种基于压缩感知的信号重建新算法[J].电讯技术,2013,53(10):1289-1292.QIAO Tian-tian,ZHANG Yu,LI Wei-guo. A New Signal Reconstruction Algorithm Based on Compressed Sensing[J]. Telecommunication Engineering,2013,53(10):1289-1292.(in Chinese)
[3] Boufounos P T,Jacques L. Quantization and Compressive Sensing[EB/OL]. [2014-05-07]. http://arxiv.org/abs/1405.1194.
[4] Zymnis A,Boyd S,Candes E.Compressed sensing with quantized measurements [J]. IEEE Signal Processing Letters,2010,17(2):149-152.
[5] Laska J N,Boufounos P T,Davenport M A,et al. Democracy in action:Quantization,saturation,and compressive sensing[J]. Applied and Computational Harmonic Analysis,2011,31(3):429-443.
[6] Boufounos P T,Baraniuk R G. 1-bit compressive sensing[C]//Proceedings of 2008 42nd Annual Conference on Information Science and Systems. Princeton,NJ:IEEE,2008:16-21.
[7] Boufounos P T. Greedy sparse signal reconstruction from sign measurements[C]// Proceedings of the 43rd Asilomar Conference on Signals,Systems and Computers.Piscataway,NJ,USA:IEEE,2009:1305-1309.
[8] Laska J N,Wen Z,Yin W,et al. Trust,but verify:Fast and accurate signal recovery from 1-bit compressive measurement[J].IEEE Transactions on Signal Processing,2011,59(11):5289-5301.
[9] Jacques L,Laska J N,Boufounos P T,et al. Robust 1-bit compressive sensing via binary stable embeddings of sparse vectors[J].IEEE Transactions on Information Theory,2013,59(4):2082-2102.
[10] 杨海蓉,方红,张成,等. 基于回溯的迭代硬阀值算法[J]. 自动化学报,2011,37(3):276-282.YANG Hai-rong,FANG Hong,ZHANG Cheng,et al. Iterative Hard Thresholding Algorithm Based on Backtracking[J]. ACTA Automatica Sinica,2011,37(3),276-282.(in Chinese)
[11] 肖涛,马社祥. 一比特压缩传感的贪婪重构算法[J].科学技术与工程,2012,12(34):9182-9185.XIAO Tao,MA She-xiang. Greedy Reconstruction Algorithm of One-bit Compressed Sensing [J]. Science Technology and Engineering,2012,12(34):9182-9185.(in Chinese)

