基于中国剩余定理和贪婪算法扩展的QC－LDPC 码*

黄 胜，庞晓磊，田方方，贾雪婷

(重庆邮电大学 光纤通信技术重点实验室，重庆400065)

1 引 言

LDPC 码具有逼近Shannon 限的优秀性能［1］，而且译码复杂度较低，已经成为近几年编码学者的研究热点。目前LDPC 码的研究主要分为3 个方向，一是性能优化设计方法，二是降低编码复杂度［2］，三是在通信系统中的应用［3］，本文重点在性能优化设计方法方面。而LDPC 码的构造方法主要分为随机构造方法［4］和结构化构造方法［5］两类。由于随机码具有很大的编码复杂度，因此在实际应用中受到很大的限制。准循环(QC)LDPC 码是一个很好折衷方案，不仅具有非常优秀的性能，而且其代数结构大大降低了运算和存储复杂度，一些QCLDPC 码甚至具有和随机码比肩的优异性能［6］。

阵列码是一类具有特殊结构的QC－LDPC 码，不仅具有QC－LDPC 的代数结构，可以用简单的移位寄存器进行编码，同时也具有低错误平层、围长至少为6、纠突发错误的优点［7－8］。中国剩余定理(CRT)已被应用于计算机、编码、数字信号处理等领域，而结合CRT 的QC－LDPC 码已经被陆续研究［9－11］。利用CRT 构造LDPC 码的优势是，用若干个QC－LDPC 短码作为分量码可以构造出QC－LDPC 长码，并且QC－LDPC 长码的围长不小于所有分量码的最大围长。将阵列码作为分量码，文献［9］利用CRT 构造出了不含4 环的QC－LDPC 码，文献［10］利用CRT 方法构造出了一类不含4 环并且6环数量大大减少(但不能完全消除)的QC－LDPC码。由于阵列码的循环置换矩阵(CPM)尺寸为素数，因此这两种方法得到的QC－LDPC 码的码长取值非常受限。文献［11］构造的CRT 码虽然最短环数列较文献［12］构造的缩短阵列码(SAC)有一定的减少，但是还有进一步改进的空间。从目前CRT在LDPC 码的应用［9－11］可知，除了第一个是阵列码外，其他的分量码都是随机选择，导致新构造的码性能有不同程度的削弱。

基于以上问题，本文提出了一种结合CRT 和贪婪算法扩展QC－LDPC 码的构造方法，其循环置换子矩阵由0 矩阵、楼梯矩阵及其右移矩阵构成。该方法所构造的码与文献［9－11］不同，不仅码长更加灵活，而且围长更大，最重要的是只需已知一个分量码——缩短阵列码，通过CRT 和贪婪算法得出剩下分量码和最终所构造码。仿真结果表明本文提出的构造方法在AWGN 和瑞利衰落信道中与文献［11－12］的码字相比，当误码率为10－6时，净编码增益(NCG)有一定程度的改善，与Gallager 随机码性能相似但编码复杂度大大降低。

2 缩短阵列码的校验矩阵

QC－LDPC 码对应的校验矩阵由许多相同维数的子循环方阵组成，循环方阵由0 矩阵或者CPM组成。

QC－LDPC 码的校验矩阵可以表示为

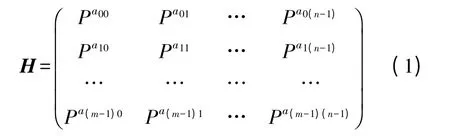
其中，aij∈﹛ 0，1，2，…，L－1，∞﹜。如果aij=∞，Paij(0≤i≤m－1，0≤j≤n－1)代表一个0 矩阵，否则表示一个循环右移单位矩阵aij次的L×L 循环置换矩阵。H 矩阵的m 块行记为从0 到m－1 块行，n 块列记为从0 到n－1 列。

校验矩阵H 的指数矩阵E(H)可以如式(2)表示:

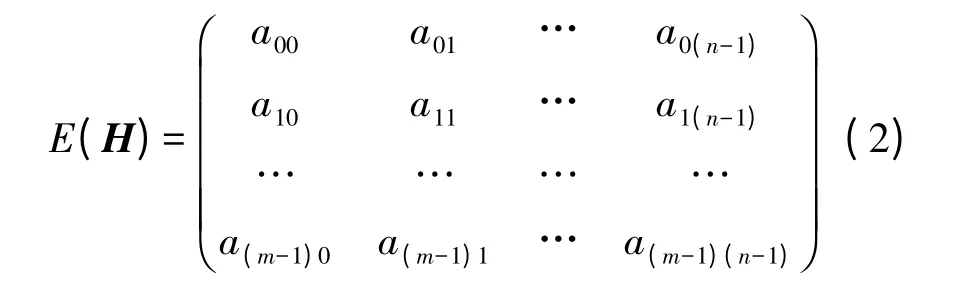
并且H 可以由E(H)中每个元素aij用Paij替代获得。

阵列码是一类基于L×L 循环置换矩阵的QCLDPC 码。阵列码的指数矩阵被定义为E(H)=(aij)，aij=i×j mod L，这里0≤i≤M－1 并且0≤j≤L－1，M 是正整数，L 是素数且保证M≤L。阵列码的校验矩阵［7］为

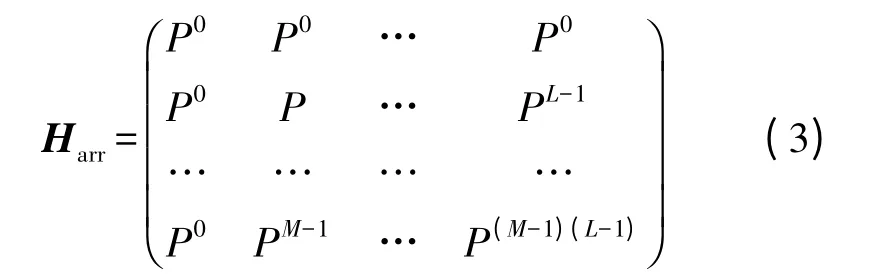
缩短阵列码为在阵列码的基础上删除特定的列的矩阵，以便获得更大围长［12］。

定理［7］:当在阵列码的校验矩阵H 中存在一个块行列指数对序列(i1，j1)，(i1，j2)，(i2，j2)，(i2，j3)，...，(ik，jk)，(ik，j1)使得i1(j1－j2)+i2(j2－j3)+...+ik(jk－j1)≡0 mod L，则此阵列码存在一个2k 环，其中il≠il+1，jl≠jl+1，l=1，2，…，k－1，且ik≠i1，jk≠j1。

图1是指数矩阵存在6 环的结构以及约束方程［12］。表1为对应列重为4 的指数矩阵存在环6的约束方程以及消除环的序列［12］。

图1 存在6 环的指数矩阵和对应的约束方程Fig.1 Exponent matrix with six cycles and its governing equation

表1 列重为4 的指数矩阵在模L 下对应的环6 约束方程和消去6 环的序列Table 1 Six cycle－governing equation for shortened array codes with modulus L and column－weight r=4，and greedy sequences avoiding solutions to six cycle－governing equation

3 基于CRT 和贪婪算法构造围长至少为8的QC－LDPC 码

由表1中消除所有环6 的序列可以得到缩短阵列码，但缩短阵列码获得的大围长是以牺牲特定的列获得的，因此缩短阵列码相对一般的阵列码具有较大围长且较短码长的特点。为进一步改善性能，把CRT 和贪婪算法结合起来扩展缩短阵列码以便获得更大围长、更加灵活的码长，如果围长一样，则使得最短环的数量尽可能地少。

设L1，L2，…，Ls是CRT 中s 个不同的的除数使得L=L1×L2…Ll…Lf…×Ls。其中f= 1，2，…，s，GCD(Ll，Lf)= 1(GCD 表示最大公约数)。设Cf是一个QC－LDPC 码，它的校验矩阵Hf是一个基于Lf×Lf的CPM 或者0 矩阵的m×n 阵列。而且E(Hf)=是Hl的一个指数矩阵。

在缩短阵列码的基础上结合CRT 和贪婪算法构造一个QC－LDPC 长码，它是一个mL×nL 的校验矩阵H。aij表示s 个分量码经过CRT 和贪婪算法之后形成新的码字H 的指数矩阵中的元素，步骤如下所示(符号说明:E(Hf)表示第f(f=1，2，…，s)个分量码指数矩阵，afij表示为E(Hf)的第i 行第j 列元素。E(Bf)表示第f 个临时新构造的指数矩阵，bfij为E(Bf)的第i 行第j 列元素):

(1)E(H1)置为上文所述缩短阵列码的指数矩阵，其余f－1 个分量码指数矩阵E(Hf)的第一行第一列的元素置为0;

(2)CRT:如果ri≠∞，其中i = 1，2，则t =这里且Ai为满足Ai≡1mod Ki约束条件的最小正整数;否则若ri=∞，则t=∞。其中，ri表示参与CRT 操作的指数矩阵中的元素，Ki表示参与CRT 运算对应指数矩阵循环置换矩阵的维数;

(3)利用CRT 和贪婪算法求E(Hf)和E(H)中的各个元素，如图2所示。

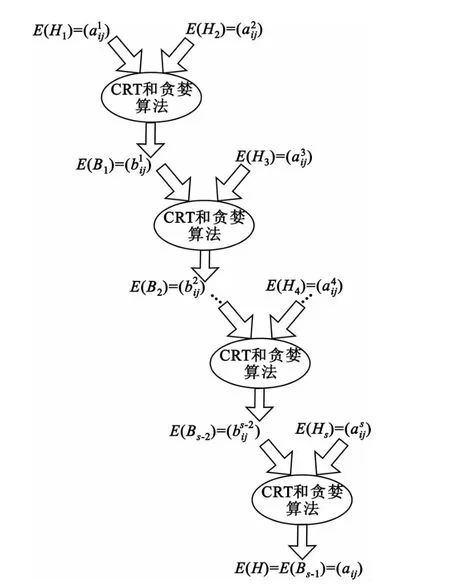
图2 获得aij与(2＜f≤s)的流程图Fig.2 Flow chart of acquring both aij and (2＜f≤s)

具体的步骤如下:

1)i=2，j=2;

2)根据E(H1)，利用CRT，计算E(B1)中的元素和E(H2)中的元素，确定的策略就是利用贪婪算法在0 至L2－1 中通过和E(H1)中对应位置的已知元素利用CRT 选择使当前构造的校验矩阵围长H1B最大的元素。如果有多个元素同时满足该条件，即选择同时使得当前分量码围长尽可能大的最小元素。在确定H1B中b1ij的同时也确定a2ij，维数变为

3)f 从2 到s 递增变化循环执行下面的操作:根据E(Bf)，利用CRT 计算E(Bf)中的元素bfij和E(Hf+1)中的元素确定的策略就是利用贪婪算法在0 至Lf+1－1 中通过和E(Bf)中对应位置的已知元素利用CRT 选择使当前构造的校验矩阵围长最大的元素。如果有多个元素同时满足该条件，即选择同时使得当前分量码围长尽可能大的最小元素，维数变为循环结束后，计算获得的E(Bs－1)中的元素bs－1ij，即为E(H)中的元素aij;

4)先递增i，再递增j，循环执行第2 步和第3步，计算出E(H)中的所有元素aij;

(4)将得到指数矩阵E(H)记为E(H)=(aij);

(5)把E(H)中的每个元素aij用Daij代替获得码字C 的校验矩阵H。其中循环置换D 矩阵不同于第2 节中的循环置换矩阵P，采用楼梯矩阵D，L阶楼梯矩阵D 的构造方法如下所示:

1)把第一个1 放在第一行第[L/2] 列;

2)接下来每一个数1 放在前一个数1 的右上一格;

3)如果这个数1 所要放的格已经超出了顶行那么就把它放在底行，仍然要放在右一列;

4)如果这个数1 所要放的格已经超出了最右列那么就把它放在最左列，仍然要放在上一行;

5)按照上面的方法放置L 次后保证所得L 阶矩阵每行每列只有一个数1。

引理［9］:假设l=1，2，…，s，让gl记为分量码Cl的围长，g 为s 个分量码经过CRT 构造的码C 的围长，则g≥max{g1，g2，…，gs}。

推论:如果存在任意s 个两两互素的数L1，L2，…，Ls，则其中任意l 个数的乘积与剩下的s－l 个数两两互素，其中1＜l≤s。

证明:由s 个两两互素的数可知GCD(Lα，Lβ)=1，其中1≤α，β≤s 且α≠β。A= L1×L2…Ll，B=Lf，l＜f≤s，GCD(A，B)≠1，则存在GCD(Lγ，Lf)≠1，1≤γ≤l。这显然与题目条件矛盾，所以假设不成立，原命题成立。

由上述定理和推论可知，经过CRT 和贪婪算法，由上述方法构造的新码围长依次为gB1≥max{g1，g2}→gB2≥max{gB1，g3}→…→gBs－2≥max{gBs－3，gs－1}→g≥max{gBs－2，gs}gBi(1≤i≤s－2)。

通过上述分析，本文通过CRT 和贪婪算法构造的新码与传统的CRT 方法扩展的LDPC 码［9－11］不同，不仅具有灵活的码长和更大的围长，如果围长一样，则最短环的数量尽可能地少，而且只需要一个分量码即可。

4 仿真与性能分析

4.1 LDPC 码在加性高斯白噪声信道下的性能仿真

本文仿真中调制方法采用的是BPSK 调制，传输信道选用的是加性高斯白噪声(AWGN)信道，采用BP 译码算法。首先仿真了所构造的码字在BP译码算法中不同迭代次数时的纠错性能，如图3所示。由图3可知QC－LDPC(7592，3796)码随着迭代次数的增大，其NCG 有一定的提高，但是迭代次数到达一定次数时，其NCG 的差别就越来越小，甚至不再提高，但是迭代次数的增加会增加译码的复杂度，译码耗时就越长。综合以上分析本文折衷选择迭代次数16。

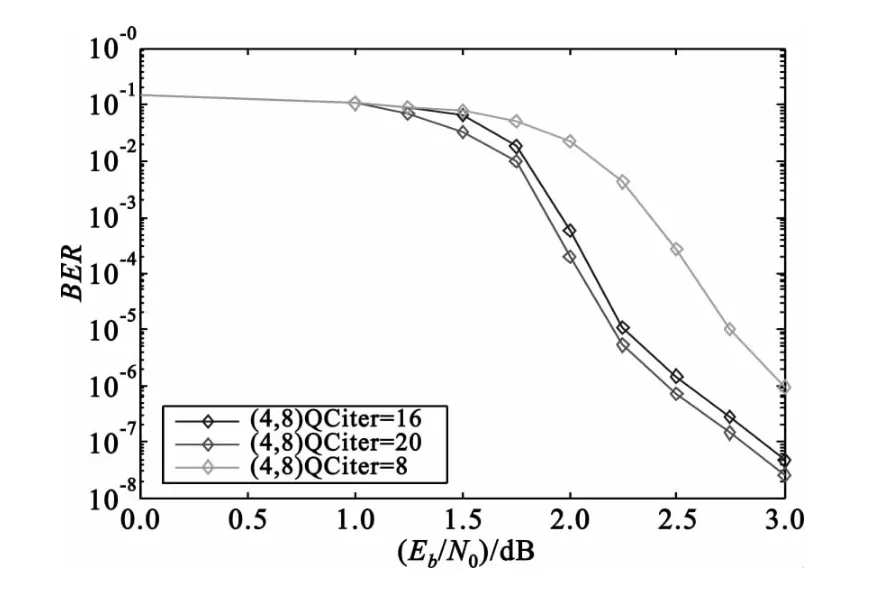
图3 不同迭代次数时QC－LDPC(7592，3796)码纠错性能Fig.3 Error correction performance of QC－LDPC code(7592，3796)with different number of iterations

利用表1构造一个围长为8、列重为4 的缩短阵列码，其校验矩阵H1是一个基于73×73 的循环置换子矩阵的4×8 阵列。为把H1扩展为一个949×949 的循环置换子矩阵的4×8 阵列。首先，选择s=2，L2=13，则L=949。利用贪婪算法构造一个维数是4×8 阵列码指数矩阵E(H2)，其次通过CRT 和贪婪算法构造E(H)。最后把E(H)中的每个元素aij用Daij代替，获得了一个围长为8 的QC－LDPC 码字C，但是新构造的码最短环的数量相对于文献［11－12］大大降低，具体如表2所示。图4为构造码字的误比特率性能曲线。为了充分说明本文提出码字的纠错性能，文献［12］中的缩短阵列码(SAC)和文献［11］中的CRT 码以及Gallager 随机码也在图中显示。从图3中可以看出在相同码长、码率、列重的条件下，本文提出的QC－LDPC 码字在10－6误码率条件下比文献［12］中的码字有1.2 dB 左右的NCG，比文献［11］的码字有0.3 dB左右的改善，和Gallagher 随机码具有相似性能但编码复杂度大大降低。

表2 不同算法构造的QC－LDPC 码对应的最短环的数量Table 2 The number of the shortest cycles through constructing QC－LDPC codes via different algorithms

图4 不同算法构造的码率为1/2 且相同码长、列重为4条件下的QC－LDPC 码在AWGN 信道下误码率性能对比Fig.4 BER performance of constructing QC－LDPC codes by different algorithms with the same code rate，code length and column－weight r=4 in AWGN channel

4.2 LDPC 码在瑞利衰落信道下的性能仿真

LDPC 码在瑞利衰落信道的性能仿真对比如图5所示，采用BPSK 调制，BP 译码算法，瑞利衰落信道Ts=0.5×10－6，fd=100，未知初始信道状态信息，迭代30 次。

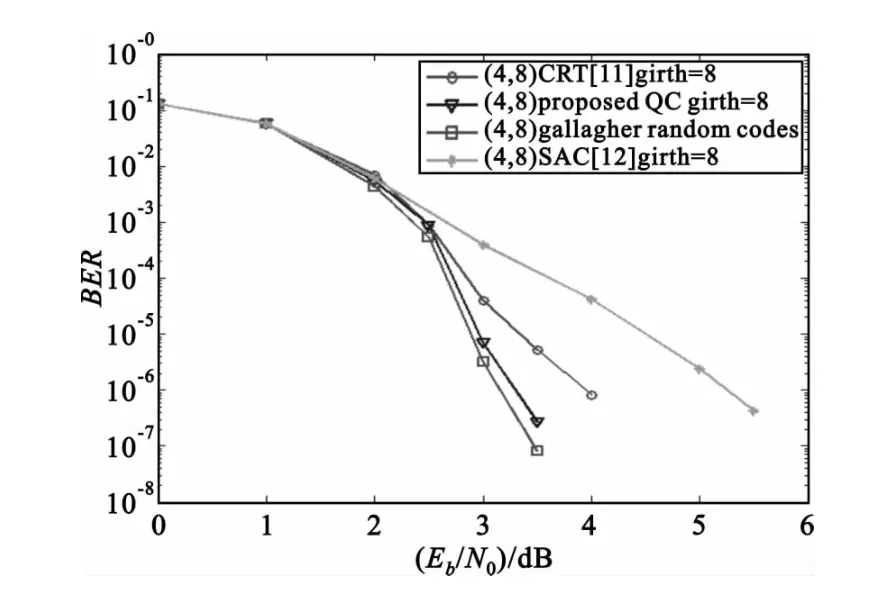
图5 不同算法构造的码率为1/2 且相同码长、列重为4条件下的QC－LDPC 码在瑞利衰落信道下误码率性能对比Fig.4 BER performance of constructing QC－LDPC codes by different algorithms with the same code rate，code length and column－weight r=4 in Rayleigh fading channel

从图5中可以看出在相同码长、码率、列重的条件下，本文提出的QC－LDPC 码字在10－6误码率条件下比文献［12］中的码字有2 dB左右的NCG，比文献［11］的码字有0.7 dB左右的改善，和Gallagher 随机码具有相似性能但编码复杂度大大降低。

通过上述仿真可知，无论瑞利衰落信道还是AWGN 信道，本文提出算法相比其他算法均具有更好的性能，通过不同信道下的NCG 对比，本文提出的算法更具抗干扰性。

5 结 论

本文利用CRT 和贪婪算法，在缩短阵列码基础上通过CRT 和贪婪算法构造更大围长和码长更加灵活的QC－LDPC 码字，所构造的码字的校验矩阵是采用楼梯矩阵D 循环置换而成。与目前CRT 在LDPC码的应用相比，本文所提出的码字的构造只需已知一个分量码——缩短阵列码，通过CRT 和贪婪算法得出剩下分量码和最终所构造码，同时码尽可能大地增大围长，如果围长一样，则尽可能地降低最短环的数量。仿真结果表明，在AWGN 信道和瑞利衰落信道条件下，本文提出的构造方法性能均优于文献［11－12］中构造的码字，具有更好的抗干扰性能，且与Gallager 随机码在相同条件下具有相似的性能但具有较低的编码复杂度，由此可见，本文提出的构造方案在不同的信道环境下均有较强的竞争力，为未来移动通信系统纠错码提供了一种选择方案。

在今后的研究工作中，可以在本文提出的构造方法基础上，与双对角线结构相结合并进行一定的改进，以便在降低编码复杂度的同时尽可能地减少对性能的削弱。

［1］ MacKay D J C，Neal R M.Near Shannon limit performance of low density parity check codes［J］.Electronics Letters，1996，32(18):1645.

［2］ 刘原华，张美玲.一种可快速编码的QC—LDPC 码构造新方法［J］.电讯技术，2013，53(1):55－59.LIU Yuan－hua，ZHANG Mei－ling.A New Desin Method for Quasi－cycle LDPC Codes with Fast Encoding Ability［J］.Telecommunication Engineering，2013，53(1):55－59.(in Chinese)

［3］ 程浩，仰枫帆.基于有限域的QC－LDPC 码编码协作通信及其联合迭代译码技术［J］.电讯技术，2013，53(12):1574－1579.CHENG Hao，YANG Feng－fan.Finite Field QC－LDPCbased Encoding Cooperative System and its Joint Iterative Decoding Technology［J］.Telecommunication Engineering，2013，53(12):1574－1579.(in Chinese)

［4］ Khazraie S，Asvadi R，Banihashemi A H.A PEG construction of finite－Length LDPC codes with low error floor［J］.IEEE Communications Letters，2012，16(8):1288－1291.

［5］ Wang L，Zhang X，Yu F，et al.QC－LDPC Codes with Girth Eight Based on Independent Row－Column Mapping Sequence［J］.IEEE Communications Letters，2013，17(11):2140－2143.

［6］ Fossorier M P C.Quasi－cyclic low－density parity－check codes from circulant permutation matrices［J］.IEEE Transactions on Information Theory，2004，50(8):1788－1793.

［7］ Fan J L.Array codes as LDPC codes［M］//Constrained Coding and Soft Iterative Decoding. Berlin:Springer，2001:195－203.

［8］ Blaum M，Roth R M.New array codes for multiple phased burst correction［J］.IEEE Transactions on Information Theory，1993，39(1):66－77.

［9］ Myung S，Yang K.A combining method of quasi－cyclic LDPC codes by the Chinese remainder theorem［J］.IEEE Communications Letters，2005，9(9):823－825.

［10］ Liu Y，Wang X，Chen R，et al.Generalized combining method for design of quasi－cyclic LDPC codes［J］.IEEE Communications Letters，2008，12(5):392－394.

［11］ Jiang X，Lee M H.Large girth quasi－cyclic LDPC codes based on the chinese remainder theorem［J］.IEEE Communications Letters，2009，13(5):342－344.

［12］ Milenkovic O，Kashyap N，Leyba D. Shortened array codes of large girth［J］.IEEE Transactions on Information Theory，2006，52(8):3707－3722.