粗糙集在教学评价系统中的应用

王琳燕

(福州职业技术学院计算机系，福建福州350003)

1 问题的提出

每个学期末，各校通常都要组织学生对每位任课教师的教学效果做出评价。我校使用的教学评价系统的样例数据如表1所示。该评价结果既能作为教师考核的依据，也能作为教师进行教学改革的重要参考。

作为一名教师，如果明确表中哪些关键因素决定教学评价结果，进行教学改革就会有的放矢，达到更好的教学效果。表1中评价项目较多，如何从中找出决定教学评价效果的关键因素呢?本文利用粗糙集理论中的属性约简技术较为简单地解决了这个特征选取问题。

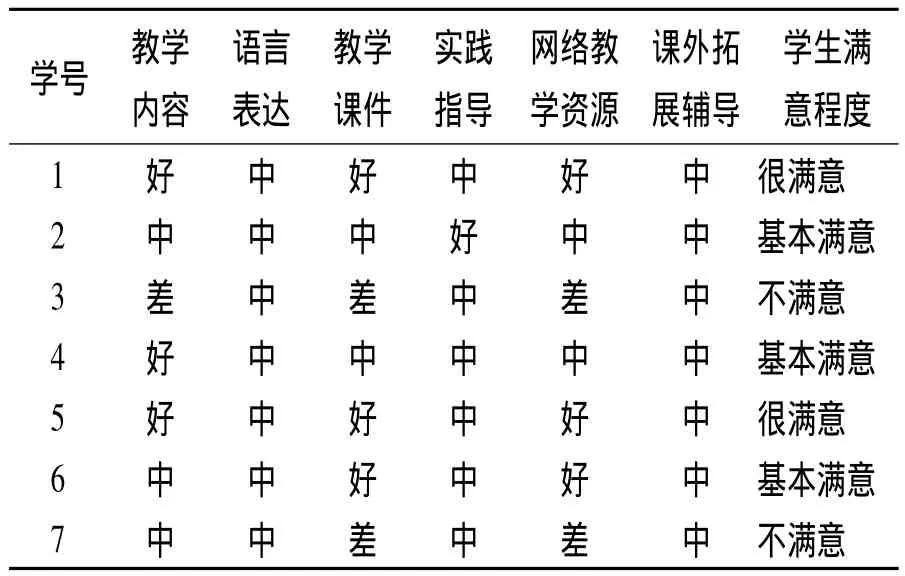
表1 教学评价系统的样例数据

2 粗糙集中基于差别矩阵的属性约简方法

粗糙集理论于1982年由Pawlak Z提出［1］，它是一种处理模糊和不确定性知识的数学工具［2］。属性约简是粗糙集理论中的一个重要研究课题。所谓属性约简，就是在保持知识库分类或决策能力不变的条件下删除其中不相关或不重要的知识，求得知识的最小表达和知识的各种不同颗粒层次［3］。为了后续叙述方便，下面给出几个相关概念。

定义1 考虑一个信息系统L=(U，Q，Vq，Fq)，q∈Q，其中U={x1，x2，…，xn}是论域，Q是属性集合，Vq为属性取值，Fq是U×Q→Vq的映射。属性集合 Q通常分为条件属性C={C1，C2，…，Cr}和决策属性集D。每一个属性子集P∈Q决定了一个二元不可区分关系IND(P):IND(P)={(x，y)∈U×U |a∈P，Fq(x，a)=Fq(y，a)}。关系IND(P)构成了U的一个划分，用U/IND(P)表示。

定义2 令R为一族等价关系，P∈R，如果IND(R)=IND(R－{P})，则称P为R中不必要的，否则称P为R中必要的。如果每一个P∈R都为R中必要的，则称R为独立的。

定义3 设U是一个论域，R、P为定义在 U上的2个等价关系簇，且R⊆P，如果满足:①IND(P)=IND(R);②R是独立的，称R是P的一个约简。

定义4 所有属性约简的交集成为核。

Hu等人根据 Skowron差别矩阵［4］提出一种基于属性重要性的启发式属性约简算法［5］。其基本思想是将信息系统中所有相关属性的区分信息都浓缩进一个矩阵中，通过差别矩阵可以方便地得到信息系统中的属性核。Hu在文献［6］中提出利用改进的差别矩阵求核，其中改进的差别矩阵的定义如式(1):

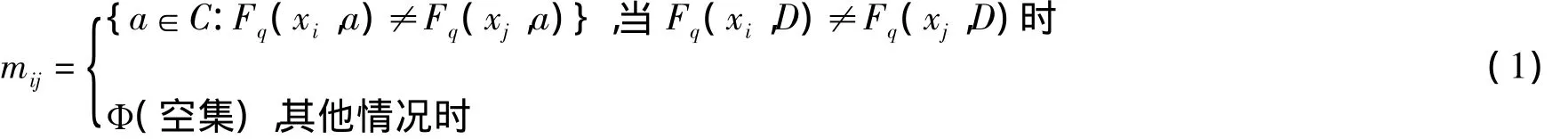
Hu认为当且仅当 某个 mij为单个属性时，该属性属于核。有学者在文献［7］中指出了Hu中差别矩阵的求核缺陷，提出新的差别矩阵定义并加以证明。具体差别矩阵的定义M={m'ij}如式(2):

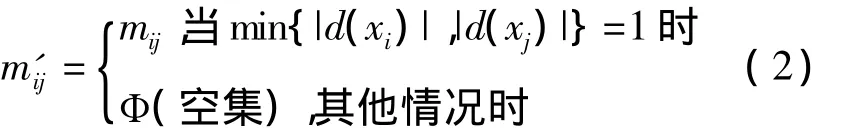
其中d(xi)表示 U中所有与 xi在关系IND(C)下是等价的元素相应的决策属性值构成的集合的基数。

差别矩阵在求属性约简过程中最大缺点为对空间要求过大，文献［8］中提出的部分差别矩阵可以减少差别矩阵存储上的空间复杂度，但在处理属性重要度方面有一定的缺陷，本文采用的属性约简算法在文献［8］的基础上做了一点改进。

3 教学评价系统的特征选取过程

3.1 特征选取设计总体方案

本文采用的特征选取方案如图1所示。该方案的流程是:首先将教学评价系统中与评价结果有关的数据用二维表的方式提取出来，去除重复数据后对数据表进行离散化处理，然后运用一种属性约简算法进行特征选取，最后得到一个属性约简子集，也就是教学评价系统中决定教学评价效果的关键因素。

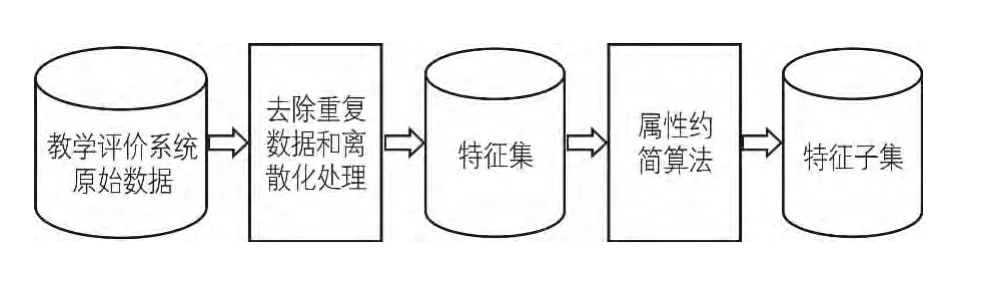
图1 设计方案

3.2 去除重复数据和离散化处理

为了方便数据的处理，用C1，C2，C3，……分别表示教学内容、语言表达、教学课件等评价项目，用D表示评价结果。对表1中的数据进行数值化处理。各项评价指标中分别用1、2、3表示好、中、差。评价结果中用1、2、3分别表示满意、基本满意、不满意，并将表1中的第5条重复数据去除，经过以上处理，表1中的数据就被整理成表2的数据。

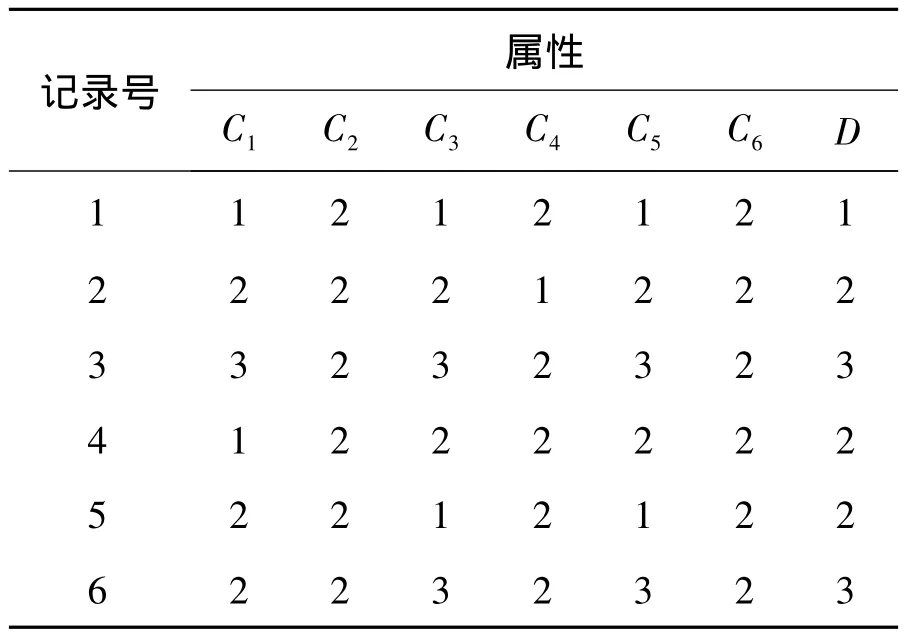
表2 处理后的样例数据

需要说明的是如果有的学校教学评价项目采用打分的方式，则在这一步要做离散化处理。比如90-100分用1表示，80-90分用2表示等，同样也可以处理成类似于表2的数据。

3.3 改进的基于差别矩阵的属性约简算法的实现

本文采用的属性约简算法的流程如图2所示。

图2 属性约简算法流程图

1)差别矩阵的定义及求核。本文采用文献［7］的差别矩阵求核。根据式(1)和(2)的定义，表2数据对应的差别矩阵如表3所示。在表3中根据公式(1)求得核为C1。

表3 教学评价数据的差别矩阵

2)简化差别矩阵。设属性约简集合R= {核}，将差别矩阵中包含核C1的元素置为空集。这个步骤与文献［8］中提出的部分差别矩阵的思路是一致的。简化后的差别矩阵如表4所示。

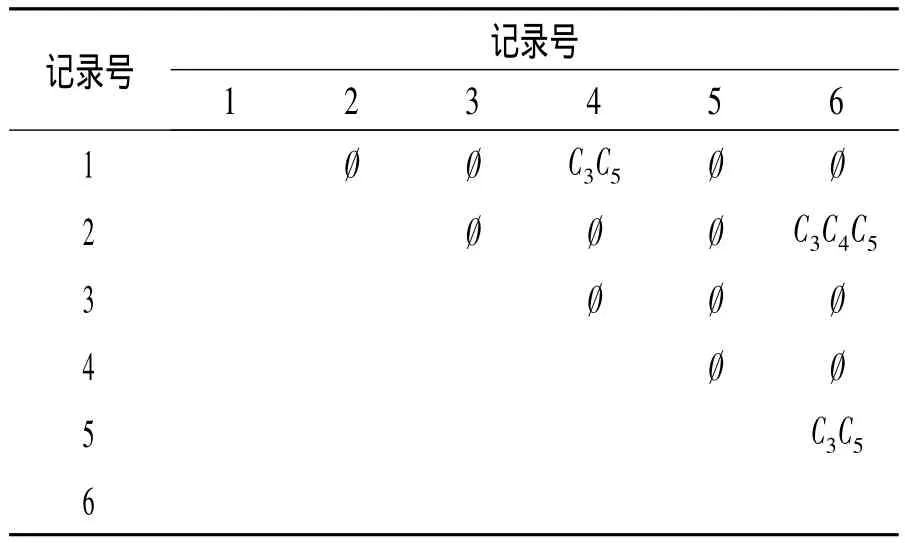
表4 简化后的差别矩阵

3)按照属性的重要性依次将属性添加到约简集R中，然后继续简化差别矩阵直到差别矩阵全部元素都为空则算法停止。

用属性在差别矩阵中出现的频率f作为属性重要性的衡量标准，找出f最高的那个属性。文献［8］中对f取值相同的属性随机选取一个，但这样的选择具有一定的盲目性。在差别矩阵中，如果某个矩阵元素包含的属性个数越少，则这个矩阵元素一定更为精辟且更为重要。因此，将包含该属性的所有矩阵元素的长度的累加和s作为辅助属性重要性的衡量标准，对于f相同的属性，根据f/s得到商g。根据g值从大到小的顺序将这些f相同的属性放入一个队列。

4)从队列中取出一个属性a加入R。

5)由于属性a已经加入属性约简集，可以继续简化差别矩阵，将矩阵中包含a的元素全部置为空。

6)若矩阵全部元素都为空，则算法停止。

7)查看队列中是否还有元素，如果有则转入步骤4，否则进入步骤3。

3.4 实验结果和分析

为了验证算法，将计算机系2012年教学评价数据作为测试数据，运用以上算法最后求得属性约简为 C1，C3。也就是说通过属性约简算法，可以在众多的评价因子中找出教学内容和教学课件是决定教学效果的重要因素，减少了今后做进一步数据挖掘的数据运算量。该算法的时间复杂度为:O(|C|2|U|2)。

3.5 对空间复杂度的改进

差别矩阵对空间要求很大，本文采用的算法在步骤2上对差别矩阵进行简化，另外由于差别矩阵是对称矩阵，在存储时只需存储上半矩阵，这样能使空间复杂度减少一半。

4 结论

本文利用差别矩阵的特性，采用改进的属性约简算法，得到教学评价系统中决定教学效果的关键因素，并解决了空间复杂度的问题。本文中提到的算法也可以比较简单地解决其他类似的属性约简的实际问题。

［1］ Pawlak Z.Rough sets［J］.International Journal of Information and Computer Sciences，1982，11(5): 341－356.

［2］ 张文修，吴伟志，梁吉业，等.粗糙集理论与方法［M］.北京:科学出版社，2001:11.

［3］ 王柯，朱启兵.一种基于差别矩阵的启发式属性约简算法［J］.计算机工程与科学，2008，30 (6):73－75.

［4］ 蒙韧，徐章艳，杨炳儒.一个计算Skowron差别矩阵核的新算法［J］.计算机工程与应用，2011，47(1):159－161.

［5］ 杨传健，葛浩，汪志圣.基于粗糙集的属性约简方法研究综述［J］.计算机应用研究，2012，29 (1):16－20.

［6］ Hu Xiaohua，N Cercone.Learning in relational databases:a rough set approach［J］.Computational Intelligence，1995，11(2):323－337.

［7］ 叶东毅，陈昭炯.一个新的差别矩阵及其求核方法［J］.电子学报，2002，30(7):1086－1088.

［8］ 徐一新，叶东毅.知识约简的差别矩阵启发式算法［J］.福州大学学报(自然科学版)，2000，28 (3):121－123.