一个无证书的代理重加密方案设计

刘志远，邱 阳

(湖北理工学院计算机学院，湖北黄石435003)

随着计算机网络技术的飞速发展和社会的不断进步，计算机用户对自己存储在分布式网络环境中的数据安全性和共享性的关注越来越多。如加密邮件的转发、跨域数据的访问以及分布式文件系统存储等应用的安全性问题得到了广泛的关注。如何保障用户在这些应用中的数据安全性和共享性是一个亟待解决的问题。代理重加密［1］(Proxy Re－encryption，PRE)方案是一个比较有用的密码学工具，它也是解决上述问题的有效方法之一。

代理重加密方案的工作流程通常包含有4个角色和3个功能。4个角色可以分别描述为:密钥生成中心 (Key Generator Center，KGC)、数据拥有者(授传人)、数据共享者(受理人)和一个半可信的代理人(即相信其肯定会将数据拥有者的密文按照给出的方法转换成数据共享者的密文)。3个功能分别是密码系统参数生成、数据拥有者的数据加密存储和数据共享者的密文数据共享转换。代理重加密最早由文献［1］提出，随后得到了广泛的研究。按照密文转换的方向可以将其分为2类:单向代理重加密和双向代理重加密。单向代理重加密是指代理人只能将授权者的密文转换为共享者的密文，反之则不行，常见的单向代理重加密方案可参考文献［2－4］;双向代理重加密则是指代理人既可以将授权者的密文转换为共享者的密文，也可以将共享者的密文转换为授权者的密文，常见的双向代理重加密方案可参考文献［1，5］。构造一个安全的单向代理重加密方案往往比构造一个双向代理重加密方案难得多，这是由于任何单向代理重加密方案都可以很容易地变成双向代理重加密方案，而由双向代理重加密方案到单向代理重加密方案的变换目前尚未知道是否存在［3］。另外，根据密文可转换次数的不同，可以将重加密方案分为单跳代理重加密方案和多跳代理重加密方案［4，6］。在构造代理重加密方案时，必须防止代理人与授权人合谋获取共享者的私钥或代理人与共享者合谋获取授权人的私钥，文献［1，5］的代理重加密方案就存在这样的合谋攻击，并且在文献［5］中提出了这样一个公开的问题:如何构造选择密文安全的代理重加密方案。2009年，基于文献［5］提出的问题，Shao等人［7］利用双线性对构造了一个选择密文安全的代理重加密方案，并且该方案的效率较高。但不幸的是，文献［3］指出该方案连选择明文安全也无法满足。因此尽管代理重加密有很好的应用前景，但是仍有许多问题尚待解决，比如基于身份的代理重加密方案存在的密钥托管问题。

本文先给出构造代理重加密方案所需的相关数学知识，然后在文献［8］的基础上，提出一个无证书的代理重加密方案，并给出了方案的安全性证明。

1 预备知识

1.1 双线性映射

设G1是由P生成的循环群，阶为素数q。G2是一个乘法循环群，阶也为q。双线性映射:G1×G1→G2的性质如下:

3)可计算性:∀u，v∈G1，由一个多项式时间算法来计算(u，v)。

双线性映射最早由文献［9］提出，并用于求解椭圆曲线群的离散对数问题。因其特有的双线性性质，2000年以后被广泛应用于各类密码方案的设计中。

1.2 困难性假设

设G1是由 g生成的加法循环群，阶为素数q。G2是一个乘法循环群，阶也为q。双线性映射为:G1×G1→G2。

1)Bilinear Diffie－Hellman问题是:∀a，b，c∈，给定P，aP，bP，cP，计算(P，P)abc。

2)Decisional Bilinear Diffie－Hellman问题是:∀a，b，c∈，给定 P，aP，bP，cP和h∈G2，判断h=(P，P)abc是否成立。

2 无证书代理重加密方案

基于文献［8］构造了一个无证书的代理重加密方案，方案的构造过程和文献［10］相类似。该方案由以下算法组成:

1)Setup(1k)算法:该算法由KGC执行，通过输入安全参数1k，生成系统用的主公开参数和主秘密参数，具体过程如下:

①生成2个大素数，即p阶群G、GT、G的生成元P和双线性映射:G×G→GT;

③生成主公开参数PK=(G，GT，g，Pub= sP，，H1，H2)和主秘密参数MK=s。

2)Extract(MK，ID)算法:该算法由KGC执行，通过输入主秘密参数MK和身份信息ID，为身份信息ID生成对应的私钥，具体过程如下:

①身份信息ID对应的部分私钥为D=sH1(ID);

②KGC通过安全信道将D=sH1(ID)传递给用户ID;

④身份信息为ID的用户的公钥为PKID=＜X，Y＞=＜xP，xsP＞。

3)Enc(PK，ID，SKID，t，m)算法:该算法通过输入主公开参数PK、身份信息 ID、身份信息ID对应的私钥SKID，明文m∈G，由明文m的拥有者采用自己的身份信息ID生成密文c=(c1，c2)，其中c1，c2和c3的计算分别如下:

②c2=m·(H1(ID)，YA)r·H2(SKID)。

4)Dec(c，SKID)算法:该算法通过输入密文c=(c1，c2)和私钥SKID，由私钥的拥有者对密文c进行解密，具体的解密算法如下:

5)RKey(IDA，IDB，SKIDA)算法:该算法由数据拥有者IDA执行，通过输入数据拥有者的身份信息IDA、私钥SKIDA和共享者的身份信息IDB，为预共享者 IDB生成代理重加密密钥RKIDA→IDB，具体的执行过程如下:

②计算 RKIDA→IDB=(· H1 (R)，r'P，R·(H1(IDB)，YA)r')。

6)REnc(c，RKIDA→IDB)算法:该算法由代理人执行，通过输入预共享密文c=(c1，c2)和代理重加密密钥 RKIDA→IDB，实现预共享密文 c的所有权从其拥有者IDA到共享者IDB的转换，并生成可由共享者IDB解密的密文c'=(c'1，c'2，c'3，c'4)，具体的执行过程如下:

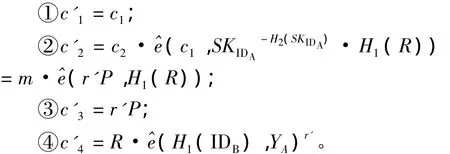
7)RDec(c'，SKIDB)算法:该算法由共享者IDB执行，通过输入共享者 IDB的密文 c'= (c'1，c'2，c'3，c'4)和共享者 IDB的私钥 SKIDB，解密出共享的明文m，具体的执行过程如下:

3 安全性分析

基于身份的密码体制通常存在密钥托管问题，但本文的代理重加密方案是基于无证书密码体制实现的，因而避免了密钥托管问题，即使有恶意的KGC存在，该方案也是安全的。但是基于无证书的密码方案天然存在着2类攻击:①可以替换用户的公钥就不能拥有系统的主密钥;②拥有系统的主密钥就不能替换用户的公钥。本文提出的方案是基于文献［8］实现的，对于抵御以上2类攻击的过程已在文献［8］中得到证明，因此基于无证书的代理重加密方案是能够抵御这2类攻击的，具体证明过程见文献［8］。本文主要从以下几个方面来分析该方案的安全性:①单向性;②合谋攻击;③密钥替换攻击;④非传递性。

1)单向性。由文中方案的 RKey(IDA，IDB，SKIDA)算法可知:重加密密钥为 RKIDA→IDB·H1(R)，r'P，R·(H1(IDB)，Y)r')，从RKIDA→IDB中可以看到，重加密密钥中包含有用户A的私钥 SKIDA，要想获得用户A的私钥 SKIDA，则必须解决 DL困难问题，而该困难问题是无法解决的，因此可知从RKIDA→IDB中得到 RKIDB→IDA是困难的，所以文中的方案满足单向性。

2)合谋攻击。合谋攻击可以从以下2个方面来分析。①代理人和数据共享者合谋获取授权人的私钥。通过上述对代理重加密算法的分析可知，授权人的私钥在c2和 RKIDA→IDB中出现过，想获取授权人的私钥必须计算或 H2(SKIDA)来得到 SKIDA，这等同于解决DL困难问题。②代理人和授权人合谋获取数据共享者的私钥。同样观察上述代理重加密算法可知，数据共享者的私钥在RDec(c'，SKIDB)中出现过，要想获得数据共享者的私钥SKIDB，则必须解决DL困难问题。综上可知，该方案是可以抵抗合谋攻击的。

3)密钥替换攻击。从上述代理重加密算法中可知，敌手展开密钥替换攻击只可能替换， 而 不 能 得 到 R， 故 在计算中得到的不是真正的明文m。因此敌手密钥替换攻击不成功。

4)非传递性。传递性是指存在用户A、用户B和用户 C，由 RKIDA→IDB和 RKIDB→IDC可以计算得到 RK。由 RK=(SK－H2(SKIDi)IDA→IDCIDi→IDjIDi·H1(R)，r'P，R·(H1(IDj)，Yi)r')可知，r'、R是任意选取的。RKIDA→IDC由3个部分组成，由RKIDA→IDB和RKIDB→IDC计算r'P是等同于求解DL难题。故文中的无证书代理重加密方案不具有传递性。

4 结论

基于文献［8］提出了一个无证书代理重加密方案。通过对方案的安全性进行分析，证明该方案不仅具有无证书密码方案的优点，还具有代理重加密方案的安全性。下一步的研究重点是如何在标准模型下构造一个单向的不用双线性对的代理重加密方案。

［1］ Matt Blaze，Gerrit Bleumer，Martin Strauss.Divertible Protocols and Atomic Proxy Cryptography［C］.Advances in Cryptology－EUROCRYPT＇98，1998:127－144.

［3］ 翁健，陈泯融，杨艳江，等.无需随机预言机的自适应攻陷模型下选择密文安全的单向代理重加密方案［J］.中国科学:信息科学，2010，40(2):298－312.

［4］ Wang H B，Cao Z F，Wang L C.Multi－use and unidirectional identity－based proxy re－encryption schemes［J］.Information Sciences，2010，180(20):4042－4059.

［5］ Canetti R，Hohenberger S.Chosen－ciphertext secure proxy re－encryption［C］.ACM Conference on Computer and Communication Security，2007:185－194.

［6］ Shao J，Liu P，Cao Z F.Multi－use Unidirectional Proxy Re－Encryption［C］.IEEE International Conference on Communications(ICC)，2011:1－5.

［7］ Shao J，Cao Z.CCA－secure Proxy re－encryption without pairings［C］.Public Key Cryptography，LNCS，2009:357－376.

［8］ Al－Riyami S S，Paterson K G.Certificateless-Public Key Crytography［J/OL］.(2003－07－02)［2013－08－14］.http//eprint.iacr.org/ 2003/126.pdf.

［9］ Alfred JM，Okamoto T，Scott A.Vanstone.Reducing Elliptic Curve Logarithms to Logarithms in a Finite Field［J］.IEEE Transactions on Information Theory，1993，39(5):1639－1646.

［10］ Ibraimi L，Tang Q，Hartel P.A Type－and－I-dentity－based Proxy Re－Encryption Scheme and its Application in Healthcare［C］.Secure Data Management，Springer LNCS 5159，2008: 185－198.