非一致激励多跨连续梁桥地震反应分析

王金海

（中铁六局集团天津铁路建设有限公司，天津300232）

0 引 言

我国地处世界两大地震带之间，是地球上地震最活跃的地区之一.尤其近年来我国多地相继发生了地震，桥梁结构的地震反应分析也成为研究的热点问题.据统计，我国境内的地震约占世界大陆地震的三分之一［1］.因此，桥梁抗震分析一直是桥梁研究中十分重要问题.地震动以波的形式传播，到达桥梁各支承点的时间不同，输入地震波时需要考虑桥墩之间的相位差而采用非一致性输入.目前非一致性输入最常用的方法是行波法.张静娟等以某座12跨预应力混凝土连续梁桥为例采用有限元结构分析软件ANSYS，通过输入不同波速的地震波，发现随着波速的增大，桥梁的地震反应先减小后增大［2］.王明晔等利用SAP2000分析行波效应对于多跨连续梁桥影响的规律性和影响行波效应的因素［3］.本文以某座13跨预应力连续梁桥为例，利于有限元软件MIDAS采用确定性时程分析方法［4］，对墩底剪力、墩顶位移等要素进行分析，将非一致激励结果与一致激励结果进行对比分析.

1 非一致地震动分析

非一致地震动输入的确定性方法主要是通过在不同支承点输入不同的地震波或以某条波为基准在不同点进行相位调整来考虑地震动的空间变化特性.非一致激励地震动输入最早采用的是行波法，行波法假定波的振幅会随传播的时间而逐渐衰减，但是波形会保持不变并按一定的速度沿地面传播.假设地震动在传播方向的一点a的地震动加速度üa（t），那么地震动传播到下一点b的地震动加速度为：

其中，v是地震动的传播速度，d是a点与b点的距离，C是振幅的衰减系数，由于地震动在较小的长度范围内的衰减不明显，因此取C＝1.可以根据加速度积分得出b点的速度和位移.

2 工程实例

2.1 工程概况

天津－保定铁路客运专线上的某特大桥，全长11570m，其中一段道岔梁采用预应力混凝土连续梁桥，跨径布置为（30.226＋11×31.176＋30.226）m.梁体采用单箱四室预应力混凝土箱梁结构，梁体高3m，第5跨到第7跨为道岔段，由单箱四室逐渐变为单箱六室，第11跨到第13跨的桥面采用变截面设计，桥面宽度由22.3m变为27.65m.主梁采用C55混凝土，普通钢筋采用HRB335钢筋和HPB300钢筋，预应力钢束采用直径15.2mm，抗拉强度标准值为1860MPa的高强低松弛钢绞线.全桥张拉的腹板预应力钢筋和支座负筋共520根，张拉强度为1395MPa.桥墩高度在12m至16m范围内变化，桥墩采用变截面设计，宽度从2.5m开始，按1：45的斜率逐渐变宽，桥墩竖向钢筋采用φ16HRB 335钢筋，箍筋采用φ12HRB 335钢筋.支座采用球型钢支座，型号分别为LXQZ－4000、5000、6500、7500、8000、10000、12500、15000、17500，道岔段支座由5个逐渐变为7个，而其他桥墩都使5个支座，每个桥墩的支座根据设计采用相应型号的球型刚支座.建立有限元模型如下图1.

图1 建立的midas有限元模型

2.2 桩土模拟

桩土共同作用用等代土模拟，等代土弹簧的刚度采用表征土介质弹性值的m参数来计算，等代土弹簧采用节点弹性支撑进行模拟.

2.3 地震动输入

《铁路工程抗震设计规范》中规定验算桥梁抗震时，需要分别计算横桥向和顺桥向的水平地震作用，最不利组合为：Ex＋0.65Ey和Ey＋0.65Ey.Ex和Ey分别为顺桥向和横桥向水平地震作用.由于桥址所在地区的地震烈度为7度震区（地震动加速度≤0.15g），选取具有代表意义的EI centro地震波，并对波形进行折减，折减系数为0.42，折减后的加速度峰值为0.15g.图2为EI centro地震波的时程曲线.

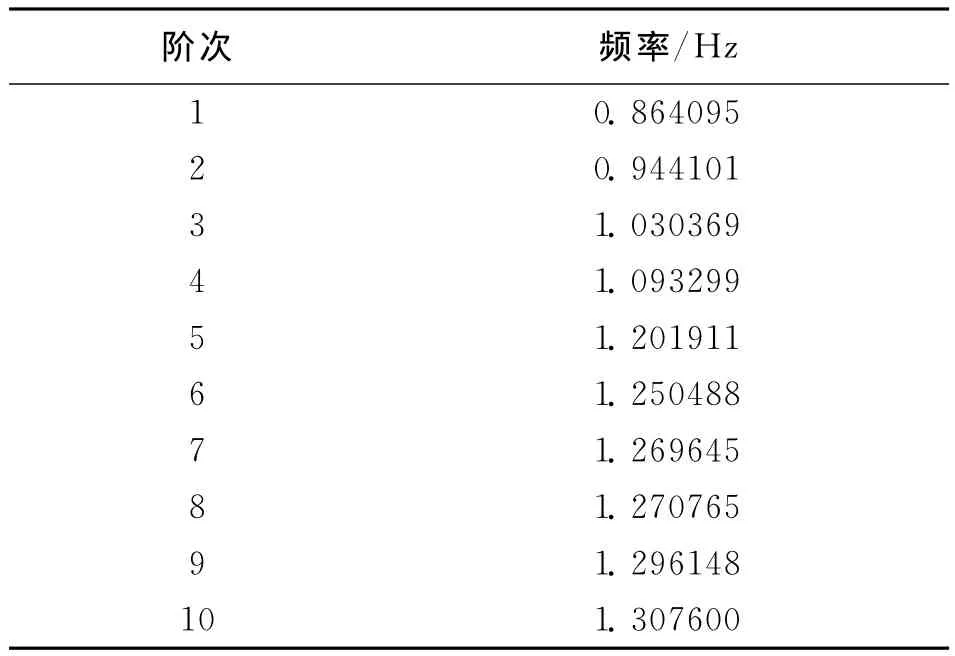
表1 自振频率表

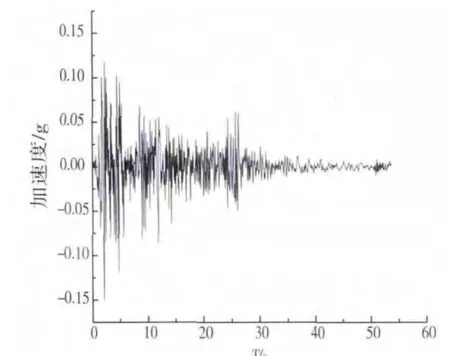
图2 El－Centro波时程曲线

2.4 动力特性

采用多重Ritz向量法求解，取桥梁前10阶振型.按照规范中的规定：总的振型参与质量系数在90%以上，对建立的有限元模型进行自振特性的计算.得到的前10阶自振频率如下表1.

3 非一致地震作用下地震反应时程分析

一般情况下，桥梁工程场地地震波的表视波速取大于500m／s比较合适［4］.为了能考虑到深厚覆盖土层的特殊情况，本文地震行波视波速取为2000m／s、1000m／s、500m／s和250m／s.假定地震波的传播方向与桥梁的顺桥向方向一致，经过地震反应时程分析，得到不同波速下各墩底的剪力、墩顶位移以及面内弯矩.

分析图3、图4和图5：

（1）与非一致激励相比，一致激励地震作用下各墩底的剪力、墩顶位移以及面内弯矩要小.

（2）随波速的增加，各墩底的剪力、墩顶位移以及面内弯矩都逐渐变小，并趋近于一致激励的情况.

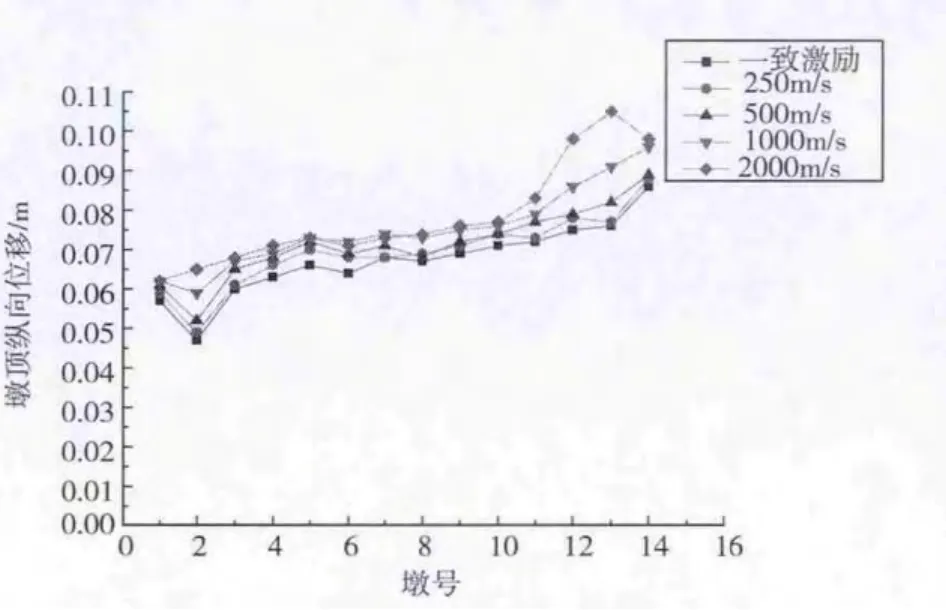
图3 不同波速下墩顶纵向位移图

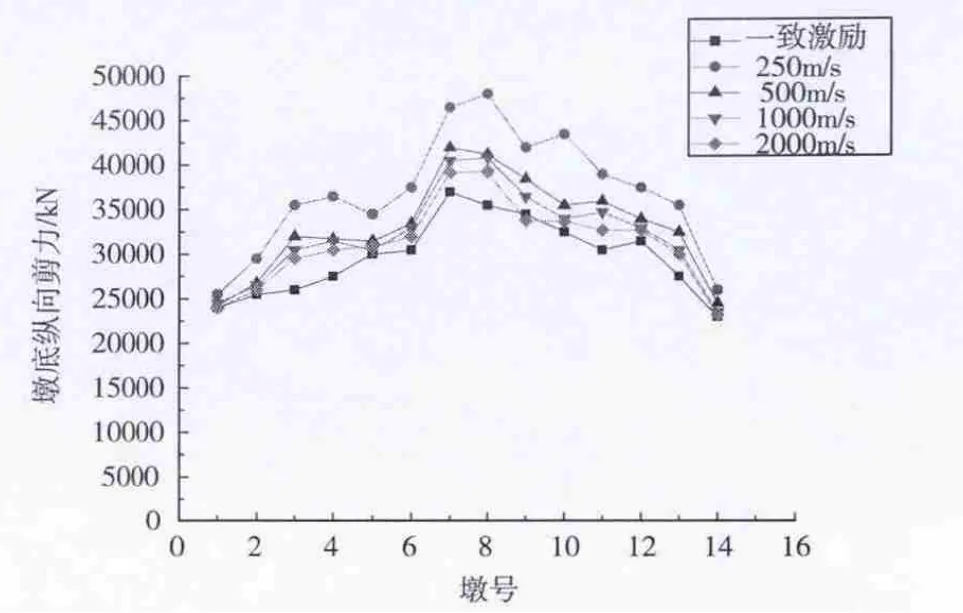
图4 不同波速下墩底纵向剪力图

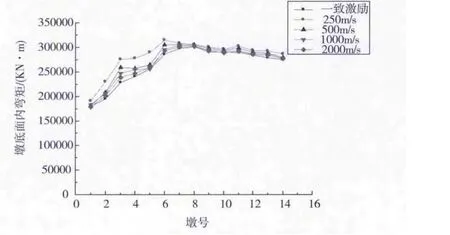
图5 不同波速下墩底面内弯矩图

（3）随着墩号的增加，墩顶的纵向位移有逐渐变大的趋势，墩底的纵向剪力先增大后减小，面内弯矩先增大后趋于平稳.

4 结 论

本文运用有限元软件MIDAS以子牙河特大桥为工程背景建立了有限元模型.采用非一致激励方法，分析了不同波速作用下桥墩墩顶的纵向位移和墩底纵向剪力，主要结论为：

（1）非一致激励的地震作用要比一致激励地震作用的影响要大，对于多跨连续梁桥需要考虑地震的非一致激励情况.

（2）随着波速的增加，非一致激励地震作用下多跨连续梁桥的地震反应逐渐变小.

［1］叶爱君.桥梁抗震［M］.北京：人民交通出版社，2002，9

［2］张静娟.多跨连续梁桥地震行波效应分析［J］.水利与建筑工程学报，2009，7（2）：114～116

［3］王明晔.行波激励下多跨连续梁桥地震反应分析［J］.结构工程师，2007，23（4）：49～54

［4］许莉.非一致地震激励下大跨斜拉桥的地震反应［J］.福州大学学报（自然科学版）.2013，41（4）：528～533

［5］候宇新.大跨斜拉桥地震反应分析［J］.中外公路.2010，，30（2）：127～130