无限时间终端g－期望的Jensen不等式

孙豹

(中国矿业大学理学院，江苏徐州221116)

0 引言

由文献［1］可知，在终端时刻T为有限的情形下，对如下形式的倒向随机微分方程(以下简称BSDE)只要g关于y、z是Lipschitz的，ξ与随机过程g(t，0，0)是平方可积的，那么方程(1)有唯一的一对平方可积的适应解。将式(1)的唯一解记为(Yt(g，T，ξ))，Zt(g，T，ξ)t∈［0，T］)。在对任意(t，y)，g还满足g(t，y，0)=0条件下，S.G.Peng［2］给出了g－期望与条件g－期望的概念。随着这些概念的提出，得到了关于g－期望的很多性质。

文献［3－7］研究了在T＜∞时基于g－期望的Jensen不等式，文献［7］给出了T＜∞，且在Lipschitz条件下基于g－期望的Jensen不等式成立的充分必要条件。近年来，关于T=∞，以及对Lipschitz减弱条件下的BSDE的研究成为重点。文献［4－12］研究了当T=∞时BSDEs的一些基本理论，文献［9］研究了当T=∞时，且非一致Lipschitz下的BSDE的解的存在唯一性，并且推广了g－期望与条件g－期望的概念。笔者在此基础上研究了在非Lipschitz条件下，当T=∞时g－期望的Jensen不等式成立的充要条件。

1 预备知识

设0＜T≤∞，当T=∞时［0，T］=［0，∞)。(Ω，F，P)是一完备的概率空间，(Bt)t≥0是d维布朗运动，B0=0，设(Ft)t≥0是由此布朗运动生成的自然σ域流，

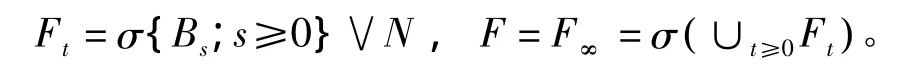
式中N为由所有P零测度集组成的子集类。

文中总假定在概率空间(Ω，FT，P)上研究问题，现给定一些记号:

L2(Ω，Ft，P):{ξ:ξ是Ft可测的随机变量且满足E［ξ2］＜∞}。

考虑下列形式的一维倒向随机微分方程:

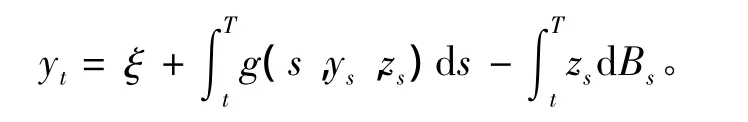
T为终端时刻可以为有限或者无限，倒向随机微分方程生成元函数g为

且对任意的(y，z)∈(R×Rd)，(g(t，y，z))t∈［0，T］是循序可测过程，并且g满足下列条件:

(H1)g关于(y，z)满足对t非一致的Lipschitz条件，即存在两个定义在［0，T］上的正值确定性函数u(x)和v(x)满足，且使得dp×dt－a.s.，

(H3)对dt－a.e.，t∈［0，T］，存在两个常数δt＞0和Kt＞0，

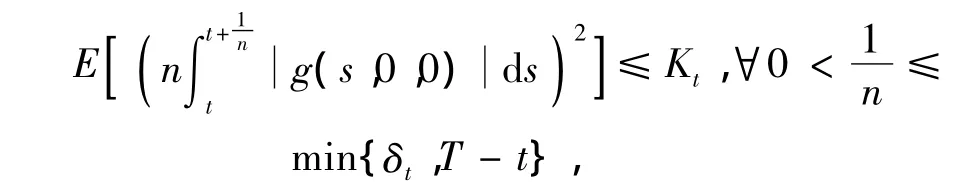
下面给出的定义1和2中，均假设g满足(H1)和(H4)。

定义1［9］(g－期望)εg［ξ］:L2(Ω，FT，P)→R，定义εg［ξ］=Y0(g，T，ξ)。

定义2［9］(条件g－期望)ξ关于Ft的条件g－期望定义为

在以下引理中，均假设g满足(H1)和(H4)。

引理1［9］(1)(保常性)εg［c］=c，∀c∈R;

(2)(单调性)εg［X1］≥εg［X2］，如果X1≥X2，a.s.;

(3)(严格单调性)εg［X1］＞εg［X2］，如果X1≥X2，a.s.，且P(X1＞X2)＞0。

引理2［9］(1)如果X是Ft可测的，那么εg［X Ft］=X;

(2)对任意t∈［0，T］，有εg［εg［XFt］］=εg［X］。

引理3［9］)中满足式(2)的唯一的随机变量η，

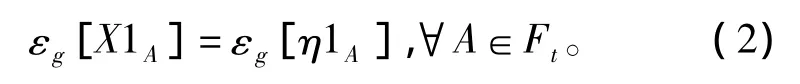
引理4［9］假设g满足(H1)和(H3)，如果g不依赖于y，则

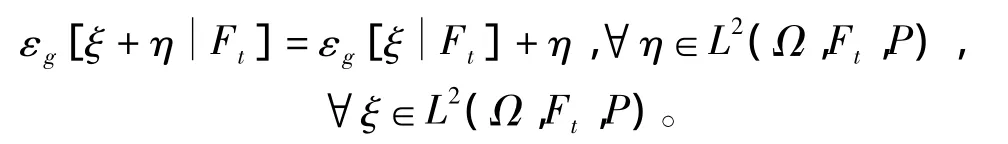
注1非一致Lipschitz条件下，文献［9］给出了引理1～4的证明，文中不再证明。

引理5［13］0＜T≤∞，令g满足(H1)和(H2)，且1≤p＜2，则对任意(y，z)∈R×Rd如式(3)对t∈［0，T］中几乎所有的t都成立，

2 主要结果

设g满足条件(H1)、(H2)和(H3)，(y，z)∈R×，记

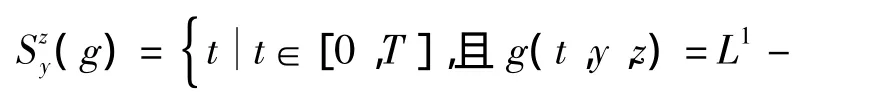
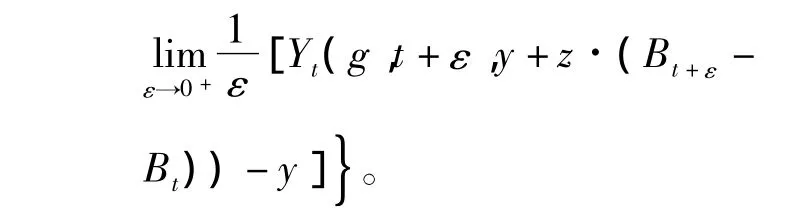
如果g不依赖于y，那么记

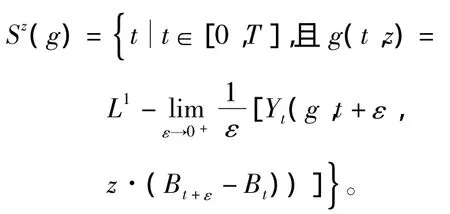
定理1设生成元g满足条件(H1)、(H2)和(H3)。

(i)如果对∀0≤t＜T，0＜ε≤T－t，∀a，b，y∈R，z∈Rd，有a.s.，

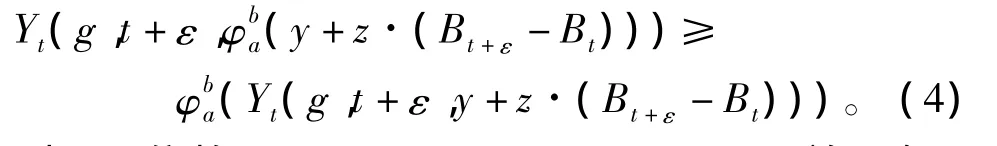
则g不依赖于y，g(t，0)=0，dP×dt－a.s.并且有

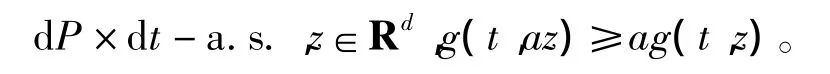
进一步，如果设g也满足(H4)，则以下两个条件等价:

(ii)g不依赖于y，且dP×dt－a.s.，z∈Rd，g(t，az)≥ag(t，z)。

(iii)对∀a，b∈R，ξ∈L2(Ω，FT，P)，有εg［aξ+b］≥aεg［ξ］+b。

证明(i)对任意t∈［0，T］，y∈R，z∈Rd，足够大的正整数n，满足，由式(4)有P－a.s.，

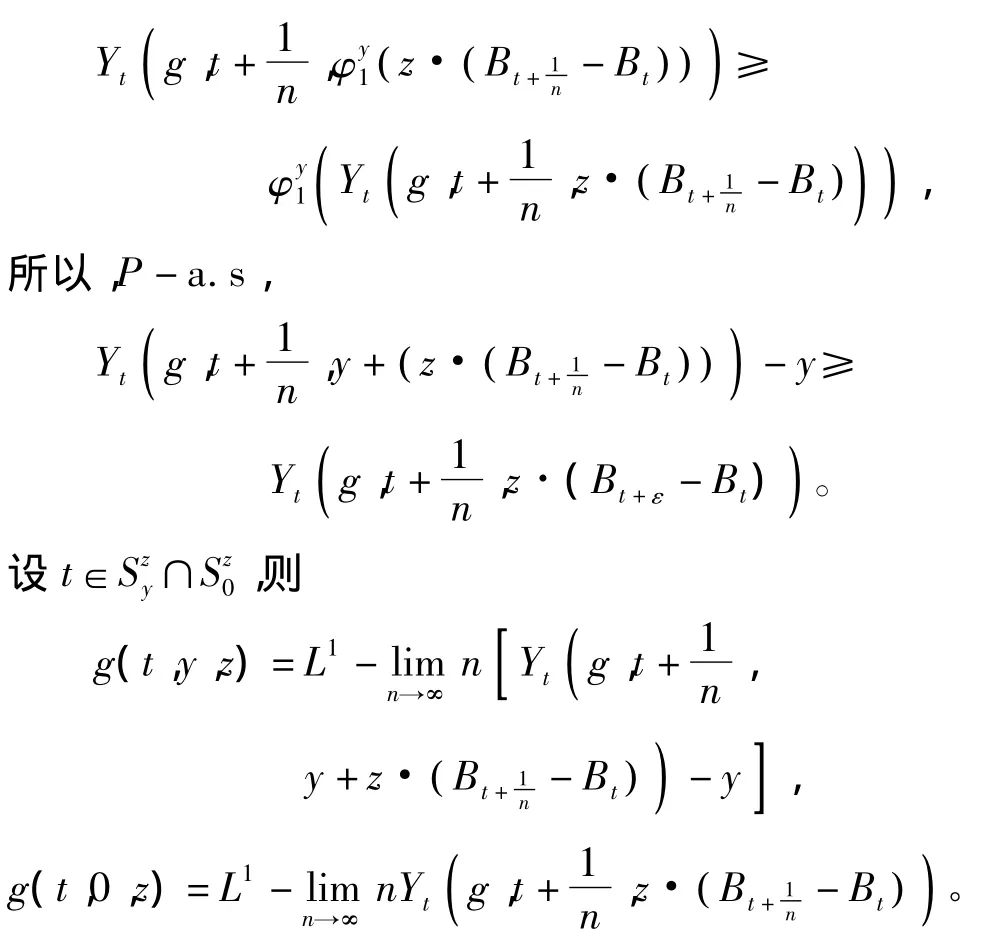
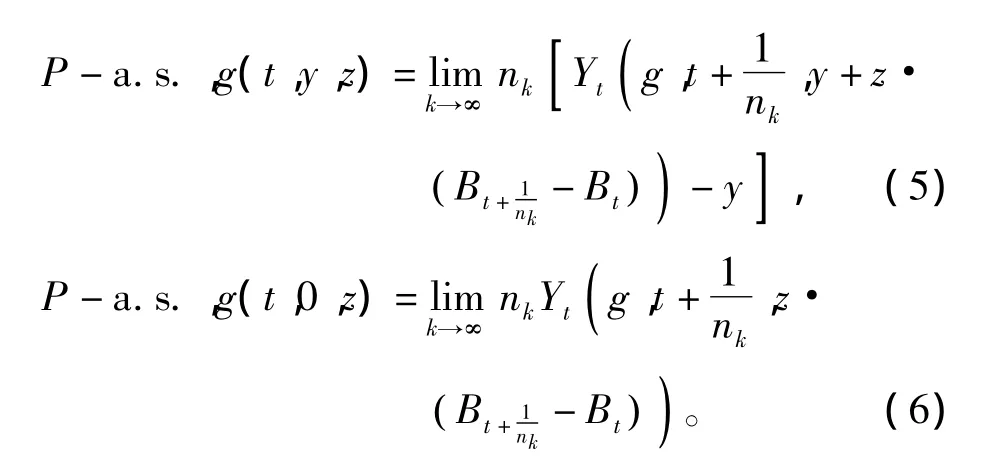
P－a.s.，g(t，y，z)≥g(t，0，z)。

由引理5(表示定理)对几乎处处的t成立，可知λ(［0，T］/∩)=0，因此对每个y∈R，z∈Rd，有

dP×dt－a.s.，g(t，y，z)≥g(t，0，z)。由(i)可知

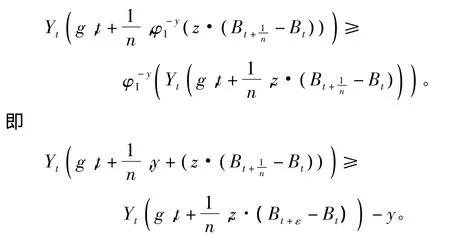
用相同的方法可证得

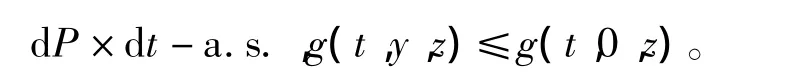
所以对任意y∈R，z∈Rd，有

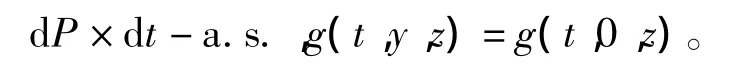
又因为g对y满足非一致Lipschitz的，所以对任意z∈Rd，有

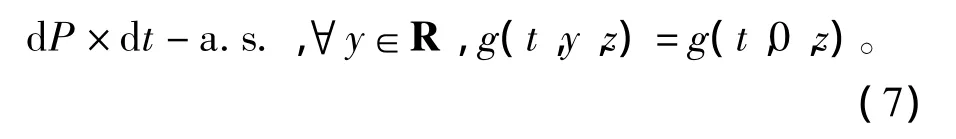
因此，由式(7)可知，g是独立于y的。

类似于文献［7］中的方法，可以证明g是关于z是超奇次的，即

(ii)⇒(iii)，若g满足条件(H1)、(H2)、(H3)和(H4)且

则

证明对ξ∈L2(Ω，FT，P)，令(yt，zt)t∈［0，T］为BSDE(8)的解:

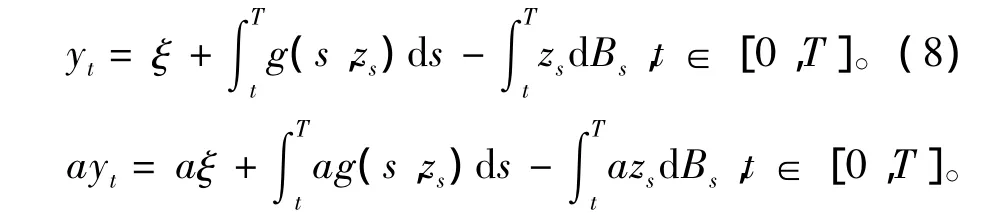
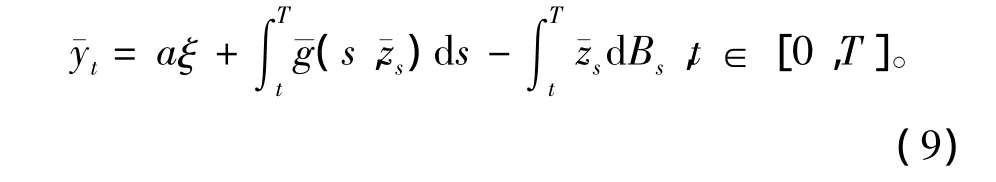
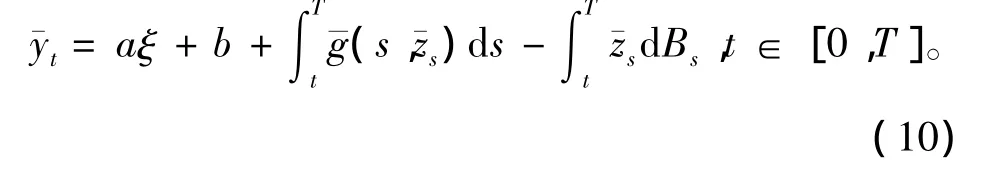
考虑式(10)、(11)，因为∀a∈R，g(t，az)≥ag(t，z)，即有g(t，z)≥(t，z)。所以由比较定理知

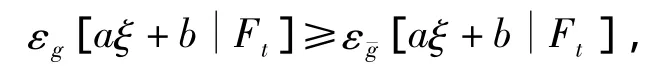
即

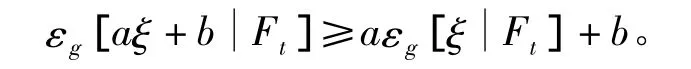
特别的∀a∈R，ξ∈L2(Ω，FT，P)，有

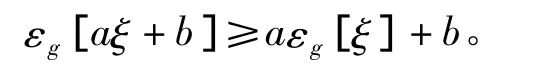
(iii)⇒(ii)，由(i)的证明过程可知显然成立。

注2定理1中关于g的条件若满足条件(H4)，则必然满足条件(H2)和(H3)，那么g只要满足条件(H1)和(H4)就可以得到(iii)⇔(ii)。

注3若g满足条件(H1)、(H4)，则(ii)和(iii)与(iv)等价。

(iv)基于g－期望的Jensen不等式关于一般的凸函数φ成立，即对任意ξ∈L2(Ω，FT，P)，凸函数φ:R→R，如果φ(ξ)∈L2(Ω，FT，P)，则

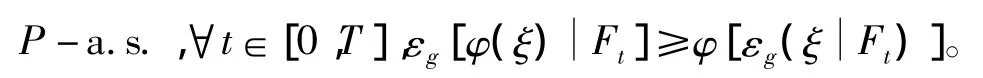
显然(iv)⇒(iii)，(ii)⇒(iv)的证明过程可参照文献［7］中的证明方法。

［1］ PAEDOUX E，PENG S G.Adapted solution of a backward stochastic differential equation［J］.Systems＆Control Letters，1990，14(1):55－61.

［2］ PENG S G.Backward SDE and related g-expectation［C］//El KAROUI N，MAZLIAK L.Backward stochastic Differential Equations.Pitman Research Notes Mathematical Series，Longman，Harlow，1997，364:141－159.

［3］ CHEN Z J，KULPERGER R，JIANG L.Jensen’s inequality for g-expectation:part 1［J］.Comptes Rendus Mathematique，2003，337(11):725－730.

［4］ CHEN Z J，KULPERGER R，JIANG L.Jensen’s inequality for g-expectation:part 2［J］.Comptes Rendus Mathematique，2003，337(12):797－800.

［5］ FAN SHEGJUN.Jensen’s inequality for filtration consistent nonlinear expectation without domination condition［J］.Journal of Mathematical Analysis and Application，2008，345(2):678－688.

［6］ FAN SHENGJUN.A note of Jensen’s inequality for BSDEs［J］.Acta Mathematica Sinica:English Series，2009，25(10):1681－1692.

［7］ JIANG LONG.Jensen’s inequality for backward stochastic differential equations［J］.Chin Ann Math，2006，27B(5):553－564.

［8］ ZHANG HENGMIN，FAN SHENGJUN.A representation theorem for generators of BSDEs with finite or infinite time intervals and linear-growth generators［J］.Statistics and Probability Letters，2013，83(3):724－734.

［9］ CHEN ZENGJING，WANG BO.Infinite time interval BSDEs and the covergence of g-martingales［J］.J Austral Math Soc:Series A，2000，69(2):187－211.

［10］ FAN SHENGJUN，JING LONG，TIAN DEJINA.One-dimensional BSDEs with finite and infinite time horizons［J］.Stochastic Processes and their Applications，2011，121(3):427－440.

［11］ FAN SHENGJUN，JANG LONG.Finite and infinite time interval BSDEs with non-Lipschitz coefficients［J］.Statistics and Probability Letters，2010，80(11/12):962－968.

［12］ ZHANG QI，ZHAO HUAIZHONG.Stationary solutions of SPDEs and infinite horizon BDSDEs with non-Lipschitz coefficients［J］.Journal of Differential Equations，2010，248(5):953－991.

［13］ 朱开永，范胜君，吴祝武.基于g－期望的收敛定理［J］.云南大学学报:自然科学版，2009，31(3):227－231.