基于NLFM的超低旁瓣脉冲压缩方法研究

(电子科技大学电子工程学院,四川成都611731)

0 引言

在现代雷达系统中,一方面,为了提高雷达的探测距离,我们希望能够发射峰值功率大的信号,而探测距离的增大,又会使雷达的距离分辨率下降,所以为了缓和雷达的探测距离和距离分辨率之间的矛盾,脉冲压缩技术由此得到了很广泛的应用。

常用的脉压信号主要有线性调频信号和非线性调频信号。线性调频信号易于产生和实现,但是其脉冲压缩之后的旁瓣过高,其主副瓣比最大只能达到-13.2 dB,这在多目标检测中是很不利的,因为微弱信号的主瓣很可能被强目标的旁瓣给淹没,从而造成目标的漏检和误检。因此必须采取措施降低脉压信号的旁瓣电平,传统的抑制旁瓣的方法主要有时域或频域加权法,加权函数一般采用窗函数。但是加权会引起信噪比损失和主瓣展宽等一系列问题,而且加权之后的脉压输出也只能获得-40 dB左右的主副瓣比,根本无法满足许多雷达系统的需要。非线性调频信号由于直接匹配脉压输出就能得到较低的主副瓣比,所以现在被广泛研究。但是在某些新型的天气雷达中,一般地杂波的反射强度能比雨水高30～55 dB[1],为了测量雨水的强度,就要求脉压之后的归一化旁瓣至少在-60 d B以下。因此,进一步降低脉冲压缩输出信号的旁瓣电平,是脉压技术中一项非常重要的任务。

为了压制强的杂波,本文在传统的相位逗留法[2]设计非线性调频信号的基础上,提出了一种改进的方法,也就是将非线性调频信号与一个改进的幅度函数进行加权,然后利用加权之后的信号进行脉冲压缩,仿真结果表明,该方法能够有效地抑制旁瓣。不过由于引入了窗函数加权,所以造成了一定的信噪比损失。

1 用相位逗留法设计的非线性调频信号

假设非线性调频信号的表达式为

式中,a(t)为信号的幅度函数,φ(t)为信号的相位函数。一般情况下,为了使发射信号的能量足够大,都是假设信号的幅度具有矩形形状,即a(t)=1,所以非线性调频信号的表达式可以简写为

由式(2)可知,设计非线性调频信号只需设计出信号的相位函数即可。根据相位逗留理论,非线性调频信号的设计都是基于窗函数反求法来得到的。也就是说,使脉压输出信号的频谱等于一个理想的窗函数：

式中,W(f)为窗函数的表达式,|S(f)|2为匹配输出信号的频域表达式。由此可得到信号的群时延表达式为

式中,K为一个常数,其表达式为

对群时延函数求反函数,可以得到信号的频率函数f(t),其表达式为

根据已知的频率函数,可以求出相位函数：

将相位函数代入式(2),则可以得到非线性调频信号。

设仿真条件为T=40μs,B=5 M Hz,Fs=4B,则仿真结果如图1～4所示。

从图4可以看出,传统的相位逗留法设计的非线性调频信号进行脉冲压缩之后的主副瓣比只能达到-40dB左右,因此为了满足雷达系统的需要,进一步地降低信号的旁瓣是必须的。在此基础上,其他降低信号旁瓣的方法被提出。

图1 群时延函数

图2 频率函数

图3 相位函数

图4 匹配脉压之后的输出波形

2 幅度加权窗函数的设计

假设非线性调频信号的表达式为

式中,a(t)为幅度调制函数,φ(t)为相位调制函数,则信号的傅里叶变换可以表示为

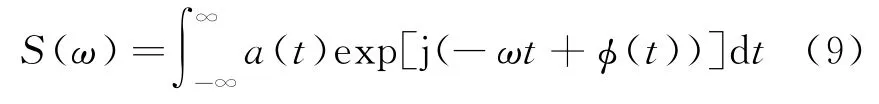
由于φ(t)是一个未知的复合函数,所以这个积分难以求解,除非相位函数φ(t)像线性调频信号的相位函数那样简单。所以我们假设跟相位相比a(t)变化缓慢,因此通过相位逗留原理可以得到一个渐进性逼近的结果。由相位逗留原理可知,假设相位函数φ(t)仅在t=t0处有一个相位逗留点,则有φ′(t0)=0,将相位函数φ(t)在t=t0处按照泰勒级数进行展开,并取前三项,则可以得到

将此表达式代入到S(ω)中,可得

又由于有泊松公式

通过利用泊松公式,可将S(ω)化简为

所以得到的幅度函数为

由于幅度函数已知,所以功率谱密度为

因此,为了计算幅度函数a(t),所需的功率谱的形状必须指定。由于许多常用的窗函数是由一系列cos函数的和组成的,所以功率谱可以表示为

将式(16)代入式(15),则幅度函数a(t)可以表示为

假设使用的窗函数为高斯窗[3],其表达式为

则要求幅度函数a(t)的表达式,只要再将相位函数确定下来即可。

通过文献[4]可知,相位函数由sinω和tanω的组合能够取得不错的效果。因为它们能够取得相当高的加权效率并且仅仅需要相当简单的计算。迄今为止一个比较好的组合是将一个线性函数和一个正切-线性函数进行组合,也就是说

式中,常数γ控制tanx曲线的比例;α控制tan-FM和LFM之间的平衡;B为信号的带宽;t在-T/2～T/2之间取值;φ′(t)为基带调制信号的相位调制函数的一阶导数。在实际仿真过程中,由于α和γ没有特定的取值范围,所以要想取得比较好的脉压效果,就必须进行大量的仿真实验来确定这两个参数的取值。

由于φ′(t)已知,所以对其求关于t的导数,则可以得到φ″(t),其表达式为

通过仿真可知,当α的值太小时,调频函数变成线性的;当α和γ的值较高时,调频函数逼近S型,并且a(t)变得更像矩形,可以得到更低的加权损失。所以为了获得更好的脉压,大量的仿真实验是必须的。

由于相位函数在t0点的导数为零,所以根据S(ω)的表达有[-ωt+φ(t)]′=0,也就是ω=φ′(t),所以将ω用φ′(t)替换掉,则幅度加权函数a(t)的表达式可以改写为

由于a(t)和φ(t)都已经确定了,所以非线性调频信号s(t)可以表示为

根据式(22)可以将信号s(t)确定,然后用这个信号进行脉冲压缩即可。

3 仿真结果

设仿真条件为T=40μs,B=5 MHz,Fs=4B,α=0.88,γ=1.36,则仿真结果如图5～8所示。

图5 非线性调频信号的频率函数

图6 非线性调频信号的相位函数

图7 振幅窗与Hamming窗的频谱对比

图8 匹配脉压仿真结果

图5 为信号频率函数,从图中可以看出,通过选取合适的参数α和γ,其仿真输出波形基本与S型曲线接近;图6为信号相位函数;图7为本文设计的振幅窗函数与汉明窗的对比,从图7可以看出,本文设计的振幅窗函数相比Hamming窗性能要好,因为它更接近矩形窗,所以在同等条件下,该窗所能包含的能量更多,雷达所能探测到的距离更远。图8为将非线性调频信号与改进的窗函数进行加权之后再脉冲压缩的结果,从图中可以看出输出信号的主副瓣比为-73 dB,通过对比没有加权之前的脉压结果,可以得到主瓣展宽1.6倍,由于加权不可避免地会导致信噪比的损失,通过计算可以知道其信噪比损失为0.789 1 d B,也就是说这种方法相当于是利用信噪比损失换取主副瓣比的提高。但是在实际应用中,为了达到所要求的主副瓣比,就不得不在信噪比损失上作出妥协。因此在设计过程中,必须在信噪比损失和主副瓣比之间作出折中。

下面将加权的非线性调频信号进行脉冲压缩的结果与加权的线性调频信号进行脉冲压缩的结果作一个对比,其中主要涉及到了Hamming窗、Hanning窗以及Blackman窗[5],仿真条件一致,其结果如表1所示。

表1 不同窗函数的性能对比

从表1可以看出,通过与线性调频信号进行对比,虽然线性调频信号易于产生与实现,但是它的脉压效果却不是很好,Blackman窗虽然可以很好地抑制旁瓣电平,但是信噪比损失很大,并且主瓣宽度展宽很多,通过对比可以发现,虽然利用本文的方法得到的主副瓣比不是最低的,但是它的主瓣展宽最小,信噪比损失最少,所以在这几个参数之间进行权衡的话,其最终的效果还是比较理想的。

4 结束语

本文针对现代雷达系统对低旁瓣的需求,在综合考虑主副瓣比、信噪比损失、主瓣展宽等因素的基础上,通过设计一个振幅窗函数,然后将非线性调频信号与振幅窗函数进行结合,将这个新产生的信号进行脉冲压缩,仿真结果表明,可以获得-73 dB的主副瓣比,不过由于幅度加权的原因,还是引入了一定的信噪比损失,但是对比没有幅度加权的情况下,主副瓣比只能达到-40 d B左右,远远不能满足星载降水雷达的需要,所以综合考虑各方面因素还是值得的。

虽然本文的方法将副瓣电平得到了很好的抑制,但是由于加权不可避免地会导致信噪比损失,所以其性能还不是太好,因此还有待于进一步的深入研究。

[1]YIN Hong-gang,DONG Xiao-long.Pulse Compression with Ultra-Low Range Sidelobe for Space-Borne Meteorology Radars[C]//International Conference,[S.l]：[s.n.],2008：769-798.

[2]LUO Feng,RUAN Liting,WU Shunjun,et al.Design of Modified Spectrum Filter Based on Mismatched Window for NLFM signal[C]//2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar,Xi’an,China：[s.n.],2009：274-277.

[3]GE Zhiqiang,HUANG Peikang,LU Weining.Matched NLFM Pulse Compression Method with Ultra-Low Sidelobes[C]//Proceedings of the 5th Radar Conference,Amsterdam：IEEE,2008：92-95.

[4]COLLINS T,ATKINS P.Nonlinear Frequency Modulation Chirps for Active Sonar[J].IEE Proceedings Radar,Sonar and Navigation,1999,146(6)：312-316.

[5]蒋锋,李石.线性调频和非线性调频的信号脉压分析[J].电子元器件应用,2010,12(7)：72-74.

[6]李少东,裴文炯,杨军.基于CS的LFM信号脉冲压缩实现算法研究[J].雷达科学与技术,2013,11(3)：295-301.