双波段模式下的雷达数据处理系统设计

韩 伟,何彦杰,李 智,肖 卉

(1.95980部队,湖北襄阳441100;2.空军预警学院空天基预警监视装备系,湖北武汉430019)

0 引言

双波段雷达与单波段雷达相比具有如下优势：(1)能以更高的检测概率发现目标甚至隐身目标;(2)抑制角闪烁,提高角度跟踪精度;(3)抗干扰性能强[1-3]。而两面阵雷达[4]具有全方位空域探测、作战飞机引导、精确目标定位和指示、防御高俯冲和略海飞行的反舰导弹的能力,成为舰载雷达的主要形式[5-6]。本文则将两种雷达的优势进行结合,从提高跟踪精度的角度设计了一种背靠背式两面阵双波段雷达天线,用于机载预警雷达。两面阵天线分别发射不同频率电磁波,采用机械扫描模式,且两个阵面有独立的收发系统,形成两个通道分别工作,在时间上交替产生目标点迹,形成点迹数据流。与时间对准下的并行处理数据融合[7-8]不同,本文对两面阵点迹数据进行串行合并处理,可以使数据率加大,这意味着跟踪精度提高,航迹连续性更好。另外,由于数据率提高,使航迹起始速度加快,并易于跟踪,提高了反低空突防和低空反导的能力[9-11]。实际上,天线阵面和处理通道会受各种环境因素的影响,其测量误差变大,严重影响跟踪精度,文献[12]对该影响进行了详细的分析,但主要是针对两个通道的目标参数测量误差相等的情况。由于采用双波段体制,两个通道的测量误差是有差异的,虽然串行合并式处理提高了目标的跟踪数据率,但低精度的测量误差会降低目标整体的跟踪精度,使得目标跟踪精度在数据率提高的情况下仍有可能下降。因此,从理论上研究数据率和通道测量误差如何影响目标跟踪精度成为两面阵双波段雷达工作过程中面临的一个重要问题。在此基础上,从总滤波次数的选择和双波段的配置两个方面设计两面阵双波段雷达数据处理系统也具有十分重要的意义。

本文针对某一种典型的目标运动模型,首先从理论上分析了点迹串行合并条件下测量误差和滤波迭代次数对Kalman滤波性能的影响,然后针对不同情况,给出了两面阵双波段雷达数据处理系统的设计原则,最后应用蒙特卡洛仿真试验来验证理论分析结果和系统设计的正确性。

1 双波段集中式目标跟踪性能

1.1 机载预警雷达双波段天线模型

本文基于一种构建的背靠背式双波段雷达开展目标跟踪技术研究。两个天线阵面分别发射不同波段的电磁波,由于机械扫描可在空域中提供360°无缝覆盖范围,故采用机械扫描的方式,两个阵面同时旋转。天线示意图如图1所示。根据机载预警雷达的相关任务和工程实现性,双波段雷达可以有UHF/L,UHF/C,UHF/S,L/C,L/S,C/S等频率配置。

图1 两面阵双波段天线示意图

两面阵双波段雷达的数据处理与单面阵不同,必须具有两面阵数据融合功能,主要分为并行式处理和串行合并式(集中式)处理。并行式处理为航迹级相关融合,即两个阵面分别录取跟踪数据形成航迹后再进行相关处理,这种方法相对容易但不能体现出背靠背双通道的优势。串行合并式对两面阵数据按时间顺序组合成类似单雷达的探测点迹,用于点迹-航迹互联,并形成相应的航迹,这种方法具有高数据率,充分利用双通道的优势,因此,本文针对该融合方法进行研究。串行合并式的一个显著特点是合成后的数据流的数据加大,这意味着跟踪精度的提高,尤其是在目标发生机动的情况下。另外,由于总体数据率提高,使得航迹起始速度加快,这对于反低空突防和低空反导尤为重要。

设第i个波段的探测周期为T i,则双波段系统的平均探测周期为

从式(1)可知,当T1=T2时,数据率有最大的提高。当T1=T2=6s,则T=3s,数据率提高了1倍;而当T1=6s,T2=12s,数据率仅提高0.5倍,因此最好使两个波段的数据率相同,即有相同的扫描周期,本文后面的分析采用相同的扫描周期。

1.2 基于串行合并式的数据融合跟踪性能分析

设其中一个波段的量测噪声方差为σ2n,另一波段为rσ2n。其中,r为测量噪声方差比,且r＞1,两个波段交替工作。两个面阵的采样周期均为T,双波段集中式的采样周期为T′,在背靠背式机械扫描天线的背景下,假设T=2T′。在不影响分析结果的情况下,这里以位置、速度二维状态系统为例进行分析,目标运动模型为CV模型,观测矩阵与状态转移矩阵分别表示如下：

式中,Φ和Φ′分别为单通道和双通道跟踪条件下的状态转移矩阵。假设初始时刻k=0时,高精度通道、低高精度通道和双波段双通道串行合并条件下的滤波误差分别表示为

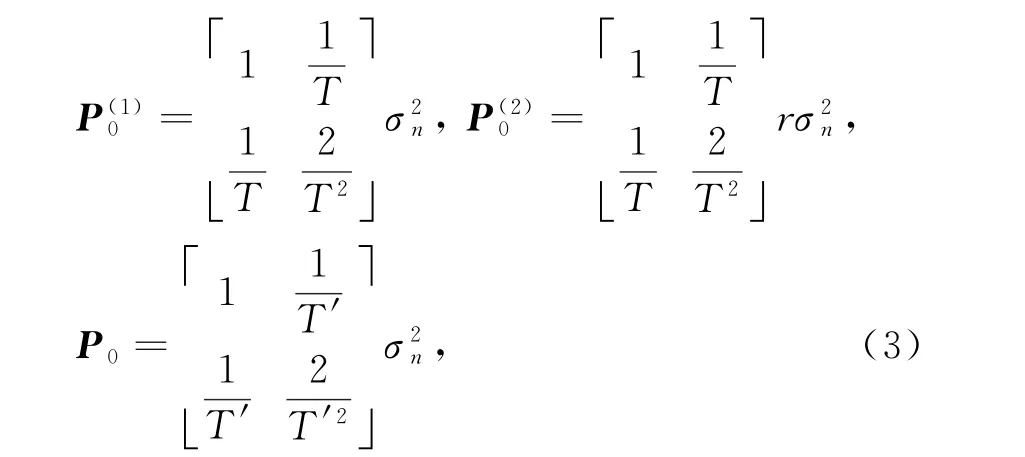
则高、低精度通道的滤波误差递推式可分别为

双通道串行合并条件下的滤波误差递推式为

高、低精度单通道和双波段双通道串行合并式的点迹流及时间对应关系如图2所示。将测量噪声方差比r取为9,对式(3)和式(5)进行数值计算,得到位置滤波误差随滤波次数的变化情况,如图3所示。这里的数据采样间隔为1/2帧。可以看到,双波段串行合并式滤波的位置误差呈现锯齿状。在采用高精度数据进行滤波迭代时,误差变小,位于锯齿下方,而采用低精度数据进行滤波迭代时,误差突然变大,位于锯齿上方。从局部放大图4(a)可以看出,在滤波迭代到第8步时,双波段跟踪的位置滤波误差开始部分小于高精度位置滤波误差。从局部放大图4(b)可以看出,在滤波迭代到第37步时,双波段跟踪的位置滤波误差开始整体小于高精度位置滤波误差。我们将以上两个时间点分别用K1x和K2x表示。

为比较双通道点迹串行合并与单通道的跟踪性能,定义如下指标因子[13]：

式中的除法为矩阵对应元素相除,A(k)为相同时刻双通道串行合并式的滤波误差P k与高精度通道滤波误差P(1)k对应元素的比值,a11和a12分别为位置和速度滤波误差比值,当它们小于1时,表明双通道串行合并式的滤波误差小于高精度通道,即双波段跟踪精度满足最低精度要求。

指标因子A(k)体现的是双通道串行合并与高精度单通道在对应时刻的跟踪性能对比情况,但该指标不能体现双通道在低精度通道对应时刻的跟踪性能情况,基于此,定义另一个指标因子如下：

B(k)为低精度时刻双通道串行合并式的滤波误差P k与前、后高精度时刻滤波误差的均值(+)/2对应元素的比值,b>11和b22分别为位置和速度滤波误差比值,当它们小于1时,表明双通道串行合并式的滤波误差整体小于高精度通道。

图2 点迹流的时间对应关系

图3 位置滤波误差

图4 位置滤波误差局部放大图

实际上,双波段滤波误差整体小于高精度滤波误差的时间点对雷达的实际应用很重要。对于机载预警雷达上的机械式扫描天线而言,其扫描周期一般为10 s左右,如果该时间点较晚,则不利于现代复杂多变战场环境下的信息化作战。基于此种考虑,需要分析在不同波段的配置下时间点的位置。

结合双波段雷达配置的实际情况,将测量噪声方差比r从1取到100,计算得到双波段位置滤波误差部分小于高精度时刻K1x、双波段速度滤波误差部分小于高精度时刻K1v、双波段位置滤波误差整体小于高精度时刻K2x和双波段速度滤波误差整体小于高精度时刻K2v随r的变化情况如图5和图6所示。4个时刻点均随着r的增大而增大,即两波段精度差别越大,跟踪滤波性能改善所需的时间越长。从图5可以看出,当r=100时,需要滤波迭代32次才能使得双波段位置滤波误差部分小于高精度波段,以双波段采样周期T2=5 s来计算,则需要经过160 s才能满足要求,这满足实际作战的需求。但是当误差部分低于高精度时,仅在高精度对应时刻采样,这显然没有充分利用双波段高数据率的优势。因此,还须将双波段所有的数据信息利用上,这就需要找到双波段位置滤波误差整体小于高精度的时刻。如图6所示,以雷达第60帧为最大时间点,则r应小于30。这意味着配置两个波段时,仅考虑位置滤波误差条件下,如果其中一个波段选定,另一个波段的精度与其相差不超过30倍。从图5和图6还可以看到,在r相同条件下,K1v＞K1x,K2v＜K2x,这表明双波段速度滤波误差部分小于高精度的时刻要晚于位置滤波误差相应的时刻,双波段速度滤波误差整体小于高精度的时刻则要早于位置滤波误差相应的时刻。

图5 双波段滤波误差部分小于高精度的时刻

图6 双波段滤波误差整体小于高精度的时刻

1.3 数据处理系统设计

在对双波段数据处理系统进行设计时,需要考虑两个方面的问题：①在给定的跟踪时间内,如何配置两个波段,即设计测量噪声方差比,才能保证双波段跟踪精度较单波段有所改善;②在测量噪声方差比确定的情况下,需要经过多少次迭代滤波,才能保证双波段跟踪精度较单波段有所改善。

针对问题①的设计：

由图5可知,当滤波次数最多为20次时,要使得a11＜1,测量噪声方差比r应小于48,要使得a22＜1,测量噪声方差比r应小于17,综合考虑,系统设计时r应小于17。由图6可知,当滤波次数最多为20次时,要使得b11＜1,测量噪声方差比r应小于6,要使得b22＜1,测量噪声方差比r应小于5,综合考虑,系统设计时r应小于5。

针对问题②的设计：

由图5可知,当测量噪声方差比r设为9时,要使得a11＜1,至少需要进行8次滤波,即K1x=8,要使得a22＜1,至少需要进行16次滤波,即K1v=16;由图6可知,当测量噪声方差比r设为9时,要使得b11＜1,至少需要进行37次滤波,即K2x=37,要使得b22＜1,至少需要进行35次滤波,即K2v=35。

基于以上分析,可以为双波段数据处理设计出相应的工程应用方法,具体规则如下：

(a)如果优先考虑目标位置状态,则将K1x和K2x定为两个分界点时刻,即在时刻K1x之前采用高精度波段数据,在K1x到K2x时段,采用双波段在高精度对应时刻的采样数据,在K2x以后采用双波段的所有数据。

(b)如果优先考虑目标速度状态,则将K1v和K2v定为两个分界点时刻,即在时刻K1v之前采用高精度波段数据,在K1v到K2v时段,采用双波段在高精度对应时刻的采样数据,在K2v以后采用双波段的所有数据。

(c)如果需对两种状态综合考虑,则将K1v和K2x定为两个分界点时刻,即在时刻K1v之前采用高精度波段数据,在K1v到K2x时段,采用双波段在高精度对应时刻的采样数据,在K2x以后采用双波段的所有数据。

根据上述的规则,可以对系统的数据处理模式进行设计。数据处理系统结构如图7所示,k=0,2,…,2N,N为非负整数。

图7 数据处理系统结构

当优先考虑位置状态时,t1=K1xT,t2=K2xT;当优先考虑速度状态时,t1=K1vT,t2=K2vT;当综合考虑两个状态时,t1=K1vT,t2=K2xT。

2 仿真实验

为了验证跟踪滤波性能理论的正确性和数据处理系统的有效性,设置仿真环境如下：目标在x轴方向上作匀速直线运动,初始状态为(300 m,10 m/s),量测噪声为零均值高斯白噪声,波段1(高精度)和波段2(低精度)的量测噪声方差σ2n分别为104m2和r×104m2,r为测量噪声方差比。分别利用高精度通道、低精度通道和双波段集中式进行Kalman滤波。假设单波段的采样周期T1为10 s,双波段串行合并式处理的采样周期T2=5 s。单波段滤波次数为50,双波段串行合并式滤波次数为100,Monte Carlo仿真次数为5 000次。设目标在k时刻的真实状态为(x k,k),滤波值为为,则目标位置和速度滤波误差方差可表示为

式中,N为蒙特卡洛次数。指标因子A(k)和B(k)可以根据σ2k,x和σ2k,̇x来计算。这里,以A(k)为分析指标。

首先,确定r,验证使双波段跟踪滤波精度满足最低要求所需的最小滤波迭代次数。这里,r取9。图8表示高、低精度通道和双波段集中式滤波得到的位置滤波误差方差。图9表示b11随滤波迭代次数的变化情况,由图9可知,在r=9的条件下,如果K2x≥37,则b11＜1,这与图6给出的理论分析是一致的。

图8 位置滤波误差

图9 b11随滤波迭代次数的变化情况

然后,在给定滤波次数的条件下,验证使双波段跟踪滤波精度满足最低要求所需的r值范围。这里,滤波迭代次数取为20。图10表示在低精度采样时刻,高精度通道和双波段集中式滤波误差随r的变化情况。两者误差的对比可以反映双波段集中式滤波误差整体小于高精度的条件,由此可以得到如图11所示的b11随r的变化情况。由图11可知,在滤波次数为20的条件下,如果r＜6,则b11＜1。这与图6给出的理论分析是一致的。

图10 位置滤波误差随r的变化

图11 b11随r的变化情况

3 结束语

本文以背靠背式双波段两面阵机载预警雷达为平台,针对目标跟踪问题,从理论上分析了高、低精度通道和双波段集中式的滤波误差,并由此导出了测量噪声方差和滤波迭代次数对跟踪性能的影响,然后从两个波段的配置和总滤波迭代次数两个方面,给出了两面阵双波段雷达数据处理系统的设计原则。蒙特卡洛仿真实验的结果与理论分析结果高度吻合,因而本文根据理论分析设计的数据处理系统是有效的。

[1]郦晓翔.雷达反隐身技术的发展及实现方法[J].电子工程师,2008,34(8)：3-5,34.

[2]SKOLNIK M I.雷达系统导论[M].左群声,徐国良,马林,译.北京：电子工业出版社,2007：177-178.

[3]BRENNER T,KUSCHEL H,OLSEN K E.Multiband Radar Modelling[C]//International Radar Symposium,Krakow,Poland：[s.n.],2006：1-7.

[4]张峰.空馈双面阵相控阵雷达工作方式设计及特点[J].现代雷达,2007,29(7)：31-33.

[5]吴永亮.美国海军舰载双波段系列雷达的发展[J].国防科技,2012,33(4)：14-20,31.

[6]袁桂生.双面阵三坐标雷达数据处理算法研究[J].雷达与对抗,2000(4)：60-64.

[7]潘宁,张林让.主被动雷达数据融合及跟踪[J].雷达科学与技术,2008,6(1)：61-64.PAN Ning,ZHANG Lin-rang.Angle Fusion and Tracking of Active and Passive Radars[J].Radar Science and Technology,2008,6(1)：61-64.(in Chinese)

[8]杨科技,郑成波,傅其祥,等.一种雷达组网融合实时处理系统设计与实现[J].电子设计工程,2011,19(18)：130-133.

[9]郭明,许录平.集中式多雷达系统的数据融合[J].雷达与对抗,2003(1)：19-22.

[10]吴顺君,梅晓春.雷达信号处理和数据处理技术[M].北京：电子工业出版社,2008：516-517.

[11]石章松,刘忠,王航宇,等.目标跟踪与数据融合理论及方法[M].北京：国防工业出版社,2010：271-272.

[12]韩伟,黄晓斌,张亚标.两面阵双波段雷达的跟踪滤波性能分析[J].雷达科学与技术,2011,9(1)：58-61.HAN Wei,HUANG Xiao-bin,ZHANG Ya-biao.Analysis of Tracking Filter Performance of Two-Face Array Dual-Band Radar[J].Radar Science and Technology,2011,9(1)：58-61.(in Chinese)

[13]黄晓斌,张燕,韩伟.双面阵雷达目标跟踪性能分析[J].空军雷达学院学报,2011,25(1)：12-14,24.