基于SVDD的中段目标综合识别分类器设计

(国防科技大学电子科学与工程学院,湖南长沙410073)

0 引言

目标识别是弹道导弹防御系统实现作战功能的重要保证,是保证从预警跟踪阶段到拦截器寻的阶段都能实现有效跟踪和拦截的关键支撑技术之一。从20世纪60年代开始,不论导弹防御研究的热点怎样调整,目标识别技术一直是其核心问题之一[1]。国内外投入了大量的人力物力研究相关识别算法。为了提高识别器的分类性能,越来越多研究者开始致力于多特征综合识别的研究。

由于诱饵能够模拟真实目标一种或者几种特征,但是做不到模拟真实目标全部特征。综合利用传感器的多层次融合可以有效提高识别的正确率、抗干扰性能,并扩展识别的范围[2]。弹道导弹中段识别面临的目标群环境很复杂,包括弹头、重诱饵、发动机碎片、弹体碎片等,对于弹头目标由于其形状简单,其特性与数据相对容易预测和获得,而对于轻/重诱饵、碎片等其他干扰目标,由于弹头弹体分离后弹体爆炸产生碎片的随机性与运动复杂性,很多时候难以准确完整地进行描述。因此,研究在目标群先验信息稀缺的模式下的目标综合识别方法极具实际意义。

随着现代模式识别技术的发展,越来越多的分类算法被应用于雷达综合目标识别中,如贝叶斯分类器、k均值分类器、神经网络分类器、支持向量机分类器、模糊函数分类器等。弹道目标识别是典型的非合作目标识别,突防目标特性是进攻方的军事机密,目标识别传感器(主要是雷达)不仅难以获得待识别目标群的特征数据库,甚至连真假目标类型和数目都知之不详,因此上述识别方法存在种种限制而难以直接应用[3]。

支持向量数据描述(SVDD,support vector data description)[4],是一种单值分类器或奇异点检测器。其特点在于可以不需要非目标类的先验训练样本,适用于非弹头类目标群先验信息难以描述的中段弹道目标识别场景。为了更好地解决在该场景模式下的识别问题,本文深入研究了SVDD方法在目标综合识别中的应用,引入模糊隶属度的概念,设计了基于SVDD的单类目标筛选分类器、多类目标分类器,并给出该方法的综合识别流程。分别基于仿真数据、暗室数据、测量数据验证了方法的有效性。

1 核函数和SVDD

1.1 核函数

核方法主要是利用核函数将原数据空间中的非线性问题转化为特征空间中的线性运算,以避免复杂的高维计算,同时实际运算中也不需要知道非线性映射的具体形式。

设x和x′为数据空间中的样本点,数据空间到特征空间的映射函数为Φ(·),核方法的基础是实现向量的内积变换,

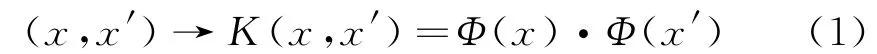
通常,非线性变换函数Φ(·)相当复杂,而运算过程当中实际用到的核函数K(·,·)则相对简单。

核函数必须满足Mercer条件[5]。目前,应用较多的几种核函数如下：

(1)径向基核函数(RBF)

(2)q次多项式核函数

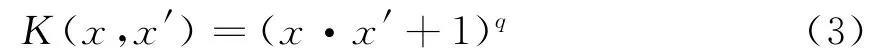
(3)Sigmoid函数(或两层神经网络)

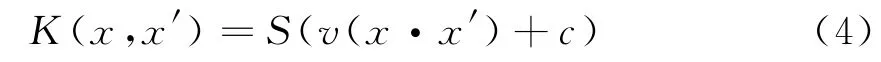
(4)小波核函数

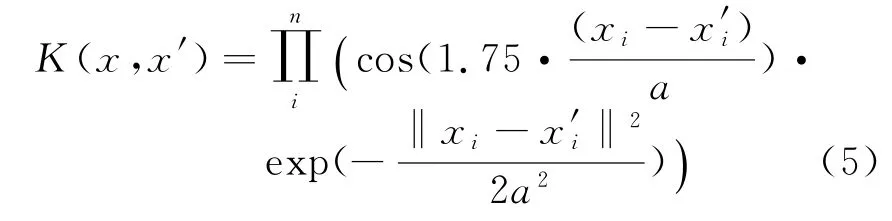
上面四个公式中a,q,v,c都是常数,S(·)是Sigmoid函数。本文中采用应用最为广泛的RBF核函数。

1.2 SVDD方法

SVDD的基本思想是在经过核映射的高维空间里构造一个包含目标训练样本的最小超球半径球体,用这个球体准确地描述数据,对于落入超球外的测试数据均被认为是非目标类[6]。

设目标类样本集合为X={X1,X2,…,X N},首先通过非线性映射将样本映射到高维空间,再在高维空间进行支持矢量数据描述。样本由原空间X映射到高维特征空间Φ(X),映射后特征空间的样本集合变为

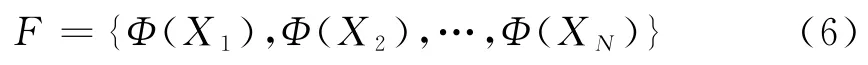
考虑部分样本落入球外的一般情况,为了减少这些点的影响,引入松弛变量ξi(ξi≥0),C表示惩罚因子,用以控制超球半径与样本点落入球外数目之间的折衷,r为包含所有样本的最小超球半径,a为超球球心。

则优化目标函数为

约束条件为

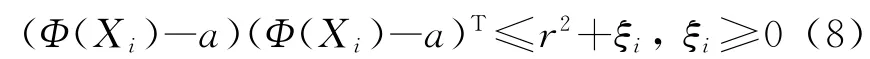
上式为一个二次规划问题。由式(7)和式(8)可以构造如下的Lagrange函数：

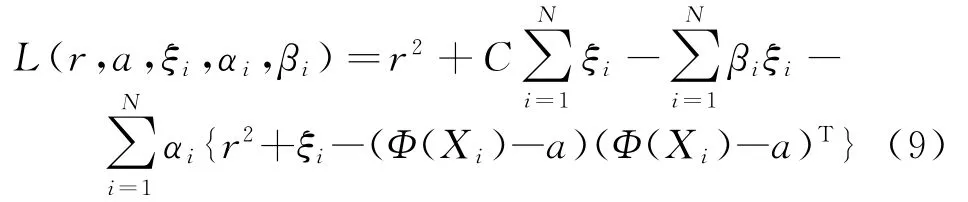
式中,αi≥0,βi≥0,为Lagrange乘子,求上式对a,r,ξi偏微分得

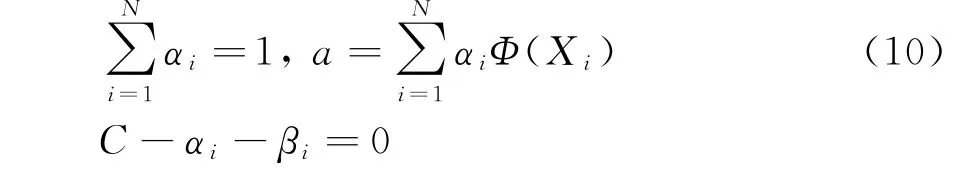
由于Lagrange乘子αi,βi都大于零,去掉βi,用C≥αi≥0进行限制,代入L(r,a,ξi,αi,βi),推导整理得

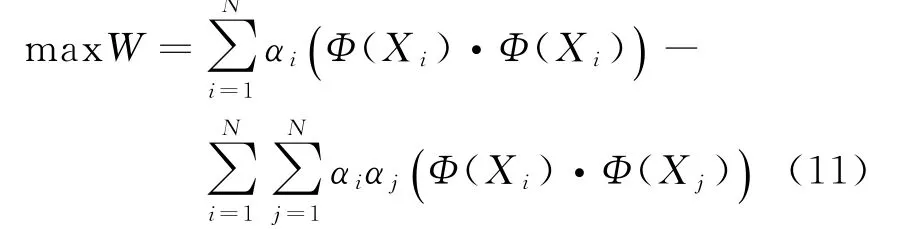
约束条件为

解该优化问题可得到αi的值,通常情况下大部分αi为0,只有部分αi满足C≥αi＞0,它们对应的样本即支持矢量,由它们来确定超球半径R2。R2为边界上任意一个支持矢量到球心a的距离的平方,又K(X i,X j)=Φ(X i)·Φ(X j),则超球半径为

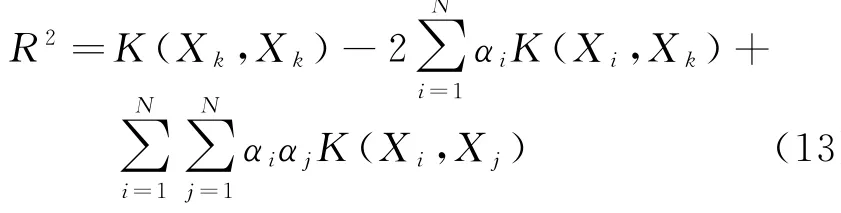
式中,X k∈SV,SV为支持向量集,对应于C≥αi＞0。对于测试样本z,映射后为Φ(z),特征空间中测试样本到球心a距离为

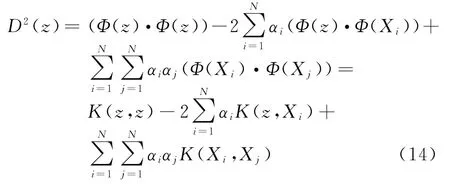
通过测试样本到球心距离与训练得到的超球半径比较,可实现测试样本的分类,即

2 基于SVDD的分类器设计

2.1 单类目标筛选方法

SVDD方法根据目标类信息构造最小超球来区分目标类和非目标类,也就意味着在中段目标综合识别中,只需要获得弹头目标先验数据并对其训练,通过核映射在特征空间中构造弹头的最小超球分类边界,基于此超球边界就可以实现该背景下的目标分类,从而能较好地避免了先验信息不足的情况下采集和获取诱饵、碎片先验数据时存在的巨大困难。

由于非目标类数量可能较多,识别是个不断筛选威胁程度高的目标的过程,故此种非“是”即“非”的硬判决在多个目标的二分类判决中并不十分适用。文章引入模糊集理论中模糊隶属度的概念,将判决部分根据隶属度的大小输出目标威胁程度排序。测试样本越靠近目标超球球心则属于目标类的可能性越大,反之则越小,故假设同一时刻待识别的威胁样本个数为K,z k(k∈K)属于目标类的模糊隶属度函数m(z k),m(z k)的表达式如下：

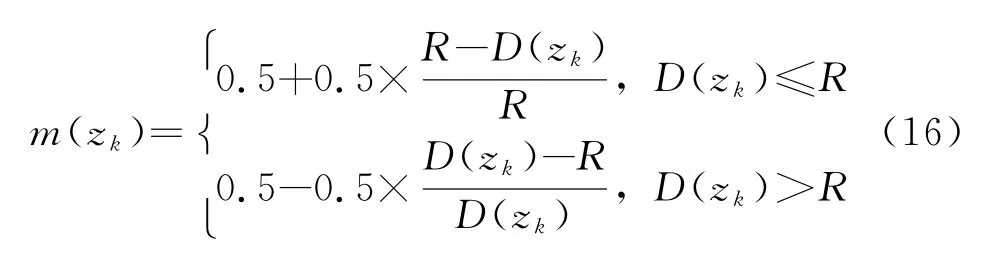
模糊隶属度的引入使得每个测试样本的输出值为目标为弹头的可能性,同一时刻多个目标则可根据m(z k)值大小进行威胁排序,取值最大或靠前者对应的样本判为目标类,即目标样本为

由上述理论可知,超球半径R的描述对于分类性能尤为重要。在实际应用中,要根据识别需求,在RBF的条件下,通过训练求出σ和C的最佳组合,从而求得最佳超球半径R。在训练参数先验知识库中应该储备根据不同情况特征数据描述对应的最佳参数集信息,为测试识别提供自适应选择的最优参数。

设训练样本数中,目标类样本数为P,非目标类样本数为Q,当目标类样本判为目标类的次数为TP,非目标类判为目标类的次数为FP,则对应的概率分别为实警概率P TP=TP/P、虚警概率P FP=FP/Q,根据ROC曲线关系,采用w=作为最优超球半径的选取准则函数[7]。当w值最大时所对应的即为C和σ的最佳组合,相应的半径值即为最优超球半径,此时目标有较高的实警概率,同时对虚警概率的兼顾性也较好。

2.2 多类目标分类方法

若目标群可获取的先验信息较为丰富,对威胁目标类特征描述不仅止于目标弹头类,还可获得其他部分类别目标的信息,则可以扩展到SVDD方法在多目标的识别中的应用。若训练样本为不限于目标类样本的多类样本,经典的多分类方法思想如图1所示,设共有M类目标样本,n∈M,分别对每一类训练样本描述球心a n以及测试样本到球心距离d n,找出最小d n,则测试样本属于对应的第n类,即

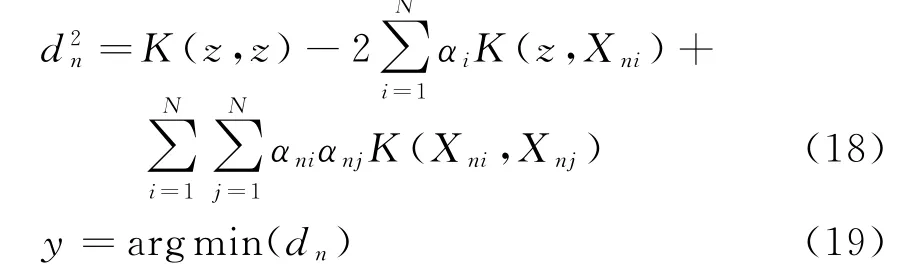
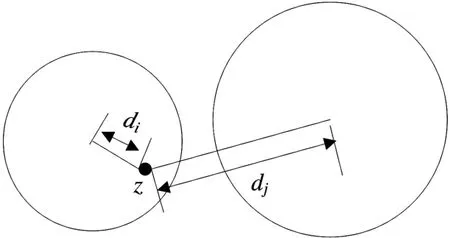
图1 经典的多分类思想示意图(二分类为例)

经典方法物理意义明确,步骤简单,但在中段目标识别中应用存在两个问题。首先,在先验信息不能将威胁目标群所有类别都进行描述的情况下,即训练样本不全面的情况下,经典方法只在有训练样本的目标类别间进行判别,未考虑到其他目标类型的存在;第二,经典方法的实质为利用RBF核函数将训练样本由原空间映射到特征空间,并且根据惩罚因子C描述各已知类别样本的最小覆盖超球,再根据待测样本到各类超球球心距离判断类别。但是对应不同超球,d n的大小关系与类别的从属没有固定的关系,经典方法的判别在某些情况下不适用,例如：情况一如图2(a)所示,d j＜d i应判别目标为j类,但实际上目标为i类;情况二如图2(b)所示,d j=d i则目标判为i类或j类的概率相等,但实际上目标为i类的可能性更大;因此仅根据d n进行判别并非完全准确的稳定判据,必须考虑各超球的特性进行判别。

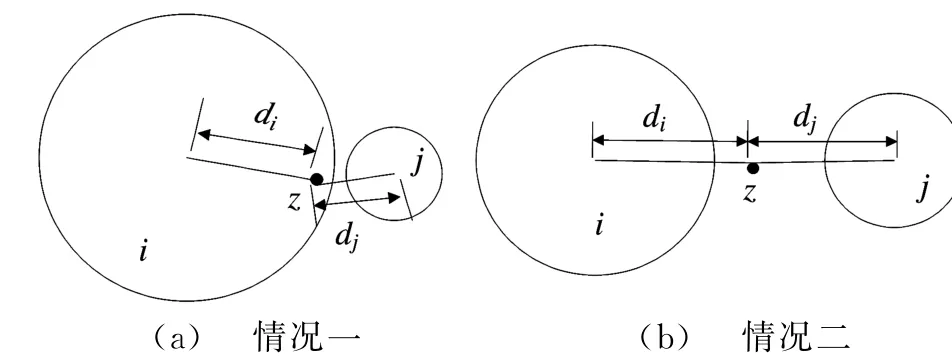
图2 经典多分类SVDD不适用的情况

基于对上述问题的考虑,类似上节单目标筛选方法,本文通过模糊隶属度的引入来解决上述问题。参考文献[8]中SVDD模糊描述的思想,设共有M类目标样本,n∈M,分别对每一类训练样本描述最小超球半径R n以及测试样本到球心距离d n,目标样本z属于第n类的模糊隶属度函数m n(z)。隶属度应该基于R n与d n的关系给定,观测样本同时在两个超球内时,距离球心越近则隶属度越大;观测样本同时在两超球外时,则可以同时考虑距球面的距离来定义隶属度。则m n(z)可定义为

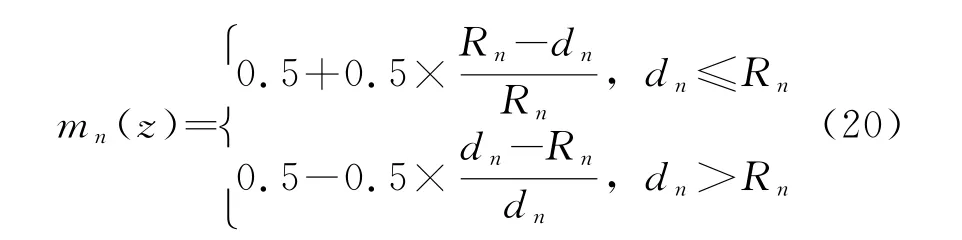
根据测试样本对于各类别隶属度m n(z)值的大小,判定为对应m n(z)值最大的类别为目标类别。当测试样本距离两超球面距离均较大,m n(z)值则十分小,则为其他类别样本的可能性很大。根据先验知识及训练情况设定阈值δ,使隶属度在该阈值以下时判为其他类,对应可以解决第一个问题。故测试样本z的类别为

隶属度的模糊描述中利用了各类超球自身超球半径的信息,故生成隶属度的比较比单纯根据距离大小判别更准确,对应可以解决第二个问题。

2.3 基于SVDD的分类器识别流程

非合作的中段目标群识别对于威胁目标的先验信息难以获取,给传统识别方法带来很大困难。SVDD的通过寻找最小超球面来筛选目标类的思想为解决这个问题提供方法。本文引入模糊隶属度,设计了基于SVDD的分类器,根据前述内容给出识别流程图,如图3所示。

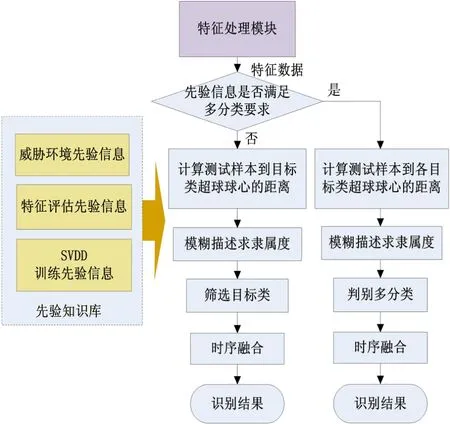
图3 基于SVDD的分类器识别流程图

根据威胁环境先验信息及特征评估先验知识,对待识别场景进行一定预测与描述,并将此信息通过训练得到目标最小超球描述信息。结合当前时刻特征数据的分析结果,判断需要进行单类目标的筛选还是多目标的分类。若只具备弹头类目标的先验信息,则按照2.1节描述的单类目标筛选方法筛选出目标类;若具备不止弹头类的其他弹体或诱饵具体先验信息,则按照2.2节描述的多类目标分类方法进行多类的判别。得到当前时刻的分类结果信息后,经过时序融合可得到最后的识别结果。

3 仿真实验与分析

3.1 仿真数据实验

下面用生成的仿真特征数据对基于SVDD的分类器进行实验。选取具明确物理意义又兼较好可分性的目标特征：RCS均值、RCS方差、散射点个数、微动周期。假设雷达从100 s开始观测数据,共获取500 s的观测数据,特征提取统计窗长度为10 s,滑动窗长为5 s。根据先验知识及相关资料,观测特征数据由一组设定的真值加入一定相对值的随机误差来模拟,如假设四类目标的微动周期分别为5 s,4 s,3 s,0,加上随机生成的一定范围内的误差值以模仿测量及其他原因带来的数据误差,得到用于验证分类有效性的观测特征数据。最终得到的仿真目标群特征数据如图4所示。

图4 仿真数据目标群特征

实验单类目标筛选方法时,假设仅已知弹头的先验信息即仅有弹头训练数据,再对测试样本进行分类;实验多类目标分类方法时,则假设部分目标先验信息未知,再对测试样本进行分类。由于时序融合方法非本文研究重点,故本节仿真实验中不作具体实现要求。

首先,实验单类目标筛选方法。在RBF的条件下,取训练数据样本200组,根据训练样本求出最优参数σ和C。设定参数变化范围,求出每组参数的目标识别率(P TP)及非目标识别率(1-P FP),如图5所示。由图可以看出RBF参数σ的变化对目标识别率及非目标识别率的影响较小。目标识别率随着惩罚因子C的增大而逐渐递增,而非目标识别率随着惩罚因子C的增大而逐渐递减,故需要合理权衡。按照2.1节所述,令最大,求出对应的C和σ即为最佳组合,进一步求出最优超球半径。在上述条件下,求得C=0.16,σ=2.0,R=0.582 2。

根据得到的训练参数,生成800组测试样本进行分类,得到的识别结果如表1所示,识别率为将列标题对应类别识别为行标题类别的概率。

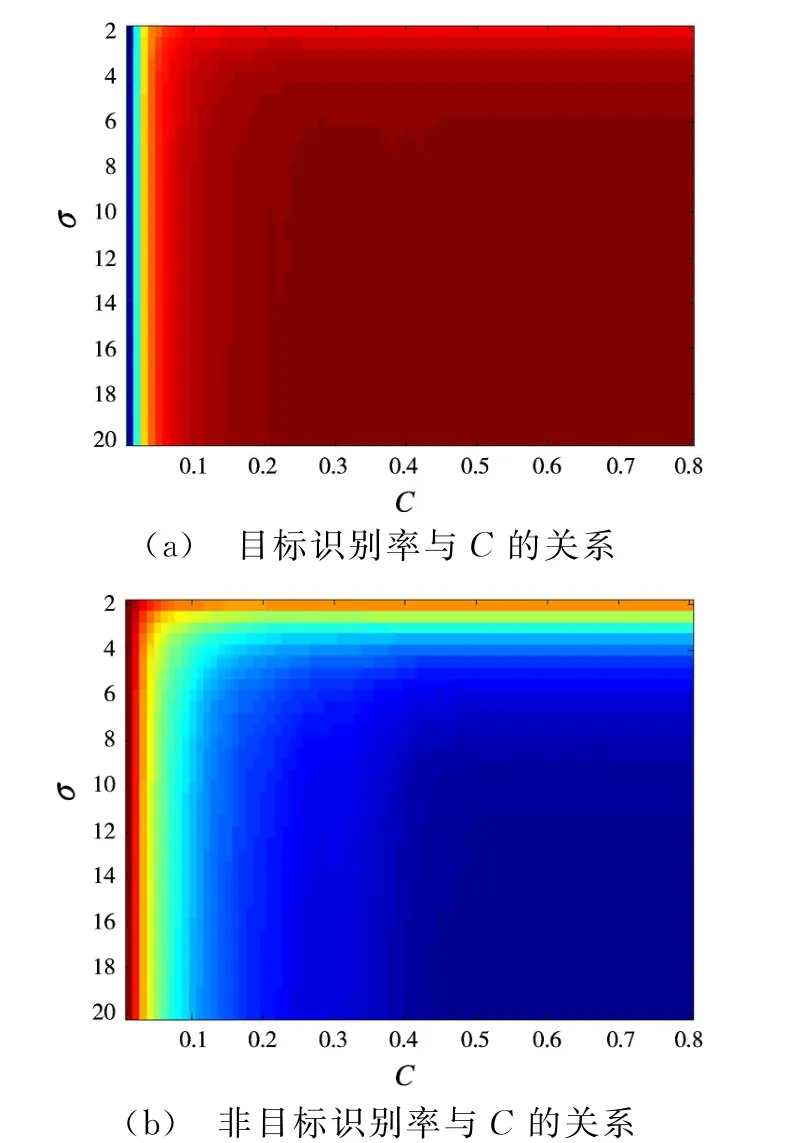
图5 识别率随参数σ、C变化图

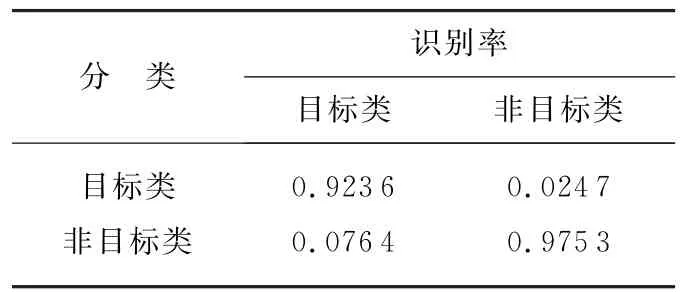
表1 单目标筛选分类结果

由上表可以看出,在仅有目标类先验信息时,单目标筛选方法的识别性能较好。把非目标类误判为目标类的概率小于把目标类误判为非目标类的概率,即虚警概率大于漏警概率。

下面,对多类目标分类方法进行实验。实验中将未知先验信息的目标类判为其他类。

(1)已知弹头类和其他任意一类诱饵先验信息

分别假设已知弹头类和另外某一类诱饵类先验信息,分别对相应描述的200组数据进行训练,选择最优参数。生成800组测试样本进行分类,分别得到的识别结果如表2、表3和表4所示。

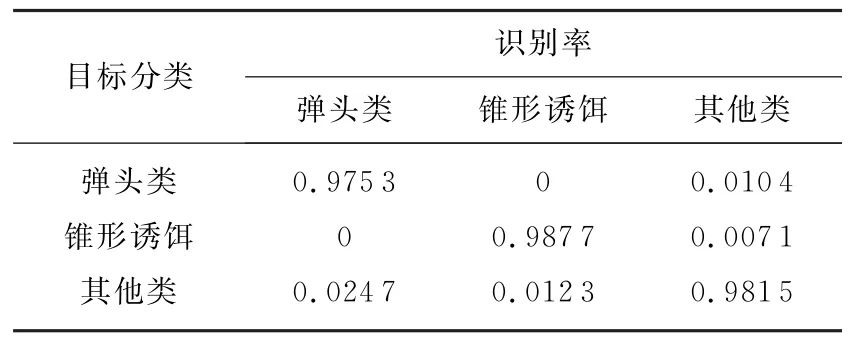
表2 已知弹头、锥形诱饵先验信息多目标分类结果

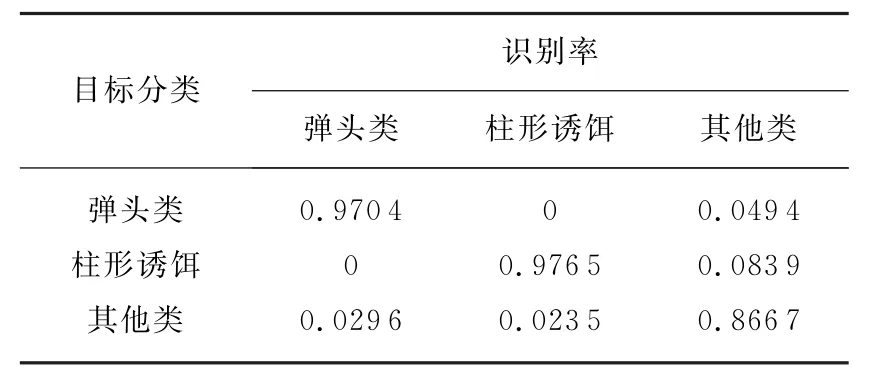
表3 已知弹头、柱形诱饵先验信息多目标分类结果

表4 已知弹头、球形诱饵先验信息多目标分类结果

由上表结果可以看出,已知弹头类及任意一类诱饵先验信息的情况下,利用基于SVDD的多类目标分类方法分类效果较好。对已知先验信息的两类识别率相对其他类更高。相比单类目标筛选方法,弹头类的识别率更高,可见更多的先验信息对提高弹头类识别率有帮助。

(2)已知弹头类和其他任意二类诱饵先验信息

分别假设已知弹头类和其他任意两类诱饵类先验信息,分别对相应描述的200组数据进行训练,选择最优参数。生成800组测试样本进行分类,分别得到的识别结果如表5、表6和表7所示。

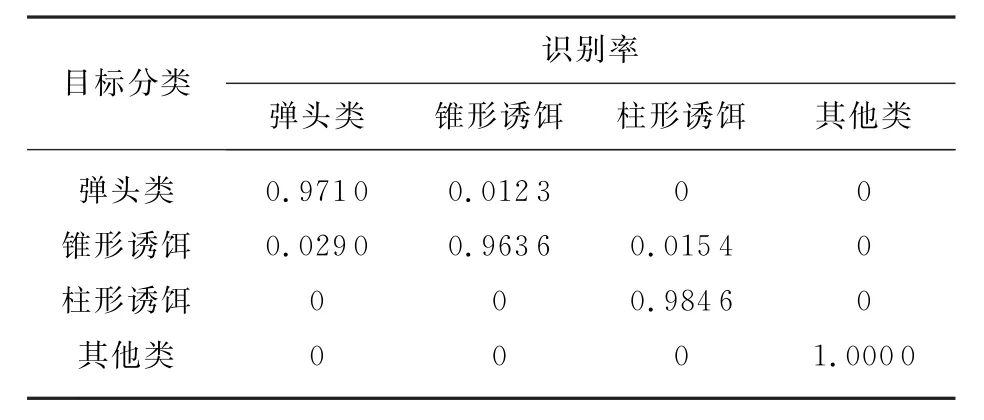
表5 已知弹头、锥形、柱形诱饵先验信息多目标分类结果

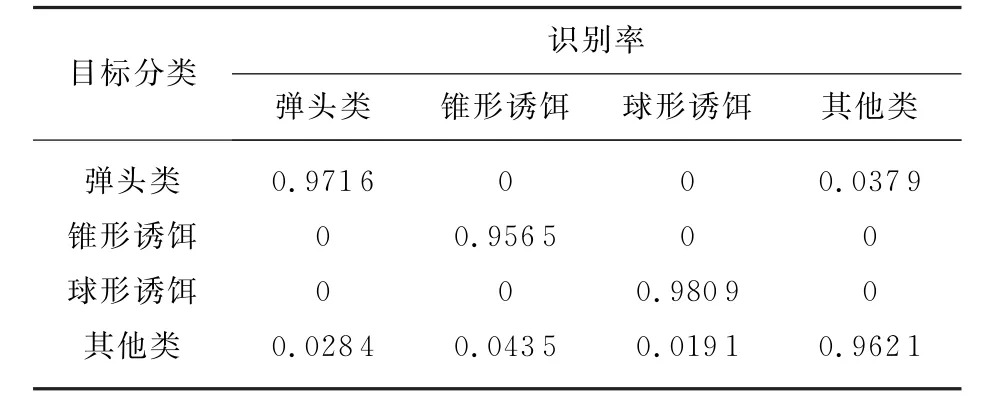
表6 已知弹头、锥形、球形诱饵先验信息多目标分类结果

表7 已知弹头、球形、柱形诱饵先验信息多目标分类结果

由上表结果可知,在已知弹头类和其他两类诱饵先验信息的情况下,利用基于SVDD的多类目标分类方法分类效果较好。

(3)已知全部目标类先验信息

假设已知目标群类别全部先验信息,分别采用经典的SVDD多分类方法和本章SVDD多分类方法对仿真数据测试样本进行分类,得到的识别结果如表8所示。

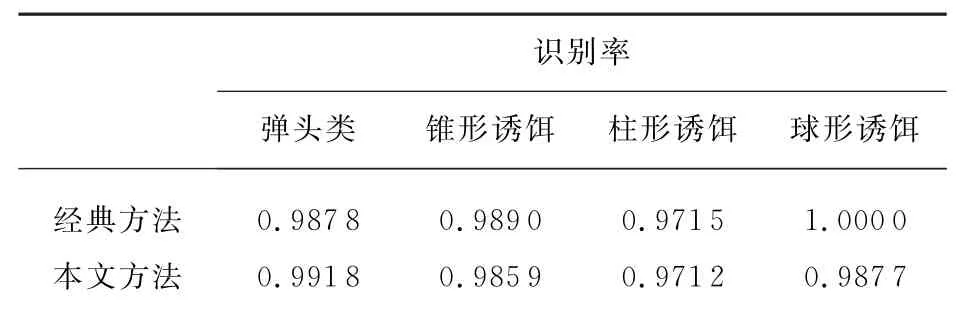
表8 已知全部目标类先验信息多目标分类结果

由上表结果可知,在全部先验信息已知的情况下,采用SVDD经典多分类方法和本章多分类方法的识别性能均较好。先验信息丰富的条件下,比上述几种先验信息不完整条件下的识别性能更高。可见对威胁目标的识别,先验信息库的构建至关重要。

3.2 暗室数据实验

接下来用暗室数据验证本文方法的有效性。威胁场景设置：一个弹头、一个助推器(柱形诱饵)、一个锥形诱饵、一个球形诱饵。由弹道方程仿真计算得到弹道数据,根据目标的弹道序列,计算相应时刻目标相对于雷达观测视线的姿态角,通过拟合合成宽/窄带雷达回波数据,并通过特征提取算法提取目标特征。

按时序对100个观测单元提取的目标特征,包括RCS均值、RCS方差、散射点个数、微动周期,如图6所示。

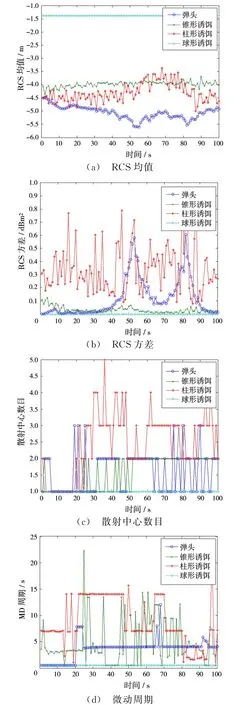
图6 暗室数据目标群特征

将数据分为两组：训练组和测试组。首先,验证单类目标筛选方法。假设仅已知弹头组的先验信息即仅用弹头组训练数据进行训练,选择最优参数。再对测试组样本进行分类。得到的结果如表9所示。

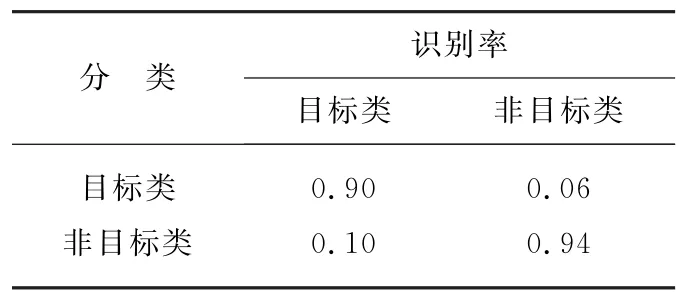
表9 单目标筛选分类结果

由上表可以看出,仅有弹头先验数据的情况下,SVDD单目标筛选分类识别率较好,比仿真数据效果稍差。

下面与上节基于仿真数据实验的步骤一致,对多类目标分类方法进行验证。将未知先验信息的目标类判为其他类。

(1)已知弹头类和其他任意一类诱饵先验信息

分别假设已知弹头类、锥形诱饵类,弹头类、柱形诱饵类,弹头类、球型诱饵类信息,并分别对相应训练组数据进行训练,选择最优参数。对测试组进行测试分别得到的识别结果如表10、表11和表12所示。

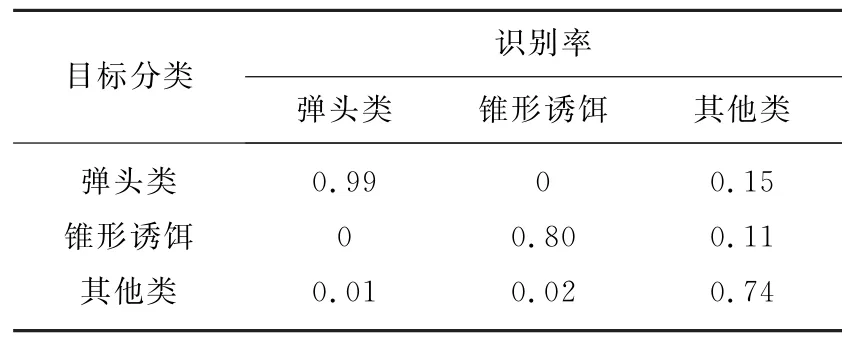
表10 已知弹头、锥形诱饵先验信息多目标分类结果

表11 已知弹头、柱形诱饵先验信息多目标分类结果

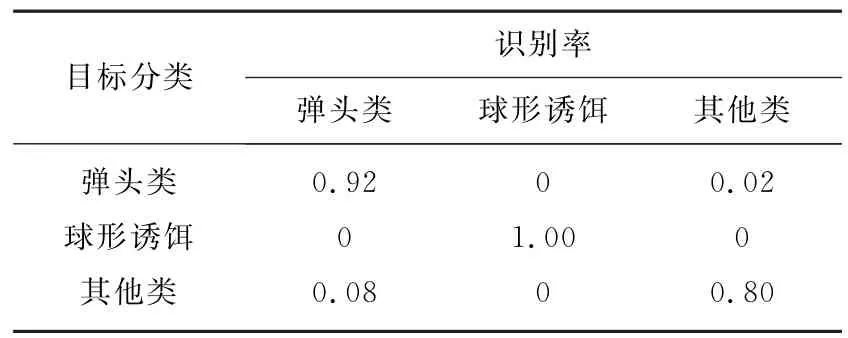
表12 已知弹头、球形诱饵先验信息多目标分类结果

由上表结果可以看出,已知弹头类及任意一类诱饵先验信息的情况下,利用基于SVDD的多类目标分类方法结果稍逊于基于仿真数据的结果,可能是由于暗室数据的不稳定性造成。对弹头类的识别率在0.85以上。由于先验信息不足,其他类易误判为已知两类目标,故识别概率低于已知先验信息的两类。

(2)已知弹头类和其他任意二类诱饵先验信息

针对假设已知弹头类和其他任意两类诱饵先验信息的情况分别进行训练,选择最优参数。对测试组样本进行分类,得到的识别结果如表13、表14和表15所示。

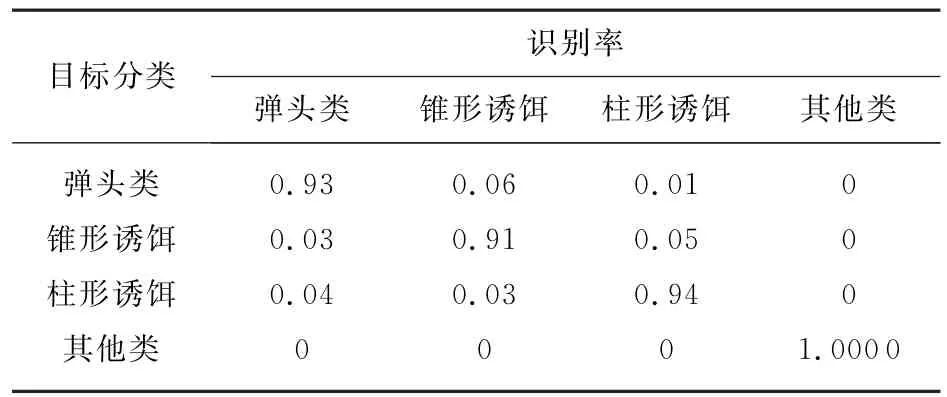
表13 已知弹头、锥形、柱形诱饵先验信息多目标分类结果

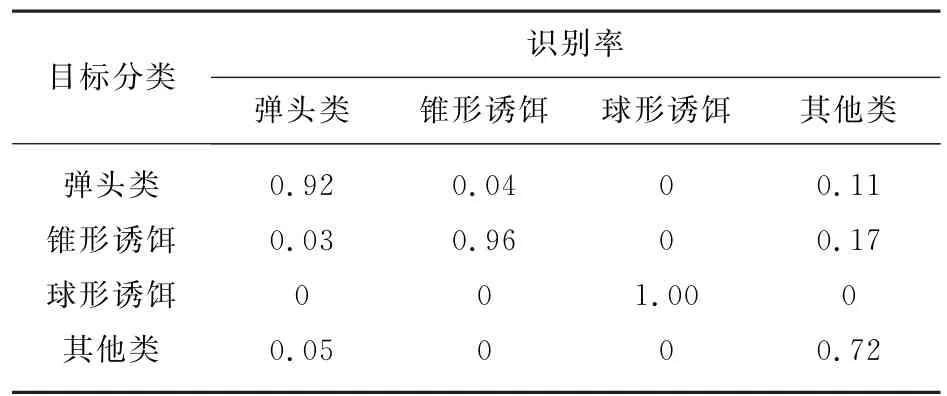
表14 已知弹头、锥形、球形诱饵先验信息多目标分类结果

表15 已知弹头、球形、柱形诱饵先验信息多目标分类结果

由上表结果可知,在已知弹头类和其他两类诱饵先验信息的情况下,利用基于SVDD的多类目标分类方法,对弹头类的识别率在0.9以上。由于球型诱饵特征区分度较大,所以在各情况下对其识别概率均较高。当锥形诱饵或柱形诱饵先验信息未知时,易引起其他类的误判。

(3)已知全部目标类先验信息

假设已知目标群类别全部先验信息,分别采用经典的SVDD多分类方法和本文SVDD多分类方法对暗室数据测试样本进行分类,得到识别结果如表16所示。

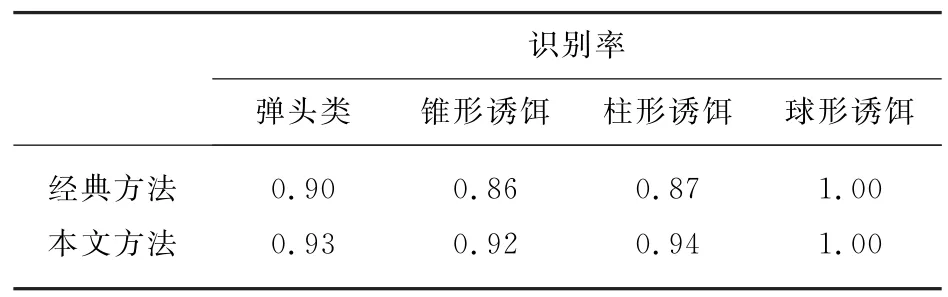
表16 已知全部目标类先验信息多目标分类结果

由上表结果可知,在全部先验信息已知的情况下,采用SVDD经典多分类方法和本文多分类方法对弹头的识别性能均较好,后者对锥形诱饵柱形诱饵的识别效果更好。和基于仿真数据的结果一样,先验信息丰富的条件下,比上述几种先验信息不完整条件下的识别情况要更好。

4 识别评估

弹道目标识别系统是典型的多目标、多特征、多传感器融合识别系统,识别手段的多样性也给系统的综合集成带来了一定的难度,对识别进行可靠性评估变得十分必要[9]。本文采用基于置信度估计的方法对识别结果进行评估。

所谓置信度是对正确概率的一种度量,是表示某一事件可靠程度的一种指标。在目标识别中,置信度定义为一个用来衡量模型和观测数据之间匹配程度的函数,而且该函数值对于不同观测数据具有可比性。

针对本文仿真实验,我们分别用已知弹头信息、已知弹头和一类诱饵信息、已知弹头和两类信息以及已知全部信息四种识别类型,对识别结果进行评估。隶属度判决门限均取为0.5,在相同条件下进行连续多次的仿真,总共获得5 000组目标特征数据,其中包括所设置的真目标2 400组,诱饵2 600组。得到的结果如表17所示。

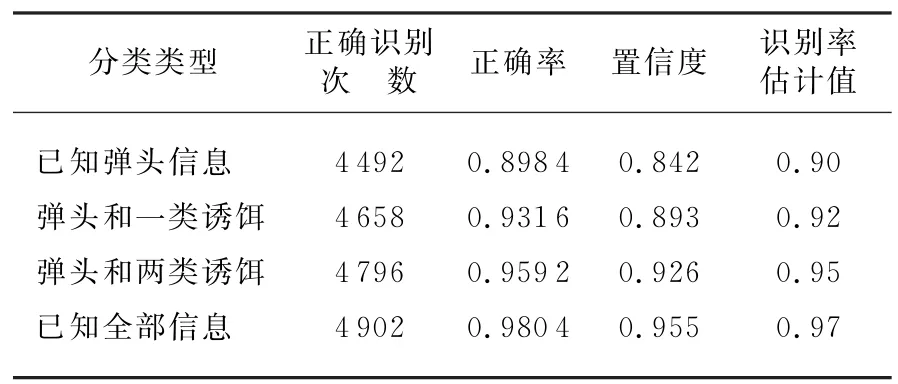
表17 识别结果及评估结果

根据表17可以看出,已知的先验信息越多,分类器的性能越好,置信度也越高。只有弹头信息时,虽然对先验信息的要求最低,但是分类器判决时出现错误判决的概率最大,得到的识别率和置信度都较低;而已知全部信息时,分类器判决错误的概率最低,得出的识别结果是最好的。所以,在进行分类识别时,尽可能地知道所有先验信息,是提高识别性能的最主要手段之一。

5 结束语

针对特定场景的高效、稳健的分类算法,对真假弹道目标识别乃至国家反导防御系统的建设具有重要意义。已有的识别方法大多依赖全面的先验数据库支持而使得其实用性受限。本文根据弹道目标识别先验信息有限且非目标类先验信息难以获取和描述等特点,研究了SVDD方法在弹道目标综合识别中的应用,设计了基于SVDD的弹道目标分类器,并给出识别流程。根据获取先验信息量的多少,分别采用单类目标筛选方法及多类目标分类方法,在经典的SVDD方法上引入模糊隶属度的概念,使得功能上更能满足反导场景的需要。仿真结果验证了该方法在上述场景下的识别有效性。另外,更完善的识别评估反馈、先验信息的更深入应用将能进一步提高分类性能及实际可用性。

[1]张光义.空间探测相控阵雷达[M].北京：科学出版社,2001.

[2]马梁.弹道中段目标微动特性及综合识别方法[D].长沙：国防科技大学,2011：90-91.

[3]冯德军,丹梅,来庆福,等.模糊分类树在弹道目标识别中的应用[J].导弹与航天运载技术,2010(5)：30-33.

[4]BANERJEE A,BURLINA P,DIEHL C.A Support Vector Method for Anomaly Detection in Hyperspectral Imagery[J].IEEE Trans on Geoscience and Remote Sensing,2006,44(8)：2282-2291.

[5]陈长军.基于SVDD与SVM的人脸识别技术应用研究[D].镇江：江苏大学,2009.

[6]TAO X M,CHEN W H,DU B X,et al.A Novel Model of One Class Bearing Fault Detection Using SVDD and Genetic Algorithm[C]//2nd IEEE Conference on Industrial Electronics and Appli-cations,Harbin,China：[s.n.],2007：802-807.

[7]万柏坤,薛召军,李佳,等.应用ROC曲线优选模式分类算法[J].自然科学发展,2006,16(11)：1511-1516.

[8]郭雷,肖怀铁,付强.一种新的支持矢量数据描述模糊识别方法[J].系统仿真学报,2009,21(7)：1882-1886.

[9]王欢,何明浩,刘锐,等.雷达信号识别效果的模糊综合评价研究[J].雷达科学与技术,2012,10(4)：372-375.WANG Huan,HE Ming-hao,LIU Rui,et al.Research on Fuzzy Comprehensive Evaluation of Radar Signal Recognition Effect[J].Radar Science and Technology,2012,10(4)：372-375.(in Chinese)