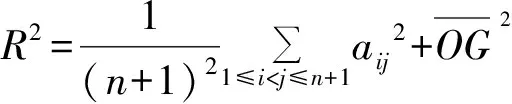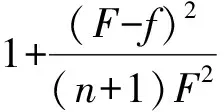En中n维Euler不等式的再改进
陈士龙
(安徽广播影视职业技术学院,安徽 合肥 230011)
0 引言
先简单回顾n维Euler不等式研究的大致过程。
在二维平面上,对于任意三角形,其外接圆半径与内切圆半径间存在如下的不等式关系:
R≥2r
(1)
当且仅当三角形为正三角形时,式(1)等号成立。
文献[1]中将式(1)推广到n维欧氏空间,建立了n维Euler不等式:
R≥nr
(2)
当且仅当单形σn为正则单形时,式(2)等号成立。
1985年,M.S.Klamkin[2]推广了式(2),得到下面的不等式:
(3)
当且仅当单形σn为正则单形时,式(3)等号成立。
关于n维Euler不等式,文献[3]给出了2种情况的推广:
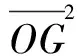
(4)

当且仅当单形σn为正则单形时,式(4)、式(5)等号成立。
设θ为单形σn的所有对棱所成角的算术平均值,冷岗松[4]对n维Euler不等式作了新的加强:
R2≥cscθ·n2r2
(6)
当且仅当单形σn为正则单形时,式(6)等号成立。
文献[5]对式(2)作了进一步的推广,得到下面的一些结果:
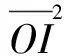
(7)
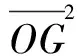
(8)

当且仅当单形σn为正则单形时,式(7)、(8)、(9)中等号成立。
本文将n维Euler不等式作了新的加强,得到了下面新的几何不等式。
定理1 记F=max{Fi},f=min{Fi}(i=1,2,…,n+1 ),即F与f分别表示单形σn的各侧面面积的最大值和最小值,对En中n维单形σn,下列不等式成立:
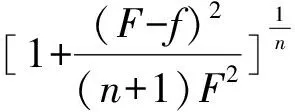
(10)
当且仅当单形σn为正则单形时,式(10)等号成立。
1 引理
引理1[6]对En中n维单形σn,下列等式成立:
(11)
当且仅当单形σn为正则单形时,式(11)等号成立。
引理2[7]对n维欧氏空间En中n维单形Ωn,顶点为A1,A2,…,An+1,体积为V,任取k+1个顶点所支撑的k维单形的k维体积为Vi0i1…ik(0≤i0 (12) 引理3[8]对En中n维单形σn,下列不等式成立: (13) 当且仅当单形σn为正则单形时,式(13)等号成立。 由幂平均不等式得: (14) 由算术-几何平均不等式得: (15) 由式(12)和式(15)得: (16) 结合式(16)和式(13),可得: (17) 由式(17)和式(11)得: (18) (18)式即为定理1。由证明过程可知,当且仅当单形σn为正则单形时,定理1中等号成立。 参考文献 [1] Klamkin M S,Tsintsifas G A.The circumradius-inradius inequality for a simplex[J].Math Magazine,1979,52(1):20-22. [2] K lamkin M S.Inequality for a simlex[J].SIAM Rev.,1986,28(4):579-580. [3] Shiguo Y,Jia W.Improvements of n-dimensional Euler inequality[J].Jornal of Gomry,1994,51(1-2):190-195. [4] 冷岗松.En中Euler不等式的一个加强[J].数学的实践与认识,1995(2):94-96. [5] 杨世国.关于n维Euler不等式的一些推广[J].四川大学学报(自然科学版),2003,40(5):802-805. [6] 沈文选.单形论导引[M].长沙:湖南师范大学出版社,2000:111-112. [7] 王文,杨世国.欧氏空间En中Pedoe不等式的推广[J].中国科学技术大学学报,2012,42(11):913-919. [8] 陈士龙,杨世国.En中Gerber不等式的加强与应用[J].淮北煤炭师范学院学报(自然科学版),2007,28(1):6-9.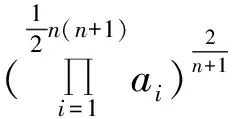
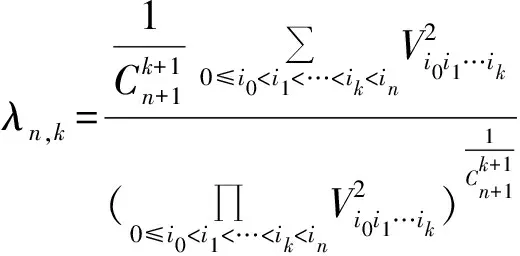
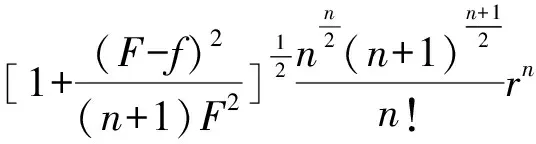
2 定理的证明: