基于SVM线性核函数情感分类模型的建立和研究*

戴晓娟

(宁夏师范学院)

0 引言

音乐是一种借助乐和音来表现情感的艺术，通过不同的元素、巧妙的组合展现给我们一个丰富的情感世界.随着时代的发展，人们逐渐将计算机技术应用到音乐领域，将音乐数字化、生活化，极大丰富了音乐的表现力和感染力.

流行音乐的主要传播媒介从传统的电台和唱片逐渐渗入到网络下载和网络电台等.网络电台需要结合收听者的喜好，自动推荐并播放其他音乐.由于每个人喜好的音乐可能横跨若干种风格，区别甚大，需要分别对待.在流行音乐中，传统的风格概念包括Pop(流行)、Country(乡村)、Jazz(爵士)、Rock(摇滚)、R＆B(节奏布鲁斯)、New Age(新世纪)等若干大类，它们分别又可以细分成许多小类，有些小类甚至可以做更进一步的细分.而每首歌曲只能靠人工赋予风格标签.但这样的做法有许多不足:有的类别之间关系不清楚，造成混乱;有的类别过度粗略或精细;有的类别标签没有得到公认;有的音乐归属则存在争议或者难以划归.没有一个统一的标准，因而就需要探讨如何区分音乐风格.

针对流行音乐分类方法存在的问题，提出一种基于多分类SVM的流行音乐情感分类的研究.将线性方法和“一对多”方法结合起来.在所构建的情感音乐模型中，将音乐所表达的情感分为四类，分别是“单身的”、“沧桑的”、“媚惑的”、“迷茫的”.

1 问题的提出

(1)SVM和线型核函数能将流行音乐情感分类;

(2)多分类SVM能区分音乐的主旋律;

(3)音程差统计的数据能将流行情感音乐的比例进行分类.

2 模型的建立

音乐分类的处理过程应该符合模式识别应用的一般处理过程，因而可以用模式识别的思想来设计音乐分类技术流程.SVM的理论特色及其在实际应用中的表现，已成为机器学习中一个极具前途的研究领域，备受国内外学者的关注，也成为继神经网之后机器学习领域的研究热点.这在很大程度上解决了模型选择，非线性与维数问题，局部极小值问题等.对于线性不可分问题有两种解决途径，一是一般线性优化问题，引入松弛变量;二是V.Vapnik的引入和空间理论即将低维输入空间中的数据通过非线性函数映射到高位属性空间H(也称为特征空间)，将分类问题转化到属性空间进行.可以证明，如果选用适当的映射函数，输入空间线性不可分割问题在属性空间将转化为线性可分问题.属性空间中向量的点积运算与输入空间的核函数(kernel function)对应.从理论上讲，满足Mercer条件的对称函数K(x，x)都可作为核函数.目前使用的核函数主要有四类:线性核函数、p阶多项式核函数、多层感知器核函数和RBF核函数.

引入核函数之后，最优分类函数的优化问题转化为:

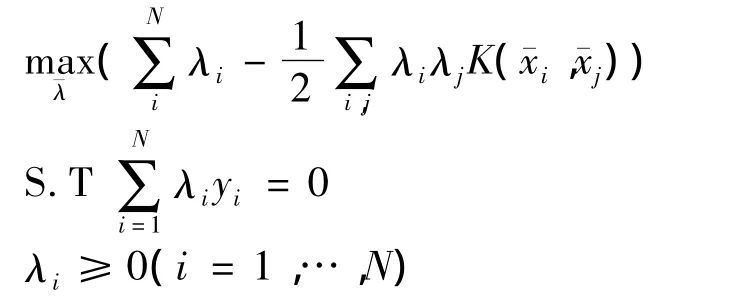
由此得到最优分类函数为:

这就是所谓的SVM模型.从上面的讨论中看出，在模式识别领域具体应用SVM的步骤为:

(1)选择适当的核函数.

(2)求解优化方程，获得支持向量及相应的Lagrange算子［6］.

(3)写出最优分界面方程.

图1为SVM的图样.

图1 SVM的图解

其中:线性判别函数

一个线性判别函数(discriminant function)是指由x的各个分量的线性组合而成的函数.

两类情况:对于两类问题的决策规则为

如果g(x)＞0，则判定x属于C1，

如果g(x)＜0，则判定x属于C2，

如果g(x)=0，则可以将x任意分到某一类或者拒绝判定.

常用的核函数有线性核函数(Linear)，多项式核函数(Polynomial)，径向基核函数(Radial Basis Function，RBF)，S形核函数(Sigmoid)等等.该文采用线性核函数，经典的线性核函数，分类线方程为x*ω+b=0，可以对其进行归一化，使得对线性可分的样本集(xi，yi)，i=1，…，n，x∈R，y∈{－1，1}满足:

在线性不可分的情况下，可以在条件中增加一个松弛项，ξi≥0成为将目标改为:其中ω2是使VC维的上界最小，ξi是松弛项，c＞0是一个常数.

3 音乐情感研究

音程差统计是解析MIDI并对其进行研究的必要条件之一.以音程差统计得到的数据为依据，对MIDI音乐文件进行主音轨定位，主旋律识别和乐段分割等一系列操作.通过分析音程差统计，以不同的音程差值所占的比例为依据，利用一对多思想构造多分类SVM分类器，从而进行流行音乐情感分类研究.仿真实验结果表明该方法具有更好的抗干扰能力和正确率.

基于音乐特征空间的特征建模问题，对计算机自动识别音乐情感的关键技术进行了分析研究.针对多音轨MIDI音乐文档，提出了一种基于改进型音程差统计算法的主旋律音轨自动定位方法.通过对MIDI文件格式的深入分析，提取了表征各音轨旋律声学特征的基本参数(时值，音高，音强等);探讨了旋律音符声学特征与音乐情感描述间的关系，并总结出了基于旋律音符声学特征的音乐旋律情感描述模型如图2所示.［7］

图2 旋律情感特征矢量通用提取模型

基于主旋律的不同，采用音程差统计的方法对不同的MIDI旋律进行了判别，选取100首具有代表性的不同流行歌曲的主旋律进行了音程差统计，如图3所示，其中系列1为“单身的”，系列2为“媚惑的”，系列3为“沧桑的”，系列4为“迷茫的”.

图3 不同主旋律的音程差统计分布图

图3是对音乐情感分类的研究音程差的统计特征为依据，将流行音乐所表达的主旋律主要分为四类，分别为“单身的”，“沧桑的”，“媚惑的”和“迷茫的”.将由音乐学院学生提供的100首比较有代表性的音乐作为样本，其中，“单身的”音乐有16首，“沧桑的”音乐有28首，“媚惑的”音乐有24首，“迷茫的”音乐有32首，每首音乐进行音程差统计，并对解析后所得到的样本数据进行对比分析，然后发现在通过音程差统计得到的数据当中，音程差值比较低的数据所占的比率越大，则这首音乐的主要情感越趋向于“媚惑的”;而音程差值较低的数据所占的比率越小，则这首音乐的主要情感越趋向于“沧桑的”.由于大跨度音程差的频繁出现并不能给音乐增加流畅感，相反会让人感到突兀.因此在音主旋律中纯一度、小二度、大二度、小三度、大三度的旋律音程差所占比率很高，而八度以上的音程差出现较少，对应的音程差值也主要集中在0到6之间.在音程差统计数据中，对于具有不同主旋律的音乐在相同的音程差值上所占的比率范围也存在差异.具体结果如表1所示.

表1 不同情感音乐的音程差统计对比

其中，消极的包括部分“沧桑的”、“媚惑的”、“迷茫的”，积极的也包括部分“媚惑的”、“迷茫的”、“单身的”、“沧桑的”.

4 结束语

情感音乐的分类在计算机多媒体的应用中有着重要的作用，基于对流行音乐的情感分类，该文采用一种SVM模型和线形核函数结合的方法对流行音乐的情感进行分类，利用MIDI的音程差统计算法对音乐的主旋律音轨自动定位方法，通过MIDI的深入分析，提取了表征个音轨旋律声学特征的基本参数.该文的创新点在于采用了一对多的方法，对情感音乐进行了分类，对音乐的主旋律音轨自动定位，难点是核函数的建立及其公式，重点在于对音乐的音轨旋律声学特征参数的提取.音乐情感分类的方法也有许多种，只是采取了其中的一种对音乐进行了划分，对于核函数的应用，还有多层感知器核函数、P阶多项式核函数、RBF核函数.在以后还可以继续向这方面发展.

［1］ 张琴琴.音乐与情感［J］.菏泽师专学报，1993:36－37.

［2］ 曹政，陈宁，王吉军.基于多分类SVM和MIDI音乐情感分类，辽宁，沈阳.

［3］ 李剑.神经网络在音乐分类中的应用研究［D］.重庆:重庆工程职业技术学院，400037.

［4］ 彭琼.计算机自动识别音乐情感的关键技术研究.上海交通大学.图像通信与信息处理研究所，上海.

［5］ 姚斯强，胡剑凌.线性判别分析和支持向量机的音乐分类方法.上海交通大学，图上通信与信息处理研究所.上海交通大学硕士学位论文.

［6］ 曹兆龙.基于支持向量机的多分类算法研究［D］.华东师范大学硕士论文.

［7］ 王鑫，刘军.音乐情感的语言体计算模型的研究［J］.北京邮电大学学报.