空间变系数模型的局部非线性估计
程鹏鹏
(东北林业大学)
0 引言
变系数模型是经典线性模型的一个有用推广,它在诸如地理学、经济学、环境学、生态学、气流学及流行病学等众多领域中有广泛的应用,由于其灵活性以及易于解释性,过去几十年来,变系数模型无论在理论体系还是在应用方面都得到长足发展[1].1996年Brunsdon等首次通过假定线性回归模型中的回归系数是观测点空间位置的函数,将数据的空间位置信息纳入到模型之中,给出了空间变系数模型的概念.并提出以观测点之间的距离的函数为权值的非参数光滑估计方法,称之为地理加权回归方法,简称GWR. Wang等(2008)将变系数模型的局部线性拟合方法推广到空间变系数模型,给出局部线性GWR拟合方法,并通过数值模拟说明改进的拟合方法可以显著的降低系数估计的偏和边界效应[7].
空间变系数模型在短短的十多年中很快得到研究工作者,尤其是实际领域的数据分析工作者的重视.魏传华和梅长林[2]以及魏传华和吴喜之[3]都对这一模型理论部分有进一步的研究.王晨亮和岳天祥等[4]在中国气候的模拟研究中利用了空间变系数模型.LüShiqin and Lu Zhunwei[5]给出了半变系数模型在线性约束条件下的估计以及Zhang Yu[6]在变系数模型的相关理论基础上提出了两种估计方法.
基于空间变系数模型的局部线性GWR拟合方法的基础上,给出了空间变系数模型的局部非线性GWR拟合方法,并进一步得到了模型参数的估计值和偏导数,明确了曲面参数的意义.
1 预备知识
空间变系数回归模型为:

其中βi(u,v)(j=0,1,2,…,p)为空间地理位置(u,v)的未知函数;εi(i=1,2,…,n)为独立同分布的误差项,且E(εi)=0,Var(εi)=σ2[7].
2 空间变系数模型的局部非线性拟合及GWR估计
为简化表示,将空间变系数模型(1)改写为如下形式:

设其中的每个系数函数βj(u,v)(j=1,2,…,p)关于空间位置坐标u和v均有连续的二阶偏导数,这里(u,v)为在某直角坐标系下的空间位置坐标.给定所研究区域内的任一点(u0,v0),对于每个j=1,2,…,p应用Taylor公式对βj(u,v)在(u0,v0)的邻域内进行二阶泰勒展开,并用二次函数逼近,有

达到最小,便得到各空间变系数模型系数函数βj(u,v)(j=1,2,…,p)在(u0,v0)点的局部估计值.其中(Yi;Xi1,Xi2,…,Xip)为因变量Y和自变量X1,X2,…,Xp在地理位置(ui,vi)处的观测值,d0i为(u0,v0)到(ui,vi)的距离,这里

其中K(·)为核函数,核函数选取方法通常为Gauss核或Epanechnikov核,h是光滑参数.
若令
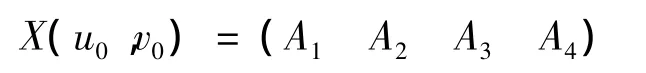
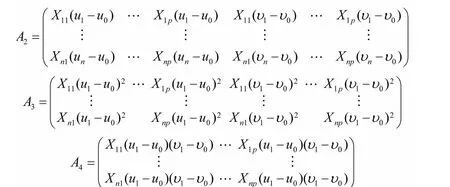

则上述最小二乘问题的解可用矩阵表示为

其中(u0,v0)点的权矩阵和因变量Y在n个观测位置处的观测值所成的列向量.记
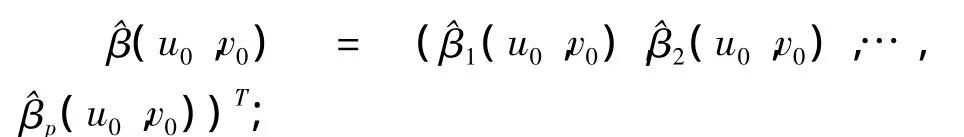
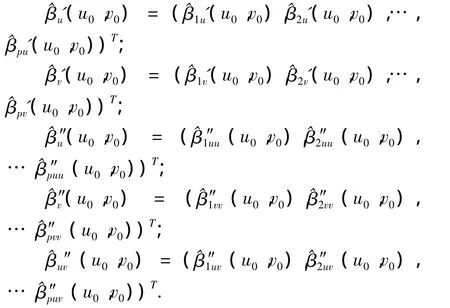
分别为各回归系数函数在(u0,v0)处的估计值所构成的列向量以及关于u和v的偏导数的估计值所成的列向量,则由(3)式可得
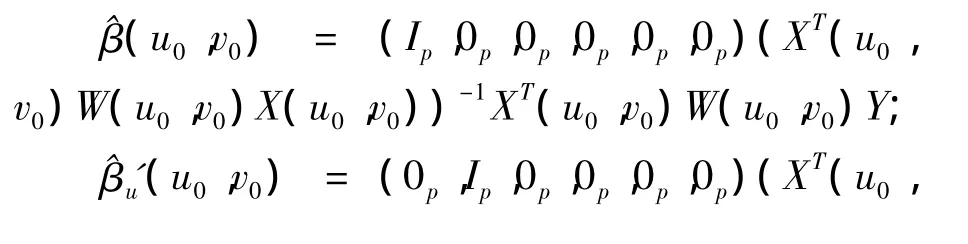
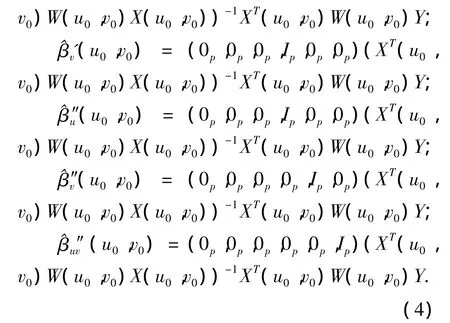
其中Ip和0p分别表示p阶单位阵和p阶零矩阵,令(u0,v0)=(ui,vi),i=1,2,…,n),则由(4)得到模型参数在各观测位置处的估计值为

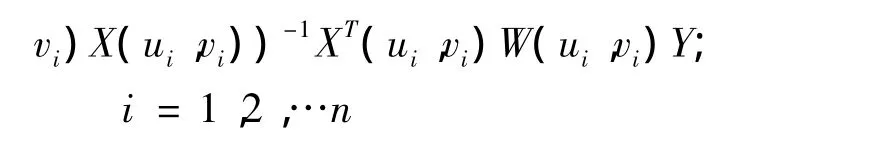
为表示简洁,将五个p阶零矩阵合并为一个p× 5p阶的零矩阵,并用0p×5p表示.由此可得因变量Y在各观测位置(ui,vi)处的拟合值为

其中 Xi=(Xi1,Xi2,…,Xip)T为自变量 X1,X2,…,Xp的第i组观测值所成的列向量.从而因变量Y在n个观测位置处的拟合向量为
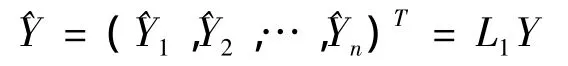
其中
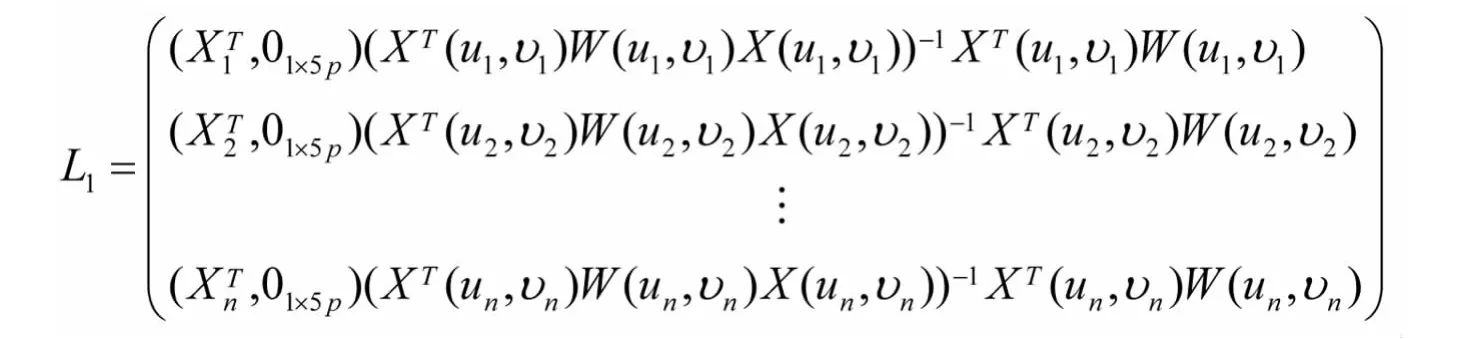
进一步可得局部非线性GWR估计的残差向量为

残差平方和为

由此可得模型(2)的误差方差Var(εi)=σ2的估计为
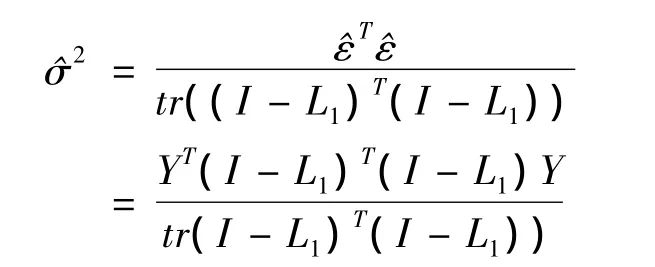
这里光滑参数h的确定方法,可使用CV,GCV或AICc准则确定.
称上述方法为空间变系数模型的局部非线性GWR估计方法,此方法不仅可以得到各空间变系数模型系数函数在区域内任一点(u0,v0)处的估计值,同时也能得到系数函数曲面关于空间坐标u和v的一阶和二阶偏导数在该处的估计值.一阶偏导数在(u0,v0)点的估计值分别反映了系数曲面在该点处沿地理空间坐标u和v方向的瞬间变化率,二阶偏导数能反映变化率的增减性以及曲面的凹凸程度.
3 结束语
对空间变系数模型进行探讨,是经典线性模型的一种扩展.为了使空间地理位置更明确,更形象,将从非线性二次函数拟合以及GWR方法入手,在局部线性拟合基础上推广到局部非线性二次函数拟和,更加深入阐述地理空间位置对变系数的影响.
[1] 许健,刘万荣.广义空间变系数模型[D].湖南师范大学,2009.
[2] 魏传华,梅长林.半参数空间变系数回归模型的Back-Fitting估计[J].数学的实践与认识,2006(3):177-184.
[3] 魏传华,吴喜之.空间变系数模型的统计诊断[J].数理统计与管理,2007(11):1027-1033.
[4] 王晨亮,岳天祥,范泽孟,等.高精度曲面建模的中国气候降尺度模型[J].地球信息科学学报,2012,10:599-610.
[5] LüShiqin,Lu Zhunwei.The Asymptotic Normality Of Constrained Profile Least-Squares Estimation On Semivarying Coefficient Models[J].Mathematica Applicata,2008,21 (1):149-155.
[6] Zhang Yu.B-spline Estimation For Varying-Coefficient Single-Index Model[J].Chinese Journal of Applied Probability and Statistics,2013(8):433-442.
[7] 梅长林,王宁.近代回归分析方法[M].北京:科学出版社,2012.

