基于Bootstrap法的BCa区间二阶矫正性质研究

刘 薇，常振海，张德生

（1.天水师范学院数学与统计学院，甘肃天水741001；2.西安理工大学理学院，陕西西安710054）

基于Bootstrap法的BCa区间二阶矫正性质研究

刘 薇1，常振海1，张德生2

（1.天水师范学院数学与统计学院，甘肃天水741001；2.西安理工大学理学院，陕西西安710054）

首先，证明了基于Bootstrap法的BCa区间二阶矫正性质的相关抽象结论；其次，讨论了BCa区间的算法实现，并进行了实证分析。结果表明，在分布左尾较长的情形下，分位数法将正态区间的端点向左调整，BCa法又将分位数区间端点进一步向左调整，区间对称性也从正态区间的1，调整至分位数区间的0.58和BCa区间的0.38。这些调整均说明BCa区间是最为符合分布特性的估计区间，印证了BCa区间的优良二阶性质。

Bootstrap法；BCa区间；二阶修正性；二阶精确性

近些年来，Bootstrap方法因为其优良的统计性质一直是众多相关学者关注的热点之一，如文献［1－4］从不同领域、不同方面展示了Bootstrap方法及其应用。基于Bootstrap方法的区间估计是其应用方面之一。

依据文献［5，6］关于BCa区间的高度概括和抽象的结论，我们首先简化了基于Bootstrap法的BCa区间二阶矫正性质。然后讨论了BCa区间的算法实现，并进行了实证分析，印证了BCa区间的优良二阶性质。

1 二阶性质

2 实证分析

实例数据来源于Bootstrap法的发明者Bradley Efron所用数据［5］，目的是用抽取的15对样本数据去估计总体（共82对数据）的相关系数，本文进一步分析了相关系数的BCa置信区间。总体数据和随机抽取的样本数据见图1。运算基于Matlab 7.5。

图1 总体数据点和样本数据点

图2 Bootstrap法相关系数分布图

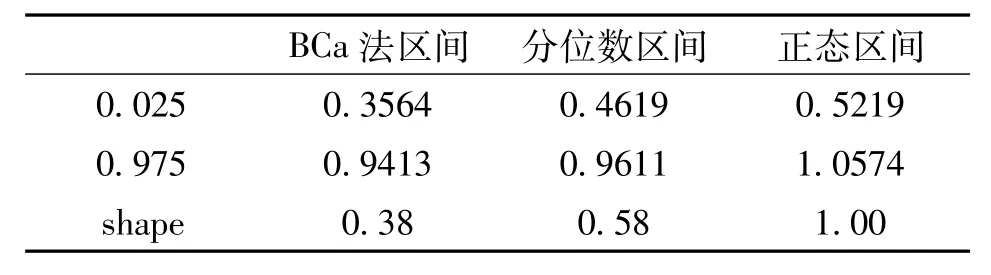
表1 三个非参数Bootstrap法置信区间

从表1能看出，非参数Bootstrap分位数法把上下区间端点分别从1.0574和0.5219调整到了0.9611和0.4619；BCa法则进一步把分位数区间上下分位点分别调整到了0.9413和0.3564。而shape则从1减小到了0.38。为了直观的说明这些调整过程，把BCa法区间和分位数区间显示在了图3中。

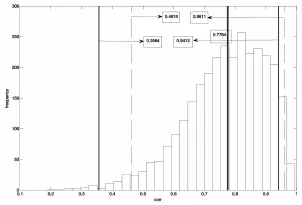
图3 Bootstrap法相关系数分布图及相关置信区间

从图3能直观的看出，BCa法的调整更加符合分布左尾较长这个特性，从而是较适合的估计区间。

3 结论

（1）文献［5，6］中关于BCa的高度概括和抽象的结论不利于人们对BCa区间优良性质的理解，本文首先从理论上简化了基于Bootstrap法的BCa区间二阶修正性这个性质，它甚至把上端点延伸到了1之外，所以它的这个性质在总体不对称的时候是十分有害的。因为分布左边尾巴较长，所以分位数区间的shape＝0.58就比1小了很多，应该说比正态区间好多了，而BCa法区间的shape＝0.38，比分位数区间的还小，就更加符合分布的左尾较长这个分布特性，应该说是较适合的区间。

（3）需要指出的是，本文证明二阶性质时是从总体均值入手证明的。对于更加复杂的总体参数形式或总体参数的函数的二阶性质的证明，方法类似，只不过矫正参数a，z0的表达式应该和文中的不一样。

另外，BCa区间需要再抽样次数较大才能起到有效的作用［6］，一般要在B＝2000以上，本文为3000，对于这个不足之处本文没有过多强调，这个缺陷现在计算机较为发达的今天不是问题，同时也可以考虑ABC法区间［5，7］，详见相关论文。

［1］Shuang Li，Li Hsu，Jie Peng.Bootstrap inference for network construction with an application to a breast cancermicroarray study［J］.Annals of Applied Statistics，2013，7（1）：391－417.

［2］Xiaofeng Shao，Dimitris N.Politis.Fixed b subsampling and the block bootstrap：improved confidence sets based on pvalue Calibration［J］.J.R.Statist.Soc.B，2013，75（1）：161－184.

［3］Guosheng Yin.Pearson－type goodness－of－fit test with bootstrap maximum likelihood estimation［J］.Electronic Journal of Statistics，2013，7：412－427.

［4］金浩，张思，乔宝明，等.基于Bootstrap的厚尾相依序列持久性变点检验［J］.数学的实践与认识，2012，43（13）：174－179.

［5］Efron B，Tibshirani R J.An Introduction to the Bootstrap［M］.New York：Chapman＆Hall Ltd，1993.

［6］DiCiccio J，Efron B.Bootstrap confidence intervals［J］.Statistical Science，1996，11（3）：189－228.

［7］DiCiccio J，Efron B.More accurate confidence intervals in exponential families［J］.Biometrika，1992，79：231－245.

［责任编辑 毕 伟］

Second－Order Correct Properties of BCa Interval Based on the Bootstrap M ethod

LIUWEI1，CHANG Zhen-hai1，ZHANG De-sheng2
（1.School of Mathematics and Statistics，Tianshui Normal University，Tianshui741001，China；2.School of Science，Xian University and Technology，Xian 710054，China）

Firstly，abstract conclusions of second－order correct property of BCa interval based on bootstrap method are simplified.Then，BCa interval algorithm is discussed，and example is used to show how this is done.The results show，in the case of long left tail distribution，standard interval endpoint is adjusted to the leftby percentilemethod，and percentile interval endpoint is further adjusted to the left by BCamethod；The shape about symmetry of standard interval is adjusted from 1to percentile interval＇s0.58，and further to BCa interval＇s0.38.These adjustments show that BCa estimation interval is themost consistentwith distribution characteristics，which also confirm excellent second－order properties of BCa interval.

Bootstrap method；BCa interval；second－order correct；second－order accuracy

O212.1

A

1004－602X（2014）04－0008－02

10.3969／J.ISSN.1004－602X.2014.04.008

2014-10-20

国家自然基金（51379173）；天水师范学院中青年教师科研资助项目（TSY201204）

刘 薇（1980—），女，河南卢氏人，天水师范学院讲师。