从负折射超材料到光学隐身衣

黄志洵

(中国传媒大学信息工程学院，北京 100024)

1 引言

负折射率的英文是negative refraction index，简写为NRI，指的是一种光线在界面上向与常规不同方向折射的现象。折射率用n表示，它与相速vp相联系。相速是根据理想的等幅单色波信号［Acos(ωt-kz+φ)］而定义的，这种时间上没有开始也没有结尾(即t从负无限大到无限大)的等幅信号在现实中并不存在，因而人们怀疑相速的意义，从而更看重群速的作用。然而，近年来对负折射率(因而也是对负相速)研究的日益成功，不仅确认了负折射现象的存在并发掘了多方面的应用，而且也彰显了相速的地位，这是人们始料不及的。理论和实验都已证明，电磁波向正常媒质/超材料界面入射时，在超材料(也称左手材料)中折射波方向和入射波方向处在法线的同一边，即发生了与过去习惯方向不同的偏折。因而后来人们不再争论，而是在确认负折射现象存在的基础上探索更深入的规律，直到开始研究微波乃至光频的隐身衣;在这过程中对负折射的理论认识得到了深入。

2 早期研究工作

1964年前苏联物理学家V.G.Vesselago的论文“ε和μ同时为负的物质的电动力学”用俄文发表(见:Usp.Fiz.Nauk.，Vol.92，July 1964，517 ～ 526)。1968年美国人将其译为英文重新刊出［1］。这篇文章奠定了“媒质负电磁参数研究”的理论基础。然而在后来的30多年中，此文未受重视，既未出现相关的实验，也没有进一步的理论工作。1996年J.Pendry［2］提出，如把众多细而直的金属丝(丝径 d、丝间距a)均匀、立体地排列，则在入射电磁波波长λ≫a≫d时，若电场与丝同方向，则等效介电常数为负(ε ＜0)。1999 年 J.Pendry［3］提出了开口谐振环(SRR)系统，并证明在一定频带内等效磁导率为负(μ＜0)。这就出现了实现Vesselago思想的可能性。2000年春美国UCSD的科学家宣布做成了“负折射率实验”，就是用Pendry方法。相关的论文的第一作者是 D.R.Smith［4］，题目是“介电常数和导磁率同时为负的复合媒质”。2001年又发表了两篇论文，一个是 R.A.Shelby等［5］的论文“负折射率的实验证明”，另一个是 D.R.Smith等［6］的论文“左手材料中的负折射率”。此后，相关研究在各国广泛开展起来。在中国，笔者当时敏感地意识到这个方向的重要性，于2001年秋发表了介绍负折射研究文章，题为“微波异常传播中的负折射率问题”［7］，它可能是中国人在此领域的首篇论文。

Pendry—Smith型方法是在微波获得LHM，先在(4.2～4.6)GHz成功，后在 X 波段(8.2 ～12.4)GHz实现。以后，几年中陆续出现了一系列研究工作:2002 年 G.Eleftheriades［8］建议由另一途径设计这种媒质，使用人们熟知的LC分布参数网络以描写均匀介质;这样就出现了左手传输线(left-handed transmission line，LHTL)概念。2003 年 N.C.Panoiu等［9］发表了“远红外和光频时负折射超材料的数据研究”文章，可能是把LHM置于光频条件下的最早研究。2003至2004年间，出现了与Pendry—Smith方法不同的尝试——企图用光子晶体(PC)技术达到同样目的，例如Page等用PC实现LHM功能对超声波实现了负折射［10］;这就再次证明为了获得NRI并非依靠单一的方法。2005年 A.Grigorenko首次在光频制成了具有负导磁率的超材料［11］。2007年1月，M.Wegener在红光波长(约700nm)使材料具有负折射率(n=-0.6)［11］。2006 年 J.Pendry［12］在《Science》上发表文章，预言超材料可用来设计使物体隐形的invisibility cloaks(隐身斗篷)，开辟了一个新方向;它可称为电磁隐身衣(EMIC)或光学隐身衣(OIC)。同年，D.Schurig 等［13］在微波验证了EMIC的思想，其证明限于2D结构。2008年J.Yao等［14］用纳米技术首次实现了可见光频段的超材料和负折射。因此在可见光的努力始于2003年，获得突破是在2008年;而后来的目标是研制3D

3 基本理论关系

在研究工作中必须对基本的理论关系有明晰的理解。2012年黄志洵［15］提出“三负研究”的概念，那么负折射研究与负波速研究具有怎样的关系?如所周知相折射率n和群折率ng的定义为

式中c是真空中光速，vp、vg为相速、群速。显然，研究负相速(NPV)和研究负折射率(NRI)是一回事，研究负群速(NGV)和研究负群折射率(NGRI)是一回事。这些简单的概念有时被忽视，从而得到错误的结论。例如，近年来有关NGV的实验甚多［16～20］，直接做NPV实验似乎只有K.Wynne等［21］于2000年用微小孔径圆截止波导的测量。但这种看法是错误的，因为自2001年以来全世界出现了上百个研究NRI的小组，他们的工作本质上也是探索NPV。可否用超材料获得NGV?为回答这个问题，需要考虑n和ng的关系。

2002年 P.M.Valanju 等［22］认为人们错误地解释了“光的负折射”，因为在LHM中群折射率是正值而非负值(ng＞0)，即垂直于群波前的物理射线是正折射的;他实际上是否定负折射研究的意义。笔者早已指出他的意见是错误的［23］，这里再作些分析。

ng和n的关系为

假设实验人员面对一个LHM，则n＜0;这时如为反常色散(dn/df＜0)，肯定有ng＜0。即使正常色散(dn/df＞0)，在一定条件下也出现负的群折射(ng＜0)，这个条件是

因此Valanju等人的观点是错误的;实际上对超材料而言容易获得负的群折射率和负群速，具体如何实施则是实验设计上的技术问题。……Valanju曾根据 Shelby［5］的数据(n=-3.67+j0.091)算出 ng=186.44-j7，即在 Ren＜0 时会有 Reng＞0(相折射为负时群折射为正);笔者认为这并不奇怪，因为ng并不等于n，而受另一项(f dn/df)的影响。但这现在我们不仅知道超材料即负折射(相折射)材料或负相速材料，LHM的含义等同于NPV;而且又知道为获取NGV确实可以选用LHM，但NGV不等同于LHM。也就是说，不能讲NGV一定代表某种物质，而是在物质的不同形态下(如原子气室、光纤、超材料)可能获得的物理现象。对于企图做NPV实验的人而言，完全可以着手制备LHM作为开端。

图1表示一个有宽度的波束入射到媒质1、媒质2相交的界面，两条射线(AC和FB)代表这个波束，虚线是相波前。假定两媒质均为常态物质(RHM)，在n2＞n1时波束在媒质2中被折射为和，即折射角 θ2＜ θ1，而是相波前。所谓负折射发生在媒质2为LHM时，这时波束成为和是相波前;而这时相速的方向用上面的小箭头表示，因为相速的方向是波矢的方向，而在LHM中与Poynting矢方向相反。……不过图1的入射波应是等幅波;如入射波为脉冲波，如何绘制群折射图形还当另作考虑。

图1 发生在物质界面上的情况

让我们换个角度思考，提出的问题是“双负媒质(ε＜0、μ＜0)与负折射媒质(n＜0)是否等同”?由Maxwell波方程可导出

故得

等式右端的负号不能随便舍弃。

假定LHM有损耗，并且用电导率σ代表这一损耗的存在，上述命题可以作直接的推导。对有耗媒质取 εc= εrcε0，那么就有

这时波矢大小的平方为

然而当取 k=-jγ =β -jα 时，就有

两式对照，可得一个联立的代数方程:

对于一个无源媒质，α＜0是不可能的，因这意味着放大功能，故α公式应取正号。问题是β的符号应怎样取?对RHM，μr＞0，因而b＞0;我们知道波传播的相速(因而相位常数)必定是正值，故β＞0。对LHM，εr＜0，因而 b＜0;假定 LHM 无耗(σ =0)，这时b=0，由(9)式得 α=0，由(10)式得但由(8)式知这时k=β，故有k=±k0;但LHM造成负相速(NPV)，而这导致负相位常数，故得

因而使用折射率参数时有

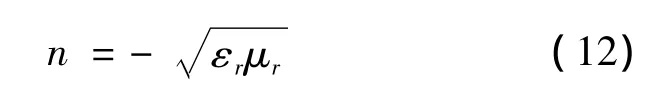
这就从逻辑上得到双负材料LHM的特性:当εr＜0、μr＜0，根号内两者相乘为正值，而折射率n为负值。

总之，获得负折射率的条件是介电常数和导磁率均为负数，二者缺一不可。以下用计算数据和实验数据作进一步的说明。令

已知在一定条件下等离子体和金属可能出现负介电常数，故可把(13)式改写为

假定μr=1，则有n2=εr;在这种情况下可得下述联立方程:

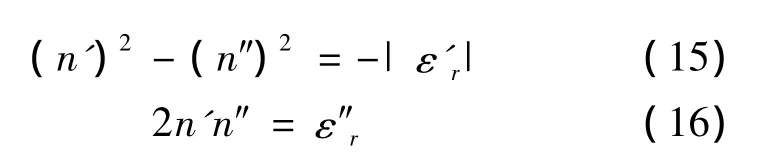
故 n'、n″可求;例如我们取 ε'r=-13.4，ε″r=1.4;可算出 n=0.19+j3.6，n'和 n″均为正值。故仅有 ε ＜0并不能得到n＜0，即单独的负介电常数对于负折射的获得是不够的，但它却是必须的。虽然这是在特殊假定(μr=1)之下作的计算，但仍能说明问题。

D.Smith［6］曾作过一个计算，根据 SRR 和导线的简单组合算出了一组数据。计算中又取μr=μ'r+jμ″r;对于 ε'r，它在(5 ～ 12.5)GHz 为负，(12.5 ～ 14)GHz为正。至于 μ'r，它在(4 ～8.5)GHz及(9 ～14)GHz为正，(8.5～9)GHz为负。在这种情况下，只有在(8.5～9)GHz才有n'＜0，其余频率上均为n'＞0;这与理论预期一致。在图2中，(a)是介电常数实部，(b)是导磁率实部，(c)是折射率实部。可见，在(8.5～9)GHz得到了 ε'r＜0 和 μ'r＜0，因而得到 n'＜0。

图2 由微波网络参数算得的εr、μr和n的实部

计算还证明，使用Pendry—Smith方法(用导线阵与SRR群组成LHM)，可以在红外区获得超材料。图3是相关研究的结果［9］，在宽阔频域(130～160THz)折射率的实部为负。认识到负折射效应并不限于微波是重要的。

图3 红外区LHM的相折射率

4 基本实验方法

尽管上述分析言之有理，但仍然需要一种直接的折射率测量，也需要有对折射角为负的直接证明。2001年7月的《中国工程科学》杂志在封面刊出了一个图，是笔者推荐的;“封面说明”也是笔者所写，其中说:“2001年4月6日在《Science》发表了题为‘负折射率的实验证明’论文。《中国工程科学》本期封面图即为RHM和LHM的测量装置示意:被测样品做成棱镜形，置于两块圆铝板之间，黄色箭头表示来波方向和折射方向;微波检测器装在可旋转架上，故可测出RHM、LHM与折射角θ的关系。由于负折射率是由介电常数ε＜0、导磁率μ＜0造成的，故此实验亦可视为负能量的实验，并与超光速问题相关联。”

图4是这个测量装置的图形，被测样品(棱镜)置于两块圆形铝板(直径30cm)之间，板距1.2cm。粗黑箭头表示来波方向和折射(按n＞0)方向。检测器是用X频段波导连接微波功率测量装置，实际上是用波导—同轴转换器及HP8756A型标量网络分析仪。微波波束从棱镜射出时，表面为折射界面(按Snell定律规定的角度方向)。现在把检测器安装在可旋转的架子上(1.5°步进)，这时试验人员就可以对RHM、LHM分别测量接收电平与角度(θ)的关系，并作比较。图5是取频率f=10.5GHz时接收电平与折射角的关系，为了方便把两种样品的峰值电平都归一化为1。结果是，对于常规材料(RHM)的 Teflon，峰值发生在 27°处，对应 n=1.4 ±0.1;对于LHM系统，峰值发生在-61°处，对应n=-2.7±0.1。可见，在LHM情况下，折射角与RHM相差88°(接近 π/2即90°)。故在一定频率(满足 LHM要求的频率)下，折射角按与Snell定律指示的不同方向偏转，呈现n＜0。

图4RHM和LHM的测量装置

图5 接收功率归一化值与折射角的关系

图6是折射率与频率的关系，实线是可能出现LHM现象的材料，虚线是作为对比的一种电介质(Teflon)的情况。当 f为 10.2GHz～10.8GHz、LHM处在负折射率频区，且有高度色散性。图5和图6均为早期实验成果，但它们宣示了Veselago理论的正确。

图6 折射率与频率的关系(实验值)

5 关于左手传输线

2002年 G.V.Eleftheriades等［8］提出左手传输线(LHTL)概念，后来逐步成型［24，25］，其根据是电磁波方程与传输线方程在形式上有相似的地方，因而用电压电流在周期性电路结构中的传播模拟电磁波在媒质中的传播。在LHTL中，串联电抗和并联电纳为负可以用一定方法实现，并由此发展了等效传输线(电路结构)的等效介电常数(εeff)和等效导磁率(μeff)的模拟参数和分析方法。

单色波条件下Maxwell第一旋度定律为

亦即

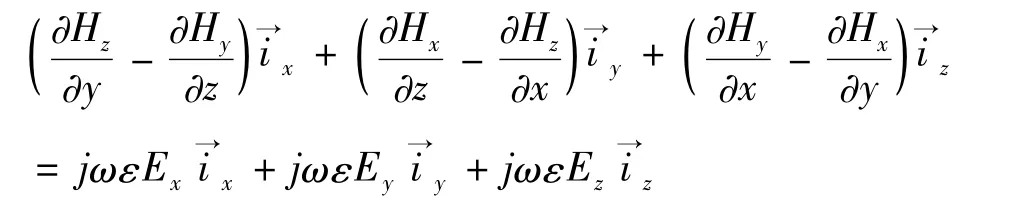
取一维情况，即波传播方向为z向;故取∂/∂x=0，∂/∂y=0，故有

类似地，由Maxwell方程组的第二旋度定律可证:

因此得到一对偏微分方程:

然而在传输线理论中无耗时的经典电报员方程为［35］

式中 L、C 为沿线的单位长自感、电容;取 i=Iejωt，u=Uejωt，则可推出:

这与方程组(17)极为相似。如把Hy与u、Ex与i相对应，立即看出ε与L、μ与C相对应。故Vesalago的双负参数(ε＜0，μ＜0)理论，可移植到传输线中来。只要设法使L＜0、C＜0，就得到与LHM对应的LHTL。

这个方法在原理上是简单的——图7(a)表示右手传输线(RHTL)的基本单元，图7(b)表示左手传输线的基本单元。对后者，并联导纳YL=1/jωLL，串联阻抗 ZL=1/jωCL，故有

这就满足了LHM的基本要求。

实际上LHTL常用微带实现，在谐振腔、带通滤波器、微带漏波天线等方面的应用都令人感兴趣。

6 负折射的宽频域特性

虽然LHM的实验是在微波取得突破，但不说明只有这个波段才会发生负折射现象。例如2004年有报道说［10］，J.Page把负折射概念用到了超声波领域，实现了“负的声折射”(negative sound refraction);用的材料是一种，是用碳化钨珠做的人工合成结构(a synthetic structure made of tung-sten carbide beads)。物理学家早就知道光子晶体在某些频率上能阻止超声波(block ultrasound)，对Page而言是(0.98 ～1.2)MHz;但他们发现，在稍高的频率上(1.57MHz)，光子晶体使声波弯曲和聚焦，呈现负折射现象。图8显示有关的过程:S是超声源，虚线表示超声波通过一般材料的情况;实线是当使用光子晶体时超声波射线在其中发生负折射随后又聚焦的情况。由此可开发高分辨率超声波扫描技术。

图8 超声波的负折射

自2003年起人们企图在红外和光频获得超材料和负折射，发现要扩展到这样高的频域并非易事。首先，金属介电常数的频率色散变得重要了。其次，当频率高到可与金属等离子振荡频率相比拟，会激发表面等离激子(surface plasmon)，使金属电磁特性有较大改变。另外，建造光频段的负折射超材料的难度在于物质谐振损耗和制作艰难，2005年Grigorenko［11］的工作尚不是真正的进展。

2008年8月15日，《Science》刊登了两篇文章报道美国Berkeley加州大学(UC Berkeley)的有关研究。简短报道刊登在P.900，题为“用于可见光视觉方面的古怪超材料”。文章说，自从2000年人们成功地用金属圆棒和环使微波向奇特方向弯曲以来，在可见光区实现就成了物理学家们的宏伟目标。这结果已由UC Berkeley的Xiang Chang(张翔)的实验室所获得。这个报道是为P.930的文章作介绍，后者题为“用纳米线的块状超材料光学负折射”，作者是 J.Yao 等［14］，他们在多孔以小于可见光波长的微小间距植入银丝()，获得了负折射。这被称为银纳米线超材料(silver nanowire metamaterials，SNM)。图9显示的是众多的线组成矩形块状单元，图中绘出并列的金属线阵，线径60nm，间距110nm;对于入射波束(由空气进入LHM)的波长780nm而言，间距比λ小得多。实验中样品厚度取4.5μm、11μm ，入射角取 θ1=30°，按TE、TM极化分别测量。图9表示入射波束发生负折射的情况，当θ1＞0时有 θ2＜0，而 d表示证明负折射发生的透射位移。图10是测量结果，当取θ1=30°，发现TM时为负折射，TE时为正折射;实验者未说明为何如此。

测量还给出，对TM极化群折射率为(-4)，对TE极化为2.2;然而相折射率(因而相速)保持正值。这是奇怪的，实验者也未作解释。……总结张翔实验室的成绩:在光频制成了超材料并实现了负折射;(vg=-0.25c);其论文说可应用于导波传播、成像、光通信，未提电磁隐身衣(EMIC)和光学隐身衣(OIC)。

图9 纳米导线的超材料示意

图10 光频段超材料实验结果

7 电磁隐身衣和光学隐身衣

英文invisibility cloaks原意是不可见的斗篷，译作隐形斗篷或隐身斗篷是正确的。它是用偏转光波使得人眼看起来物体隐去无踪(Invisibility cloaks work by deflecting light waves so the light that reaches the eye shows no trace of the hidden object)。它也被称为超材料电磁斗篷(metamaterial electromagnetic cloak)，通常叫做电磁隐身衣(EMIC)，如能在光频实现便称为光学隐身衣(OIC)。通常人们对隐身的理解是“人眼看不到物体”，是指在可见光(visible light)波段发生的事。因此，只有光学隐身衣成功才是真正的成功。2006 年 J.Pendry等［12］提出(Transformation Optics，TO)，认为有两个空间:虚拟空间(原空间)，物理空间(变换空间);而Maxwell方程组在不同空间中的形式不变性是隐身衣设计的理论基础。将虚拟空间中的一个实心区域压缩变换到物理空间(现实空间)中的一个空心区域，后者具有metamaterial的各向异性非均匀ε和μ，就是要设计的EMIC。如在物理空间中得到一个球壳状的隐身衣(图11)，电磁波不进入空心区域;球壳对外部电磁环境不产生影响。对这理论预言，同年由美国Duke大学的科学家作了实验验证。具体讲，D.Schurig等［13］在微波设计和制作了一个的EMIC，成功地隐蔽了一个铜圆柱体。实验证明选用人工电磁材料(如LHM)是很好的选择，因为通过设计可以灵活控制它的ε和μ。微波实验证明电磁波在EMIC中平滑地绕过物体(铜圆柱体)区域并在离开EMIC后恢复了原来的波阵面，从而在观察者面前从各方向把物体隐藏起来(that can hide something from would be obsevers in any direction)。

在二维EMIC的研究中，开始时人们集中在旋转对称的结构(球状斗篷或圆柱状斗篷)上，因为理论分析较为容易。2008年李超等［26］研究了对二维任意形状EMIC的设计原理，基于Huygens原理定量分析了散射特性，数值计算证明由于斗篷的存在使导体柱的散射降低了(13～20)dB。2008年10月，《Science》杂志又报道了美国珀杜大学(Padue University)的Saraev领导的一项研究，在一个玻璃轮辐的中心装上许多纳米针，像一个圆形梳子，可以使可见光避开罩在里面的物体。2009年1月，D.Smith用在一块电路板上，构成，是对EMIC研制的又一努力。

图11 球状隐身衣示意

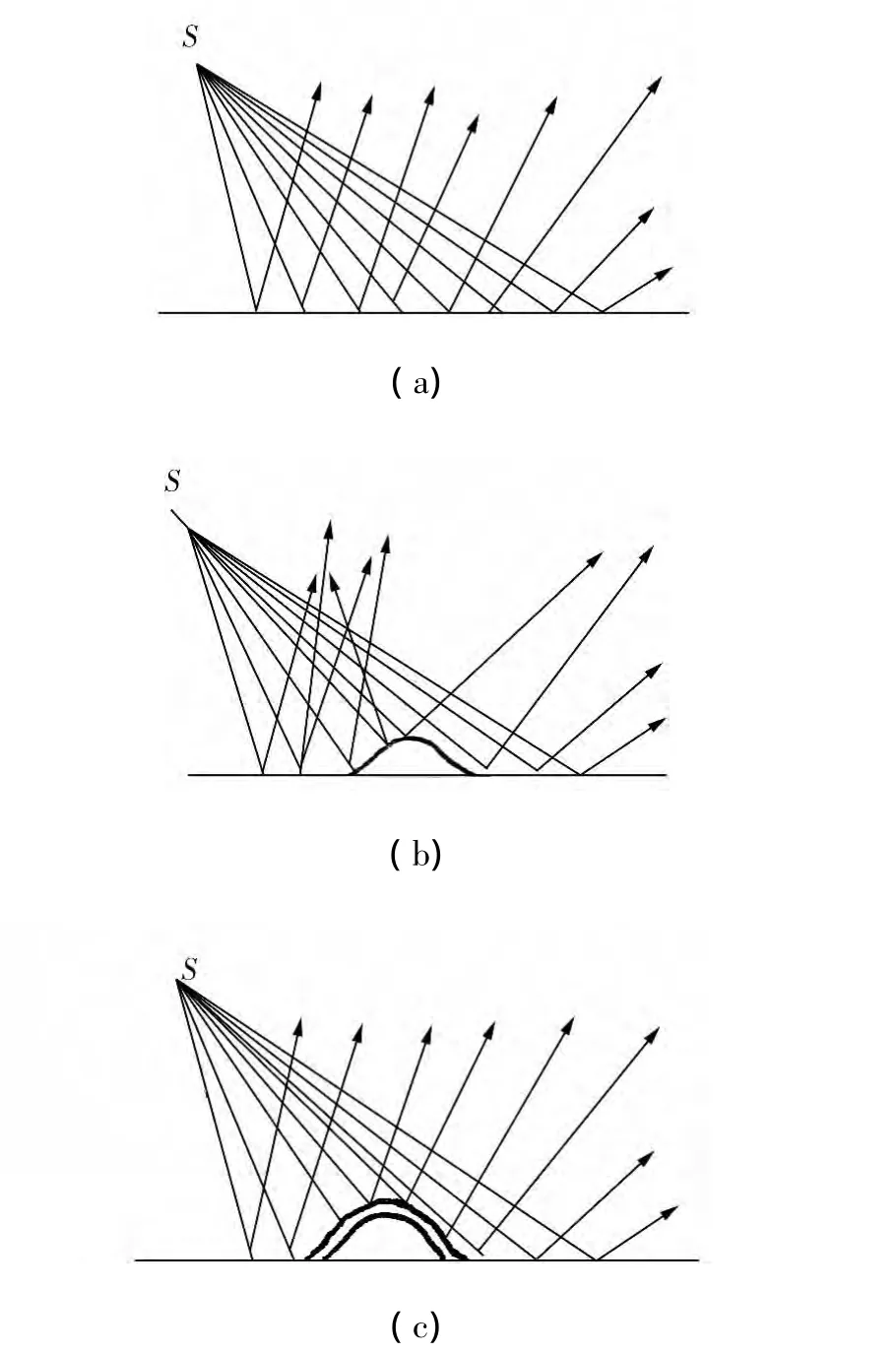
图12 平面上的突起物可以隐身的说明

美国Berkeley加州大学的张翔在美国政府资助下指导两个小组进行研究，其中的一个小组在2008年8月实现了可见光波段的LHM，前文已述。2009年5月下旬在美国Baltimore召开了国际量子电子学会议(International Quantum Electronics Confer-ence)，会上有两篇关于EMIC的报告，谈到在比微波更短波长的红外光波段的研究。两个小组，Berkeley研究组以 J.Li为首，Cornell研究组以 L.Gabrielli为首，他们都是运用纳米技术，方法却不是使被隐藏物周围的光偏转。图12显示，平面上的一个突起物如何会使人“视而不见”——(a)表示入射光以均匀亮度在一个平面上反射;(b)表示突出物使光散射开来并形成阴影;(c)表示加上cloak之后修正了光的漫散射，使当时当地是平面(突出物没有了)。这样的方法是用一个薄层物体来隐藏目标(突起物)，起cloak作用——由于它，光被均匀地反射而无阴影，故被称为“魔毯”(magic carpet)［27］。……这让人想起2008年2月在美国研制的一种吸收材料，它只有一张纸的厚度，但能吸收入射光的 99.955%(it’s very very dark)。它实际上是一种捕获器，由空心纤维制成，它给人一种“什么都没有”的错觉。

2010～2012年期间各国科学家仍在隐身衣这个方向上作持续的努力。2010年3月18日出版的《Science》报道说，欧洲(德国、英国)的研究人员首次实现了隐身斗篷。科学家说，把一个小物体放在所设计的微小结构(EMIC)的下面，它有点像一块反射毯;这时通过透镜进行观察并作光谱研究，从哪个角度都看不到物体了。所谓“微小结构”由构成，它们使光线转向，从而使下面的物体(微小突起)散射的光线消失。他们的EMIC的尺寸是100μm×30μm，突起的尺寸大约是前者的1/10。研究人员认为在宏观尺寸上实现隐身的困难非常大。2010年中国大陆科学家也设计成功光学隐身衣。

2011年7月美国媒体再次报道了UC-Berkeley的张翔的工作，说他用多层二氧化硅(SiO2)和氮化硅(SiN2)做成一件光学隐身衣，从而使物体“在人眼可见光下隐形”成为可能。但被隐物体非常小，只有一个细胞大。2012年12月又报道了加拿大超级隐形生物科技公司的说法，它声称已制成量子隐身材料，并向军方作了演示，它能使军用红外设备失效。

8 结束语

本文是对负折射课题的基础性论述。由于发展太快，我们不能提供情况的研究工作很多。而且，现实是不断有更新颖的方法出现;例如2013年11月有报道说，加拿大多伦多大学的研究人员使用一层小型天线将物体包起来，研发成功一种实用型隐形斗篷，未用超材料。……人类的智慧是无穷尽的;但这并不能消除负折射和超材料研究的意义。因此，我们的态度是乐观的!新方法认为不用超材料是优点，但超材料隐身衣设计者也可以说用不着那么多小天线才是好;究竟如何还有待时间的考验。

［1］Vesselago V G.The electrodynamics of substances with simultaneously negative values of permittivity and permeability［J］.Sov Phys Usp，1968，10(4):509-514.

［2］Pendry J B，et al.Extremely low frequency plasmons in metallic meso structures［J］.Phys Rev Lett，1996，76:4773-4776.

［3］Pendry J B，et al.Magnetism from conductors and enhanced nonlinear phenomena［J］.IEEE Trans MTT，1999，47:2075-2084.

［4］Smith D R，et al.Composite medium simultaneously negative permeability and permittivity［J］.Phys Rev Lett，2000，84(18):4184-4187.

［5］Shelby R A，et al.Experimental verification of the negative refraction index［J］.Science，2001，292(6 Apr):77-79.

［6］Smith D R，Kroll N.Negative refractive index in left-handed materials［J］.Phys Rev Lett，2001，85(14):2933-2936.

［7］黄志洵.微波异常传播中的负折射率问题［J］.物理，2001，30(11):689-692.

［8］Eleftheriades G V，et al.Planar negative refractive index media using periodically LC loaded transmission lines［J］.Trans IEEE，2002，MT50(12):2702-2712.

［9］Panoiu N C，Osgood R M.Numerical investigation of negative refraction index metamaterials at infrared and optical frequencies［J］.Opt Commun，2003，223:331-337.

［10］Mullins J.Bending sound for a sharper scan［J］.New Scientist，2004，(4 Sep):19.

［11］Mullins J.Now you see me［J］.New Scientist，2007，(17 Feb):38-41.

［12］Pendry J B，et al.Controlling electromagnetic fields［J］.Science，2006，312:1780.

［13］Schurig D，et al.Metamaterial electromagnetic cloak at microwave frequencies［J］.Science，2006，314:977-979.

［14］Yao J，et al.Optical negative refraction in bulk metamaterials of nanowires［J］.Science，2008，321(15 Aug):930.

［15］黄志洵.负波速研究进展［J］.前沿科学，2012，6(4):46-66.

［16］Wang L J，Kuzmich A，Dogariu A.gain-asisted superluminal light propagation［J］.Nature，2000，406:277-279.

［17］Gehring G M，et al.Observation of backward pulse propagation through a medium with a negative group velocity［J］.Science，2006，312(12 May):895-897.

［18］Monti G，Tarricone L.Negative group velocity in a split ring resonator-coupled microstrip line［J］.Prog.EM Res，2009，94:33-47.

［19］Zhang L，et al.Superluminal propagation at negative group velocity in optical fibers based on Brillouin lasing oscillation［J］.Phys Rev Lett，2011，107:1-5.

［20］Glasser R T，et al.Stimulated generation of superluminal light pulses via four-wave mixing［J］.ar Xiv:1204，08/0v/［quant ph］，3 Apr 2012，1-5.

［21］Wynne K，et al.Tunneling of single cycle terahertz pulses through waveguides［J］.Opt Commun，2000，176:429-435.

［22］Valanju P M，et al.Wave refraction in negative index media:always positive and very inhomogeneous［J］.Phys Rev Lett，2002，88(18):187401，1-4.

［23］黄志洵.负折射率研究中的若干理论问题［J］.北京广播学院学报(自然科学版)，2005，12(4):1-11.

［24］Iyer A K，et al.Experimental and theoretical verification of focusing in a large periodically loaded transmission line negative refractive index metamaterial［J］.Opt Express，2003，11(7):696-708.

［25］Eletlheriades G V，Siddiqui O F.Negative refraction and focusing in hyperbolic transmission line periodic grids［J］.Trans IEEE，2005，MT53(1):396-403.

［26］Li C，Li F.Two dimensional electromagnetic cloaks with arbitrary geometries［J］.Opt Express，2008，16(7):13414-13416.(又见:李超，李芳.基于人工电磁材料的新型电磁隐身机制——电磁隐身斗篷［J］.北京石油化工学院学报，2009，17(1):48-52.)

［27］Hecht J.Magic carpets can hide objects in plain sight［J］.New Scientist，2009，(13 Jan):20.