大型相控阵雷达天线阵面视情维修优化模型
卢 雷,杨江平,左治方,欧阳林涛
(1.空军预警学院,湖北武汉430019;2.95980部队,湖北襄阳441021)
0 引言
为适应对人造卫星、弹道导弹等目标的监视、跟踪、编目等需要,国内外从20世纪60年代就开始大力发展大型相控阵雷达[1]。与常规地面雷达相比,大型相控阵雷达天线阵面在维修保障方面具有以下特点:一是系统庞大,设备量多,如某型舰载相控阵雷达有4个天线阵面,每个阵面均由3 000个收发部件组成[2],若采取传统的部件故障后立即停机维修策略,则会使装备停机时间增多,使用可用度下降,即传统单部件事后维修策略很难适用大型相控阵雷达阵面系统,需要研究新的维修策略;二是为提高系统的可测试性、维修性和使用性,大型相控阵雷达天线阵面都进行了机内测试设计[3],具备了状态监控的能力,这为新维修策略的研究提供了机遇。
结合上述维修保障特点,本文提出了一种大型相控阵雷达天线阵面视情维修策略:当机内测试系统监测到天线阵面中故障部件数量达到一定阈值时,雷达停机开始对阵面天线进行换件维修,当天线阵面中故障部件全部更换完毕后,装备重新开始工作。该视情维修策略的优点是简单易执行,并能提前安排维修需要的材料和人员,从而减少了非计划维修产生的停机时间,提高了装备的可用度。
1 视情维修策略
假设大型相控阵雷达天线阵面T/R组件总数为N,为完成规定的预警任务,N个组件中至少需要k个组件正常工作。组件的失效时间都服从参数为λ的指数分布且故障发生相互独立。采用上述视情维修策略对装备进行预防性维修,当天线阵面中故障组件数量达到一定阈值m(m<k)时开始换件维修。装备使用单位有L个维修人员,专门负责更换天线阵面中故障的组件,换件维修时间服从参数为μ的指数分布。装备的运行过程如图1所示。问题在于如何确定最佳的视情维修阈值m和维修人员数量L,使得装备长期运行成本低,效益高。
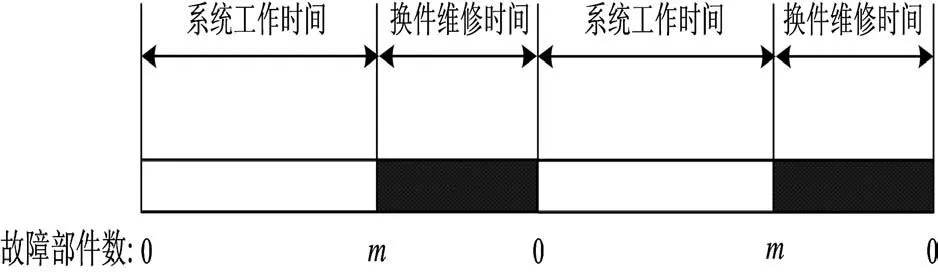
图1 视情维修策略下装备运行过程
2 维修决策优化模型
维修决策模型的核心是研究各种维修策略下的维修目标建模和维修参数优化等决策问题[4]。本文将选取代表装备运行效益和运行成本的使用可用度和平均维修费用率作为优化目标,并对其分析。在此基础上,建立决策模型,优化维修策略。
2.1 使用可用度分析
使用可用度是与能工作时间和不能工作时间有关的一种可用性参数,其度量方法为:系统的工作时间与工作时间、不能工作时间的和之比。结合图1,大型相控阵雷达天线阵面使用可用度A0可以表示为[5]

式中,E(T m)为部件故障数量达到m时天线阵面平均工作时间,E(D)为天线阵面换件维修平均时间。
2.1.1 计算E(T m)
假设X1,X2,…,X N分别为天线阵面中第1个,第2个,第N个组件故障发生的时间,由假设条件可知,X1,X2,…,X N独立同分布,且X1≤X2…≤X N。因此,X1,X2,…,X N符合次序统计量定义,次序统计量X m的生存函数可表示为[6]

式中,R0(x)为组件的可靠度函数,指数分布条件下,R0(x)=e-λ·x。
由E(T m)和X m定义可知,E(T m)等价于第m个故障发生前系统平均工作时间,即[7]

将式(2)代入式(3)中,经化简可得

2.1.2 计算E(D)
维修时间与维修开始时刻天线阵面中故障部件总数有关。在换件维修人员数量为L,换件维修时间服从参数为μ的指数分布的条件下,系统换件维修期望时间E(D)可近似表示为

将式(4)和式(5)代入式(1),即可求出系统使用可用度A0。
2.2 平均维修费用率分析
装备平均维修费用率C是装备单位时间所需的维修费用,主要包括三个部分:一是换件维修所需备件的每小时储存与折旧费Cspare;二是换件维修所需人员的工时费Cperson;三是维修启动费用Cinitialize;平均维修费用率C可表示为
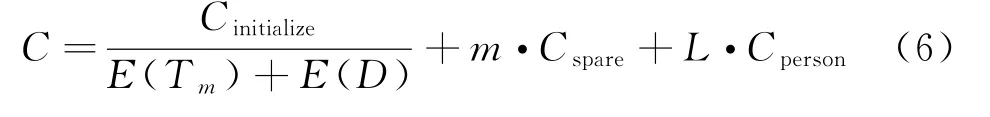
2.3 模型的目标函数
优化模型的目标函数可以是单目标的,如可用度目标、费用目标、风险目标中的一种,也可以是上述单目标的组合,如在某种费用结构限制下,使得装备的使用可用度最大。不同的维修决策目标对维修决策优化结果有较大的影响。由于大型相控阵雷达的运行既要考虑军事效益,也要考虑经济成本,而不能只考虑两者中的一种。因此,本文以系统使用可用度为约束条件,系统期望维修费用率最低为优化目标,建立大型相控阵雷达天线阵面视情维修优化模型。
视情维修优化模型如下所示:
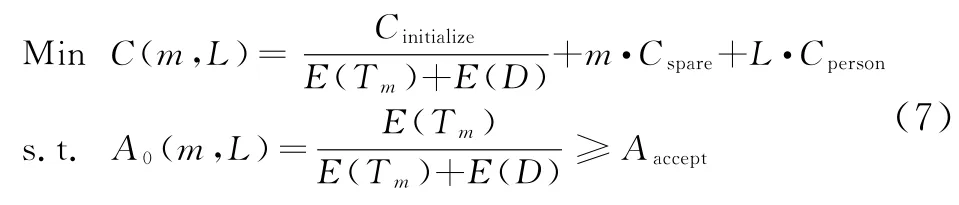
式中,Aaccept为系统最低可接受使用可用度值。
2.4 数值迭代算法
在上述模型中,维修时机(视情维修阈值m)和维修人员数量L时影响维修目标的关键参数。
为求解模型最佳的视情维修阈值moptimal和最佳的换件人数Loptimal,本文给出一种数值迭代的算法,如图2所示。

图2 数值迭代算法流程图
3 实例分析
某大型相控阵雷达天线阵面由3 000个相同的收发组件组成,当阵面组件的总故障数大于300个时,雷达无法完成正常的探测。因此,该天线阵面可视为一个2 700/3000(G)的冗余系统。已知条件有:λ=0.0003次/小时,μ=1个/小时,Cspare=2.5个/小时,Cperson=15人/小时,Cinitialize=50000元,Aaccept=0.95。
图3和图4分别是视情维修阈值m固定时,换件维修人数L对期望维修费用率和使用可用度的影响曲线。

图3 m固定时L对A0的影响曲线

图4 m固定时L对C的影响曲线
由图3和图4可知:当m固定时,L不应过大和过小。L过大时,使用可用度A0虽能满足约束要求,但期望维修费用率C过大;L过小时,期望维修费用率C虽小,但使用可用度A0不能满足约束要求。
图5给出了换件维修人数L固定时,视情维修阈值m对期望维修费用率的影响曲线。
由图5可知:当L固定时,期望维修费用率C随m的递增先下降再缓慢上升,即存在一个最优的(m,L)组合使C最小。
利用数值迭代算法可求出使C(m,L)最小化且满足A0(m,L)>Aaccept的(m,L)组合。最终,得出moptimal=131个,Loptimal=17个,此时使用可用度A0=0.950 76>Aaccept,符合约束条件,而期望维修费用率C达到最小值,C=901.97元/小时。
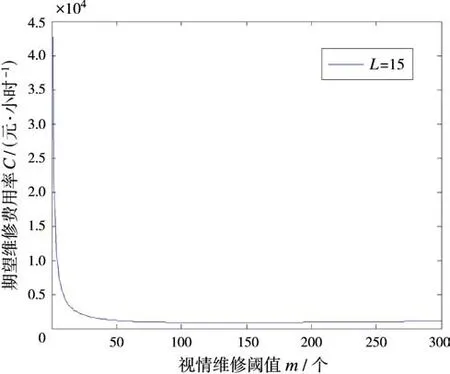
图5 L固定时m对A0的影响曲线
4 结束语
大型相控阵雷达系统组成庞大、结构和工作原理复杂,传统单部件事后维修策略很难适用于大型相控阵雷达阵面系统。本文从大型相控阵雷达维修保障特点出发,提出了一种新的视情维修策略,并以使用可用度维修约束条件,以期望维修费用率最小为目标,建立了视情维修优化模型。该模型可以在保证装备任务可靠性的前提下,对运行成本和运行收益进行综合权衡,并确定最佳的维修时机和维修人数,实现对装备及时、有效、经济的维修。
[1]张光义.空间探测相控阵雷达[M].北京:科学出版社,2001:1-6.
[2]张涛,张建军,郭波.基于使用可用度的k/N系统(m,NG)维修策略分析[J].宇航学报,2009,30(1):395-401.
[3]熊毅,符伟,钱林,等.有源相控阵天线自动测试系统设计[J].雷达科学与技术,2012,10(5):561-564.
[4]左洪福,蔡景.维修决策理论与方法[M].北京:航空工业出版社,2008:7-11.
[5]DE SMIDT-DESTOMBES K S,VAN DER HEIJDEN M C,VAN HARTEN A.On the Availability of a kout-of-N System Given Limited Spares and Repair Capacity under a Condition Based Maintenance Strategy[J].Reliability Engineering and System Safety,2004,83(3):287-300.
[6]ROSS S M.Introduction to Probability Models(10th ed)[M].Singapore:Elsevier Press,2010:45-46.
[7]PHAM H,WANG Hongzhou.Optimal(t,T)Opportunistic Maintenance of a k-out-of-n:G System with Imperfect PM and Partial Failure[J].Naval Research Logistics,2000,47(3):223-239.
——基于教育培训行业的实证分析

