干扰背景下机载雷达广义似然比检测方法
刘维建,常晋聃,李 鸿,谢文冲,王永良
(1.空军预警学院,湖北武汉430019;2.电子信息控制重点实验室,四川成都610036;3.北方电子设备研究所,北京100191)
0 引言
色噪声背景下多通道信号检测问题一直是雷达领域研究的一个重点和难点[1]。由于不存在均匀最大势(UMP,uniformly most powerful)检测器,多种次最优检测器被不断提出。在均匀环境的假设下,根据广义似然比检测器(GLRT,generalized likelihood ratio test)设计原理,Kelly提出了著名的广义似然比检测器(Kelly’s GLRT)[2];在相同的条件下,Robey[3]提出了两步GLRT(2SGLRT,two-step GLRT)检测器,即自适应匹配滤波器(AMF,adaptive matched filter);此外,Rao检测器由De Maio在文献[4]中提出。在部分均匀环境下,Kraut和Scharf提出了自适应相干估计器(ACE,adaptive coherence estimator)[5]。Besson分析了存在一个随机噪声干扰下的自适应检测问题,并提出了GLRT[6],结果表明该检测器与ACE具有相同的形式。该环境下的Rao检测器由Orlando[7]提出,被命名为双归一化自适应匹配滤波器(DN-AMF,double-normalized adaptive matched filter),且被证明与Wald检测器等价[8]。文献[9]假设信号位于某已知子空间中,但信号坐标未知,在此假设下推导了均匀环境中子空间信号的GLRT,结果表明该GLRT是Kelly’s GLRT的推广。
对于机载雷达的工作环境而言,除存在杂波外,往往还存在干扰,而上述检测器均未考虑存在干扰的情况。在实际中,由于敌方的有意干扰或者己方的通信干扰,当采用上述检测器时,往往带来巨大的虚警,使雷达不能正常工作。针对上述问题,本文提出了一步GLRT检测器(1S-GLRT)和两步GLRT检测器(2S-GLRT)。仿真实验验证了新检测器能够有效地抑制干扰,并实现目标检测。
1 问题描述及检测模型
考虑机载雷达空时联合模型。假设阵元数为N a,脉冲数为N b,则系统维数N=N a N b。设待检测单元的接收数据为x。检测问题可用如下的二元假设检验表示:

式中,s,j,n0和n c分别表示信号、干扰、热噪声和杂波。在实际中,不可避免地存在阵元误差、指向误差及多径等因素,这导致信号导向矢量存在失配的现象。而子空间模型是解决信号失配的一个有效途径,为此,s可建模为s=Hθ。实际中,还可能存在多个干扰信号,因此,把j建模为j=Jφ,并假设矩阵H和J张成的子空间不相交。在实际中,可通过空域干扰来向侦测模式或者超分辨空间谱估计算法得到干扰的来向。例如:机载预警雷达中通过在雷达工作间歇插入干扰搜索波束,即利用无源模式侦察到空间各方位的强干扰位置。因此,在本文中,假设矩阵H和J均已知。向量θ和φ分别表示信号和干扰在由矩阵H和J张成的子空间中的坐标。矩阵H和J的维数分别为N×s和N×r,二者均列满秩,并且增广矩阵[H,J]也列满秩,即s+r≤N。令,设杂波加噪声的协方差矩阵为R,即E{n nH}=R。假设有L个独立同分布的训练样本x l,l=1,…,L,且与待检测单元数据具有相同的协方差矩阵,即。假设H和J已知,但φ,θ和R未知。令S=XXH,易知S为L倍的采样协方差矩阵(sample covariance matrix),其中X=[x1,x2,…,x L]是由训练样本组成数据矩阵。
值得注意的是模型(1)具有广泛的适用性,当s=1时,即矩阵H变为列向量,此时对应信号导向向量确知的情况;当s=N时,即矩阵H变为非奇异方阵,此时对应信号导向矢量未知的情况,即位于整个空间中。
2 一步广义似然比检测(1S-GLRT)
1S-GLRT可用如下公式描述[2]:

式中,fτ(x,X)为待检测单元数据x和训练样本数据X在Hτ(τ=0,1)下的联合概率密度函数(PDF,probability density function),γ为满足特定虚警概率(PFA,probability of false alarm)所需的检测门限。
易知,在H1下,x和X的联合PDF为
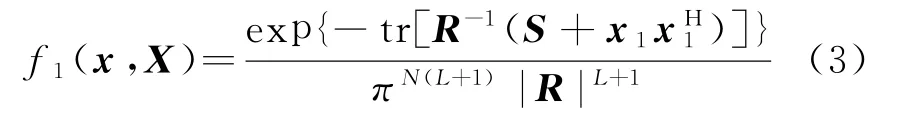
式中,x1=x-Hθ-Jφ。
取式(3)关于R的导数并令其为零,得到R的最大似然估计(MLE,maximum likelihood estimate):
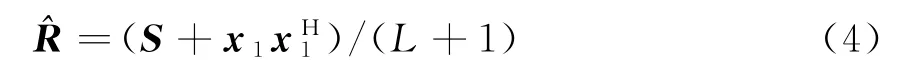
把式(4)代入式(3)得到
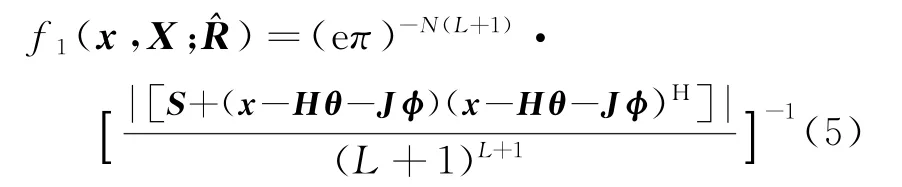
根据矩阵理论得到
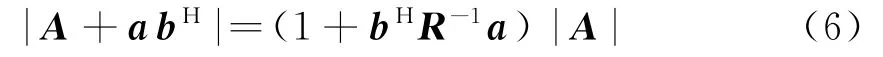
式中,a和b为任意列向量,A为可逆方阵。
利用式(6),式(5)可以等价地表示为
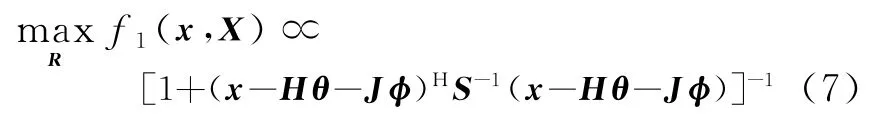
即把θ和φ看作自变量,最大化f1(x,X;),等价于最大化下面函数:
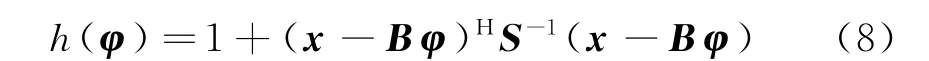
式中,B=[H,J],φ=[θT,φT]T。
取式(8)关于φ的导数并令其为零,得到φ的MLE:
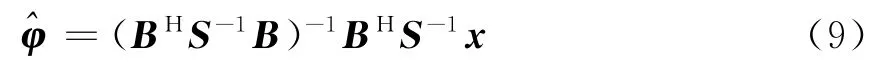
把式(9)代入式(7),经过化简后得到
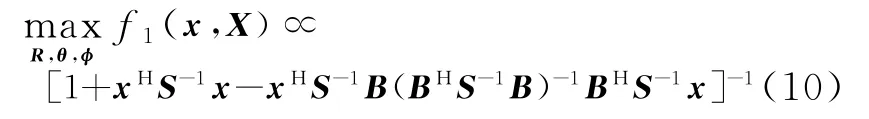
采用相似的方法,可以得到
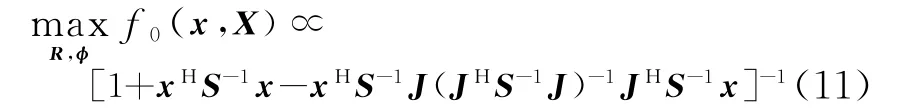
用式(10)除以式(11),得到1S-GLRT为

3 两步广义似然比检测器(2S-GLRT)
2S-GLRT的设计流程如下:先假设协方差矩阵R已知,据此得到GLRT,然后把该结果中的R用采样协方差矩阵代替[3]。
在H1下,待检测单元数据x的PDF为
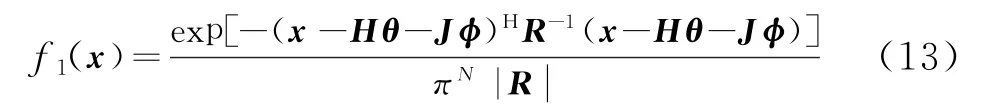
采用与式(9)相同的方法,得到
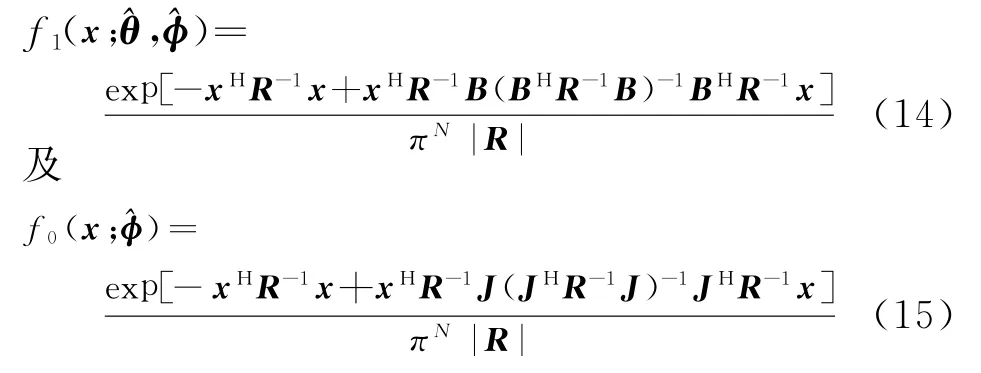
用式(14)除以式(15),并取对数,得到R已知时的似然比检测器:
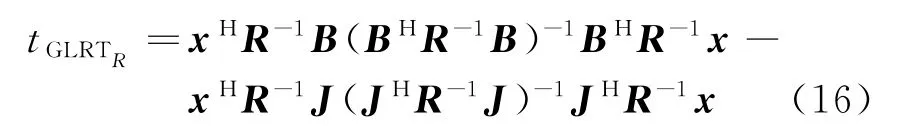
易知,根据训练样本得到的R的M LE为采样协方差/L,其中S如前文所示。把代入式(16)得到2S-GLRT:

4 检测器物理意义分析及恒虚警特性的证明
4.1 1S-GLRT的等价形式及物理意义
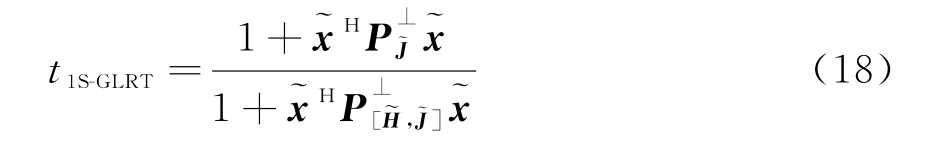
式中,P B表示矩阵B对应的正交投影矩阵;为P B的正交补,即。
根据矩阵正交投影的知识,得到下面的等式[10]:

式中,矩阵A和B具有相同的列。
根据式(19),式(18)可进一步写为
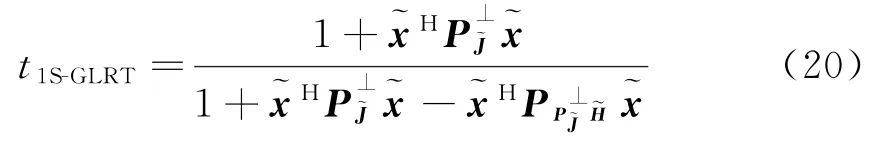
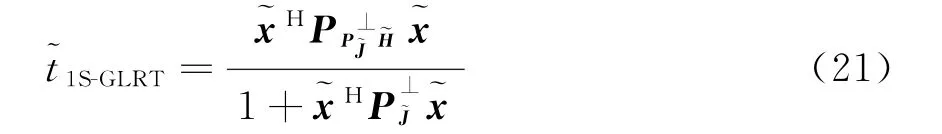

式(22)即为文献[9]中的检测器,当矩阵H的秩为1,即H=s时,式(22)变为

式(23)即为 Kelly’s GLRT[2]。
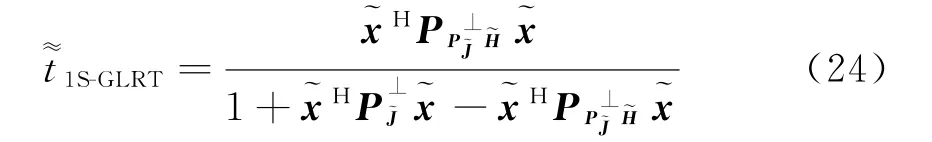
4.2 2S-GLRT的等价形式及物理意义
根据式(19),得到

把式(25)代入式(17)得


当矩阵H的秩为1时,即H=s,式(27)变为

式(28)即为AMF。
比较式(24)和式(26),可得到

另外,式(26)可以写为

即2S-GLRT为能量检测器,检测统计量为预白化后的待检测数据在子空间中的能量。
图1给出1S-GLRT和2S-GLRT的工作流程图。

图1 检测器工作流程图
4.3 1S-GLRT和2S-GLRT的恒虚警特性的证明

易知,在H0下,服从均值为0、自由度为N,协方差矩阵为I N的高斯分布;服从均值为0、自由度为N,协方差矩阵为I N的威沙特(Wishart)分布。因此,t的统计分布均与协方差矩阵R无关。实际上,在H0下,t服从自由度为N和L-N+1的复中心F分布。
此外,根据等式

在 H0下,的统计分布与R无关;同理,在H0下,的统计分布与R无关。因此得出t1S-GLRT和t2S-GLRT均具有CFAR特性。
5 计算机仿真
本文中的1S-GLRT和2S-GLRT的检测概率很难得到解析解,为此我们采用标准的蒙特卡洛(Monte Carlo)仿真对检测器性能进行验证。检测门限和检测概率分别通过100/Pfa和104次蒙特卡洛实验得到。在每次仿真中矩阵H和J随机产生,二者为随机正定Hermitian矩阵的前s列和后r列。φ取为零均值复高斯随机向量,其协方差矩阵为,其中为单个干扰的功率。令,其中为零均值复高斯随机向量,其协方差矩阵为I s,a为复标量,其相位在[0,2π]上均匀分布。
信杂噪比(SCNR,signal-to-clutter-plus-noise ratio)定义为
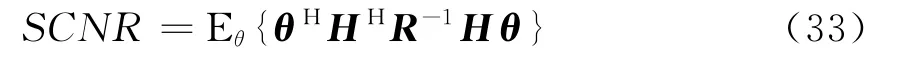
根据θ的统计特性,式(33)可以表示为
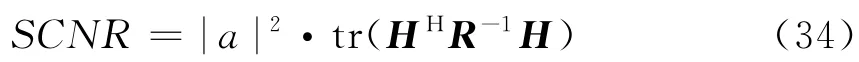
为计算方便,假定高斯热噪声的功率为1,即杂波加噪声的协方差矩阵可以表示为R=I+Rc,其中Rc为杂波的协方差矩阵,单位阵I为热噪声的协方差矩阵。相应地,干噪比(JNR,jamming-to-noise ratio)可以被定义为

图2给出不同SCNR下四种信号子空间维数和干扰子空间维数对应的1S-GLRT和2S-GLRT的检测概率。其中N a=3,N p=4,训练样本数为L=2N,杂噪比(CNR,clutter-to-noise ratio)为60 dB,JNR=15 dB,PFA为10-3。从图中可以看出,随着SCNR的增加,1S-GLRT和2S-GLRT的检测概率均不断提高;1S-GLRT的检测概率比2S-GLRT的略高,但当SCNR很大时,二者的检测概率基本相同。
图3给出不同训练样本数目下四种信号子空间维数和干扰子空间维数对应的1S-GLRT和2S-GLRT的检测概率。其中,SCNR=30 d B,JNR=15 dB,其他参数和图2相同。从图中可以看出,随着训练样本数的增加,检测概率不断提高。1S-GLRT的检测概率比2S-GLRT的略高,这与图2中的结果相同。
图4给出了不同JNR下四种信号子空间维数和干扰子空间维数对应的1S-GLRT和2S-GLRT的检测概率。其中,SCNR=30 dB,L=2N,其他参数和图2相同。从图中可以看出,JNR对两种检测器的检测概率基本没有影响。其实,这从1S-GLRT和2S-GLRT的表达式中可以看出:检测器利用了干扰子空间信息,而没用到干扰的功率信息。另外,可以看出,1S-GLRT的检测概率和2S-GLRT的检测概率基本相同。
图5给出了不同信号子空间和干扰子空间维数下,1S-GLRT和2S-GLRT的检测性能。其中,SCNR=30 d B,JNR=15 d B,L=2N,其他参数和图2相同。从图中可以看出,随着干扰子空间维数从1增加到N,1S-GLRT和2S-GLRT的检测概率均从1逐渐下降到0。值得指出的是,当干扰子空间的维数为r0时,信号子空间的维数最大为N-r0。另外,需要指出的是,在相同的干扰子空间维数下,信号对检测器的影响主要体现在信号能量(即SCNR),而非信号子空间的维数。
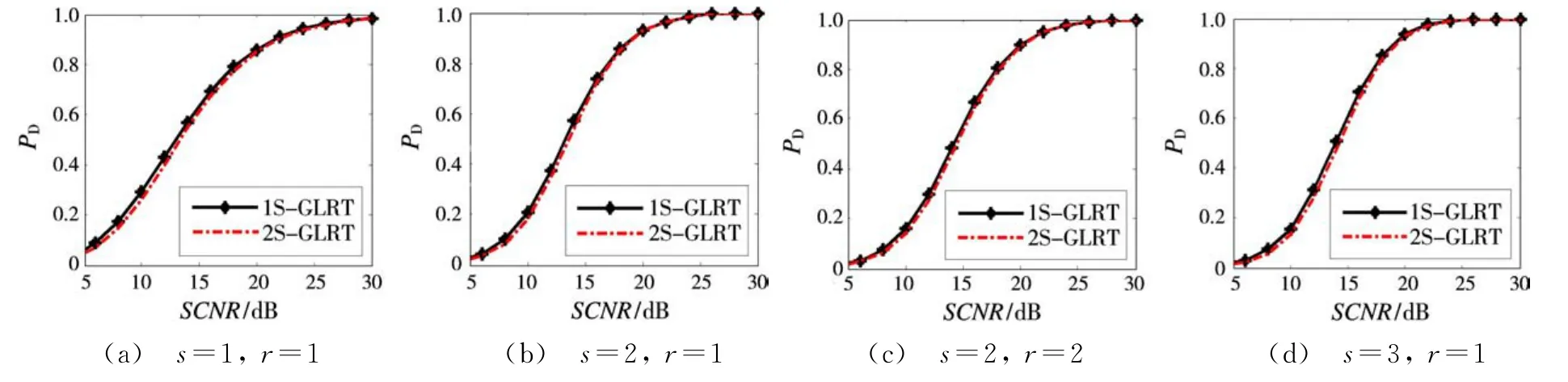
图2 不同SCNR下1S-GLRT和2S-GLRT检测性能比较

图3 不同训练样本数下1S-GLRT和2S-GLRT检测性能比较
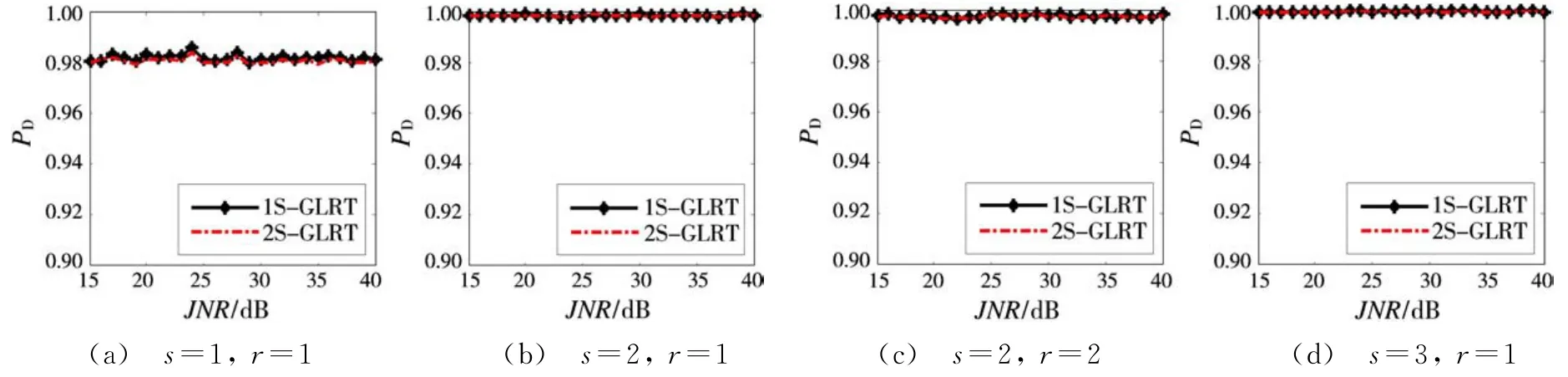
图4 不同JNR下1S-GLRT和2S-GLRT检测性能比较

图5 不同信号子空间维数和干扰子空间维数下1S-GLRT和2S-GLRT检测性能
6 结束语
本文提出了干扰背景下适用于机载雷达环境的1S-GLRT和2S-GLRT两种检测器。1S-GLRT和2S-GLRT均具有CFAR特性;1S-GLRT比2SGLRT具有略高的检测概率,但当SCNR较高时,二者的检测概率基本相同。与1S-GLRT相比,2SGLRT更容易实现。随着SCNR和训练样本数的增加,1S-GLRT和2S-GLRT的检测概率均会增加;两种检测器均不受干扰功率的影响。另外,本文提出的1S-GLRT是多阶GLRT和Kelly’s GLRT的推广,2S-GLRT是AMF的推广。
[1]康连瑞,金伟,刘向阳.K杂波下基于Bootstrap的分布式检测[J].雷达科学与技术,2012,10(2):187-191.KANG Lian-rui,JIN Wei,LIU Xiang-yang.Bootstrap Based Distributed Detector Under Correlated K-Distributed Radar Clutter Background[J].Radar Science and Technology,2012,10(2):187-191.(in Chinese)
[2]KELLY E J.An Adaptive Detection Algorithm[J].IEEE Trans on Aerospace and Electronic Systems,1986,22(2):115-127.
[3]ROBEY F C,FUHRMANN D R,KELLY E J,et al.A CFAR Adaptive Matched Filter Detector[J].IEEE Trans on Aerospace and Electronic Systems,1992,28(1):208-216.
[4]DE MAIO A.Rao Test for Adaptive Detection in Gaussian Interference with Unknown Covariance Matrix[J].IEEE Trans on Signal Processing,2007,55(7):3577-3584.
[5]KRAUT S,SCHARF L L.The CFAR Adaptive Subspace Detector is a Scale-Invariant GLRT[J].IEEE Trans on Signal Processing,1999,47(9):2538-2541.
[6]BESSON O.Detection in the Presence of Surprise or Undernulled Interference[J].IEEE Signal Processing Letters,2007,14(5):352-354.
[7]ORLANDO D,RICCI G.A Rao Test with Enhanced Selectivity Properties in Homogeneous Scenarios[J].IEEE Trans on Signal Processing,2010,58(10):5385-5390.
[8]LIU W,XIE W,WANG Y.A Wald Test with Enhanced Selectivity Properties in Homogeneous Environments[J].EURASIP Journal on Advances in Signal Processing,2013,2013(14):1-4.
[9]RAGHAVAN R S.Performance of the GLRT for Adaptive Vector Subspace Detection[J].IEEE Trans on Aerospace and Electronic Systems,1996,32(4):1473-1487.
[10]YANAI H,TAKEUCHI K,TAKANE Y.Projection Matrices,Generalized Inverse Matrices,and Singular Value Decomposition[M].New York:Springer,2011.

