凸模糊映射的几种定义及其性质
何 豆
(重庆师范大学数学学院 重庆 401331)
凸模糊映射的几种定义及其性质
何 豆
(重庆师范大学数学学院 重庆 401331)
在已有文献的基础上,介绍了几种常见的凸模糊映射的定义,同时,给出了在可微条件下凸模糊映射的一些性质。并得到了凸模糊映射的等价刻画。
凸模糊映射;可微凸模糊映射;下半连续;上半连续
一、预备知识
随着模糊凸集研究的深入与发展,许多学者讨论了模糊映射在模糊凸集上的凸性及其在模糊规划中的应用。凸模糊映射是模糊规划中的重要内容,因此,有必要进一步讨论模糊映射在凸集上的凸性及其性质。本文主要从以下几个方面展开,介绍了不同条件下凸模糊映射的定义,分析了其相关性质,给出了可微条件下凸模糊映射的等价刻画。凸模糊映射的几种定义:
1.1992年Nanda和Kar[1],在引入区间数的定义及运算法则之后,建立了由矢量空间到模糊数之间的映射,在此基础上给出了凸模糊映射的如下定义:
定义1[1]设为矢量空间中的一个非空凸集,F∶C→E1为模糊映射,如果对任意的,有

则称F为C上的凸模糊映射。
特别的,定义在凸集上的凸模糊映射是凸的当且仅当它的上图是凸的。
2.1998年Nagata[2]将凸性和局部利普西兹连续两个概念F(引ax入+到(1-模糊映射,通过规定模糊数的模糊最大顺序:

给出了凸模糊映射的定义和局部利普西兹连续模糊映射的定义,同时也给出了模糊映射的局部利普西兹连续的基本定理。其中凸模糊映射的定义如下:
定义2[2]设Ω为Rn中的一个非空凸集,F:Ω→E1为模糊映射,如果对于任意的x, y∈Ω,及0≤a≤1,有F(αx+(1-α)y≤αFx)+(1-α) F(y),则称F为Ω上的凸模糊映射。
3.2002年, Hong和Xu在Goetschel和Voxman所给出的包含模糊数空间E1的空间

给出了模糊映射F:Ω→E1为凸的如下定义:
定义3 设Ω为Rn中的一个非空凸集,F:Ω→E1为模糊映射,如果对于任意的x, y∈Ω,及0≤l≤1,有,即

则称F为Ω上的凸模糊映射。
定义4 设Ω为Rn中的一个非空凸集,F:Ω→E1为模糊映射,如果对于都是Ω上的凸函数,即对于有

则称F为Ω上的凸模糊映射。
注:关于凸模糊映射的上述定义中,最常用且用起来最方便的还是定义4
定义5 设F: C→E1为模糊映射且x0∈C,若对任给的e>0,都存在d>0使得当x∈C且时
1.如果F( x0)≤F( x)+e,则称F在点x0处是下半连续。如果F在C上的每一点处都是下半连续,则称F在C上是下半连续的。
2.如果F( x)≤F( x0)+e ,则称F在点x0处是上半连续。如果F在C上的每一点处都是上半连续,则称F在C上是上半连续的。
引理1 设F: C→E1为模糊映射,如果存在a∈(0,1),使得对任意的x, y∈C,都有则集
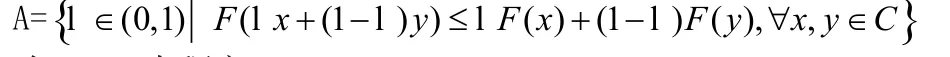
在[0,1]中稠密。
二、主要结论
凸模糊映射的性质。定理1:设F: C→E1为下半连续模糊映射,如果存在a∈(0,1),使得对任意的x, y∈C,都有则称F是C上的凸模糊映射。

所以由F的下半连续性,对任给的e>0,存在N>0,使得当n>N时有

于是由ln∈A有,因此对任意的r∈[0,1]有

于是由ε的任意性,令n→∞则对任意的r∈[0,1]有

因此对任意的x, y∈C有

即F是C上的凸模糊映射。
定理2:设F: C→E1为上半连续模糊映射,如果存在a∈(0,1),使得对任意的x, y∈C,都有则称 是 上的凸模糊映射。
定理3:设C是闭集且F: C→E1为下半连续模糊映射,如果对任意的x, y∈C,都存在l∈(0,1)( λ取决于x,y)使得

则称F是C上的凸模糊映射。
证明:设F: C→E1为下半连续模糊映射,则对任意的都是 上的下半连续实值函数,从而是Rn+1中的闭集。
O159.2
A
1000-9795(2014)08-000224-02
何 豆(1989-),女,陕西兴平人,硕士研究生,专业:运筹学与控制论,研究方向:优化理论与算法。

