环境作用动力学及其在武器装备定寿延寿中的应用
封先河,曹学军,杨万均,朱蕾,杨晓然,魏小琴
(1.西南技术工程研究所,重庆400039;2.兵科院宁波分院,浙江宁波315103)
环境作用动力学及其在武器装备定寿延寿中的应用
封先河1,曹学军2,杨万均1,朱蕾1,杨晓然1,魏小琴1
(1.西南技术工程研究所,重庆400039;2.兵科院宁波分院,浙江宁波315103)
目的研究环境作用动力学及其在武器装备定寿延寿中的应用。方法修正蠕变动力学并提出环境作用动力学,应用环境作用动力学,先期获得武器装备材料和零部件的老化、损伤函数通解,通过短暂的自然环境试验和加速试验数据,确定老化、损伤函数通解的待定系数,外推完成武器装备定寿延寿。结果提出了环境作用动力学,并应用于尾翼弹簧和压缩橡胶密封圈的寿命评估。结论环境作用动力学可以广泛应用于武器装备材料、零部件的定寿延寿领域,为整机、整弹的定寿延寿提供基础支撑。
环境作用动力学;定寿;延寿;老化;蠕变
武器装备由大量高性能的材料和零部件组成。在武器装备定寿延寿中,描述这些材料和零部件的老化、损伤过程,掌握材料和零部件的老化、损伤规律,是武器装备定寿延寿的基础。
获得材料和零部件的老化、损伤规律,一般通过试验手段。试验分为自然环境试验和实验室加速试验,自然环境试验周期长,在武器装备定寿延寿中的应用较少;实验室加速试验周期短,但必须保证实验室加速试验和实际环境存在相同的老化、损伤机理,这在老化、损伤机理尚不明确的条件下难以满足。如果能够通过经验公式和理论模型先期获得武器装备材料和零部件的老化、损伤函数,通过短暂的自然环境试验数据,确定老化、损伤函数的待定系数,即可外推完成武器装备的定寿延寿工作。
目前,可用的经验公式和理论模型,包括化学动力学理论[1]、粘弹性理论[2]、催化理论等,也包括一些经验公式,如著名的阿伦尼乌斯公式及其各种修正形式[3—7],还包括一些新建立的模型[8—15]。
这些经验公式和理论模型,一般只能应用于单独具体的物理变化、化学变化或特定的变化过程,缺乏普适性。在处理既有物理变化又有化学变化的复杂变化过程中,所得结果不可靠。这些经验公式和理论模型,缺乏合理的外推依据,外推稳定性普遍较差。
笔者认为:武器装备材料和零部件的老化、损伤过程,可以用经蠕变动力学[16—17]作适当修正的环境作用动力学求得老化、损伤函数通解,通过短暂的自然环境试验和加速试验数据,确定老化、损伤函数通解的待定系数,外推完成武器装备定寿延寿工作。
依据上述观点,近几年应用环境作用动力学进行了几个武器装备的定寿延寿工作,取得了一定的应用效果,可以应用于武器装备材料、零部件的定寿延寿领域,为整机、整弹的定寿延寿提供基础支撑。
1 环境作用动力学
环境作用动力学假设物质由大量粒子组成,是孤立的平衡系统。这些粒子包括无机或有机材料的分子、金属材料的单原子分子、晶体材料的晶格等。每个粒子存在变化和未变化两个状态。按照统计物理的等几率原理,粒子的微观状态满足最可几分布[18]。
在物质宏观的形态和性质的变化过程中,只有很少一部分粒子能够产生变化,且不是都同时、均匀产生变化。产生变化的粒子能级εn高于某个特征能量值Ep,Ep代表粒子间相互作用的大小。
定义1:能级εn高于某个特征能量值Ep的粒子称为活化粒子。
假设1:组成物质的所有粒子中,能够产生物理化学变化的活化粒子的特征能量值Ep,由与温度无关的E0和与温度有关的EvT两部分组成。
可以用一个函数来描述与温度有关的EvT,函数的自变量为热力学温度,它与组成物质的粒子间的相互作用有关,可以通过实验数据确定。作为一个近似的估计,EvT可以用温度的二次函数表示。即:

式中:g,f为常数;T为热力学温度;Ep为特征能量值;E0为Ep中与温度无关的部分;EvT为Ep中与温度有关的部分。
定义2:组成物质的所有粒子中,活化粒子数N0占总粒子数N的比,称为物质的活化粒子浓度W(T)。即:

活化粒子浓度与温度有关,可以通过统计物理进行计算。(3)式可以近似表示固体、液体、气体的活化粒子浓度W:

将(1)式代入(3)式有:

定义3:组成物质的所有粒子中,已经发生变化的粒子数占所有粒子数的比,称为物质的变化进程。简称变化进程P,是一个0~1之间的无量纲数。
所有粒子都未发生变化时,变化进程P=0;所有粒子都发生变化时,变化进程P=1;部分粒子发生变化时,变化进程P在0和1之间。
变化进程P的重要性在于相同活化粒子浓度可能具有不同的变化速度。因为随着变化的进行,活化粒子中有一部分已经产生了变化,这些粒子对变化速率是没有贡献的,只有未产生变化的活化粒子,才对变化速度产生影响。
变化进程P是一个微观量,难以测量,一个具体的物理化学变化过程,只能用一个宏观的物理量来描述变化进行的过程,这个物理量必须与变化进程P相对应。
定义4:组成物质的所有粒子中,与变化进程P成线性对应关系的宏观物理量,称为物质的变化度量值。简称变化度量值I,即:

式中:C,K为常数。在物质的所有物理、化学变化过程中,不同的环境作用会产生不同的变化规律。
定义5:在物质的所有宏观物理、化学变化过程中,影响变化过程独立、有效的作用的积,称为环境作用σ。包括表面挥发作用、外部应力作用、内部扩散、内部质量作用等。即:

这里的环境作用包括物体内部和外部的环境作用,不仅仅局限于物体外部的环境作用。环境作用σ可以是时间和温度的函数,也可以是恒定的常数,还可以随变化度量值I或变化进程P变化。
假设2:在物质的所有宏观物理、化学变化过程中,物质的变化进程P对对数时间t的导数,与环境作用σ和活化粒子中未发生变化部分浓度的积成正比。即:

式中:σ为环境作用;j为比例系数,同时平衡量纲;P为变化进程;W为活化粒子浓度。可以用变化度量值I表示,代入(5)式有:

2 环境作用动力学在武器装备定寿延寿中的应用
环境作用动力学方程是一个以时间为变量的常微分方程,描述的是物质宏观形态和性质随时间的变化规律,其应用对象为由大量微观粒子组成的物质,涉及物理、化学等领域。
应用环境作用动力学方程,必须确定两个重要关系:一个是t=0的初始条件;另一个是变化进程和变化度量值的关系,它是微观量与宏观性质联系的桥梁。
环境作用动力学的应用难点,在于环境作用的定量描述。各种纷繁复杂的物质宏观变化过程,除了组成物质粒子不同的内部原因外,不同环境作用的外部原因,增加了物质宏观变化的复杂性。
下面列举几个例子,说明环境作用动力学的应用。
2.1 弹翼张开簧的储存寿命评估
2.1.1试验过程
某型导弹弹翼张开簧储存过程中被压缩至22 mm,原始自由长度为59 mm,储存温度为25℃,评估其储存11年后,自由长度是否大于51 mm。试验示意如图1所示。

图1 弹簧储存寿命评估示意Fig.1 Sketch map of spring storage life valuation
根据环境作用动力学定义4,张开簧压缩比为变化度量值I,即:

式中:H0为弹翼张开簧原始自由长度;I(t,T)为变化度量值;H为压缩时间t后,张开簧的自由长度。
试验方案:选 4个试验温度水平进行试验(140,110,80,50℃),重复取样13次,2个平行样,每一个试样按照(9)式计算其变化度量值,每一次取样的变化度量值为2个平行样的平均值,取样时间由(10)式确定:

式中:n为取样次数;t为取样时间,min。
用50℃试验结果进行外推检验,140,110,80℃的试验结果确定通解系数。试验结果如图2所示,纵坐标为蠕变度量值,横坐标为对数时间ln(t+1)。

图2 试验结果Fig.2 Result of experiment
2.1.2试验分析
压缩发生前,自由长度为H0,张开簧的变化进程P为0,变化度量值I为1;压缩结束时,自由长度为h,变化进程P为1,变化度量值I为h/H0。于是有:

张开簧的环境作用σ为压缩变形量h/H0减去变化度量值,随着自由长度的变化,环境作用σ也是变化的,逐步减小直到趋于0。即:

比较式(11)和环境作用动力学式(5),可以确定K,C,应用环境作用动力学(8)式得微分方程:

这是一个黎卡提(Riccati)方程[19],作适当变换后得通解:

注意到t→∞时,I(t,T)=h/H0,t=0时,I(t,T)= 1,于是常数C=h/(H0-h),j=1,代入(14)有:

由140,110,80℃的试验结果确定方程(15)的三个系数E0,f和g,得如下函数:

式中:t为时间;T为热力学温度。
由此函数计算50℃的计算值,与50℃的试验结果进行比较,结果如图3所示。

图3 计算值与试验值比较Fig.3 Comparison of calculation value and experiment value
外推检验结果:(16)式达到了很高的精度,对50℃的试验数据最大误差小于1%,外推稳定。
应用(16)式计算25℃环境条件下储存11年的变化度量值,再由(9)式可以转换为11年的自由长度H11:

评估结论:该弹翼张开簧在25℃环境条件下储存寿命大于11年。
2.2 橡胶密封圈储存寿命评估
某导弹发动机的O形橡胶密封圈,在25℃环境条件下储存,储存时受压力和温度等环境作用,橡胶密封圈产生永久变形,其压缩比减少,密封性能下降,引起泄漏,导致整个导弹系统故障。只要压缩比大于80%,就可以确保其密封性能。橡胶密封圈储存寿命评估的目的,是评估导弹储存多少年后,橡胶密封圈压缩比大于80%。
2.2.1热失重试验
首先测定橡胶密封圈热失重,温度点选择125, 150,175,200℃等5个。试验结果如图4所示。
2.2.2老化试验
原始高度为H0的橡胶密封圈,在夹具中压缩到固定高度h,在环境温度为T的条件下贮存,经过时间t后,从夹具取出,用橡胶测厚计测量其的自由高度H,每一个试样按照(18)式变化度量值。如图5所示。
根据环境作用动力学定义4,橡胶密封圈永久压缩比为变化度量值I,即:

图4 橡胶密封圈热失重Fig.4 Thermal weight loss of rubber seals

图5 橡胶密封圈老化试验示意Fig.5 Sketch map of aging experiment of rubber seals

试验温度为:常温,100,125,150,175,200℃,共6个。每测试点3个平行样。原始平均高度H0为3.956 mm,压缩的平均高度为3 mm,结果如图6所示。

图6 橡胶密封圈老化试验结果Fig.6 Aging experiment result of the rubber seals
2.2.3试验分析
首先分析热失重试验。由数据可见,质量损失率与时间呈现出过原点的线性关系,满足(19)式,称为挥发作用:

分析老化试验得,压缩变形发生前,自由高度为H0,变化进程为0,变化度量值为1;结束时,自由高度为h,变化进程为1,变化度量值为h/H0。于是有:
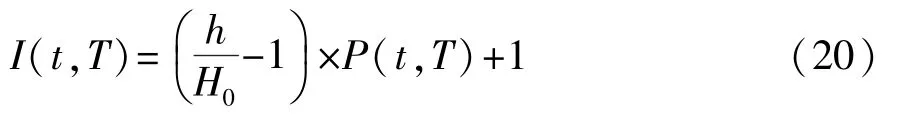
橡胶密封圈的压缩作用Z为:压缩变形量h/H0减去变化度量值I。随自由长度的变化,Z也是变化的。即:

橡胶密封圈的挥发作用和压缩作用为两个独立的作用,根据环境作用动力学定义5,橡胶密封圈存在的环境作用为:

应用环境作用动力学方程(8)有:

考虑到t>>1时,t/(1+t)≈1,式(23)简化为:

得通解:

(25)式中,j取1,并代入h,H0,H的值。用全局最优化算法,由100,125,150,175,200℃的试验数据,以及常温下273天以内的试验数据,确定通解(25)式的3个待定常数E0,f,g。得:

用常温下273天到1278天的试验数据,检验(26)式,得如图7所示结果。
每个测试点的绝对值平均误差为1.108%,最大误差为2.27%,外推稳定。
应用(26)式计算25℃环境条件下压缩比大于80%的储存年限为:

图7 常温试验数据与计算数据比较Fig.7 Comparison of normal temperature experiments data and calculation data

评估结论:该橡胶密封圈在25℃,压缩平均高度为3 mm的存储环境条件下,压缩比大于80%的储存年限为12.5年。
3 结语
环境作用动力学用一个常微分方程,将宏观物质形态和性质的变化与环境作用、热力学温度和时间联系起来。适用于由大量微观粒子组成的物质的物理化学变化过程,具备高度的概括能力和简单易用性,应用领域广泛。
环境作用动力学应用在武器装备定寿延寿中,具有得天独厚的优越性。环境作用动力学可以确定武器装备材料和零部件的变化规律通解,材料和零部件的短期试验数据包含了其自身特征性能,依据实际这些短期试验数据,修正其变化规律通解的待定系数,所得的具体变化规律与实际情况十分吻合,可以在较大温度范围和较长时间范围内准确描述武器装备材料和零部件的变化规律。
从目前的应用情况来看,环境作用动力学在弹簧蠕变和橡胶密封圈老化方面,表现出良好的准确性和外推能力,更加广泛的应用正在进行中。
致谢:感谢国防科技环境试验研究中心及中国兵器工业第五九研究所的领导和同事们的支持和帮助!
[1] PETER A,JULIO D P.Atkins'Physical Chemical[M]. Beijing:Higher Education Press,2009:813—1013.
[2] FINDLEY W N,LAI J S,ONARAN K.Creep and Relaxation of Nonlinear Viscoelastic Materials[M].NewYork: Holland Publishing Co,Amsternam,1977.
[3] LANGER J S,ANAËL Lemaître.Dynamic Model of Super -Arrhenius Relaxation Rates in Glassy Materials[J]. Physical Review Letters,2005,94(6):175701—1.
[4] GALWEY K Andrew,BROWN E Michael.APPlication of the Arrhenius Equation to Solid State Kinetics:Can This be Justifid[J].Thermochimica Acta,2002(286):91—98. [5] GALWEY AK,BROWN ME.APPlication of the Arrhenius Equation to Solid State Kinetics:Can This Be Justifid? [J].Thermochimica Acta,2002(286):91—98.
[6] 王登霞,李晖,孙岩,等.HNBR自然老化规律及储存寿命预测研究[J].装备环境工程,2013,10(6):23—28. WANG Deng-xia,LI Hui,SUN Yan,et al.Weather Aging of HNBR and Its Storage Life Prediction[J].Equipment Environmental Engineering,2013,10(6):23—28.
[7] 孙伟星,刘山尖,欧阳昕,等.橡胶隔振器寿命预测及加速试验研究进展[J].装备环境工程,2013,10(1): 57—60. SUN Wei-xing,LIU Shan-jian,OU-YANG Xin,et al.Advances in Fatigue Life Prediction and Accelerated Test of Rubber Vibration Isolator[J].Equipment Environmental Engineering.2013,10(1):57—60.
[8] 陈宏善,侯婷婷,冯养平.聚合物物理老化的分数阶模型[J].中国科学:物理学、力学、天文学,2010,40 (10):1267—1274. CHEN Hong-shan,HOU Ting-ting,FENG Yang-ping.Polymer Physics Aging Score Rank Model[J].Scientia Sinica(Physica Mechanica&Astronomica),2010,40(10): 1267—1274.
[9] DUSAN K,ANTONIO R.Thermodynamics and Statistical Physics of Damage Processes in Quasi-ductile Solids[J]. Mechanics of Materials,2005(37):299—315.
[10]HANI M H,FRANCISCO O,RAMÓN G R,et al.Longtime Relaxation Dynamics of Langmuir Films of a Glass-Forming Polymer:Evidence of Glasslike Dynamics in Two Dimensions[J].Physical Review Letters,2004,92(25): 255503—1.
[11]GREENFIELD P.Creep of Metals at High Temperature [M].London:Mills&Boon Ltd,1972.
[12]HOÁNG M E,LOWE David.Lifetime Prediction of a Blue PE100 Water Pipe[J].Polymer Degradation and Stability,2008,93:1496—1503.
[13]JUNGIN K,WOO Il L,STEPHEN W T.Modeling of Mechanical Property Degradation by Short-term Aging at High Temperatures[J].Composites:Part B,2002(33): 531—543.
[14]DUSAN K,ANTONIO R.Thermodynamics and Statistical Physics of Damage Processes in Quasi-ductile Solids[J]. Mechanics of Materials,2005(37):299—315.
[15]VALANIS K C,PENG S T J.Deformation Kinetics of Ageing Materials[J].Polymer,1983,24:1551—1557.
[16]封先河.蠕变动力学模型及其在弹簧蠕变中的应用[J].科学通报,2012,57(25):2354—2358. FENG Xian-he.Creep Dynamic Model and Its Application to the Creep of Spring[J].Chinese Science Bulletin, 2012,57(25):2354—2358.
[17]封先河,魏小琴.压缩橡胶密封圈蠕变/老化行为研究[J].中国科学:物理学、力学、天文学,2014,44(5): 486—491. FENG Xian-he,WEI Xiao-qin.Creep/Aging Behavior Study of Compressed Fluorinated Silicone Rubber Oring [J].Scientia Sinica(Physica Mechanica&Astronomica),2014,44(5):486—491.
[18]汪志诚.热力学 统计物理[M].北京:高等教育出版社,1980. WANG Zhi-cheng.ThermodynamicsStatisticsPhysics [M].Beijing:Higher Education Publisher,1980.
[19]任永泰,史希福.常微分方程[M].沈阳:辽宁人民出版社,1984. REN Yun-tai,SHI Xi-fu.Ordinary Differential Equation [M].Shenyang:People's Publisher in Liaoning,1984.
Dynamics of Environmental Effect and Its Application in Determination and Extension of Weapon Service Life
FENG Xian-he1,CAO Xue-jun2,YANG Wan-jun1,ZHU Lei1,YANG Xiao-ran1,WEI Xiao-qin1
(1.Southwest Technology and Engineering Research Institute,Chongqing 400039,China; 2.Weapon Science Institute,Ningbo 315103,China)
ObjectiveTo put forward the theory of dynamics of environmental effect and its application in determination and extension of weapon service life.MethodsDynamics of environmental effect was modified from creep dynamics;common solutions of weathering and damage function of the military material and parts were obtained using dynamics of environmental effect;the parameters of the common solutions were determined using short-term natural environmental test and accelerated test;the weapon service life was determined and extended by extrapolation.ResultsThe theory of dynamics of environmental effect was proposed;the theory was applied in service life evaluation of empennage spring and pressed rubber seal ring.ConclusionThe theory of dynamics of environmental effect can be widely applied in determination and extension of service life of weapon material and parts,and provides basic support for the determination and extension of service life of the whole equipment or ammunitiont.
dynamics of environmental effect;life determination;life extension;ageing;creep
10.7643/issn.1672-9242.2014.04.006
TJ760
:A
1672-9242(2014)04-0026-06
2014-05-29;
2014-06-19
Received:2014-05-29;Revised:2014-06-19
封先河(1967—),男,重庆人,研究员级高级工程师,主要研究方向为环境试验及理论。
Biography:FENG Xian-he(1967—),Male,from Chongqing,Researcher level senior engineer,Research focus:environmental test and theory.

