2A12铝合金微动疲劳全寿命预测方法研究

陈跃良,徐丽,2,张勇,刘旭

(1.海军航空工程学院青岛校区,山东青岛266041;2.海军航空兵学院,辽宁葫芦岛125001)

专题——武器装备定寿与延寿技术

2A12铝合金微动疲劳全寿命预测方法研究

陈跃良1,徐丽1,2,张勇1,刘旭1

(1.海军航空工程学院青岛校区,山东青岛266041;2.海军航空兵学院,辽宁葫芦岛125001)

目的对于2A12铝合金,提出基于成核寿命和扩展寿命的微动疲劳全寿命预测方法。方法基于损伤力学法计算裂纹成核寿命,利用扩展有限元计算裂纹尖端应力强度因子,应用断裂力学计算裂纹扩展寿命,并对预测者和试验值进行比较。结果损伤力学法能考虑接触面应力三维度的作用来反映多轴状态作用,能有效模拟微动疲劳多轴行为。基于损伤力学法的微动疲劳全寿命预测模型能有效预测微动疲劳全寿命。由于微动作用,裂纹成核非常早,扩展寿命从试件的近表面开始,占全寿命的主要部分。结论考虑成核寿命和扩展寿命的微动疲劳全寿命分析是完善的,预测值与试验值比较吻合。

2A12铝合金;损伤力学法;微动疲劳;全寿命

关于微动疲劳寿命的研究,目前应用较多的方法主要有:局部应力-应变法、名义应力法、断裂力学法、基于临界面的疲劳参数法以及基于损伤力学法的微动疲劳寿命预测方法[1—4]。

微动疲劳寿命是裂纹成核寿命和扩展寿命的总和,但在寿命预测中往往只考虑成核寿命或只考虑扩展寿命。文献[5—7]基于断裂力学进行微动疲劳扩展寿命预测,研究发现裂纹扩展寿命占全寿命的主要部分,然而,Hill[8]和Szolwinski[9]等其他研究者支持微动疲劳是一个成核控制的过程这一论点,认为微动疲劳成核寿命占全寿命的主导部分。产生这一矛盾的主要原因与材料本身的特性和初始裂纹的选取有关。近年来,Houghton和Wavish[10]又提出了微动疲劳全寿命预测方法,其基本原理是用多轴疲劳参数计算裂纹成核寿命,用线弹性断裂力学计算裂纹扩展寿命,并考虑短裂纹作用进行修正。

对于2A12铝合金,文中提出了基于损伤力学和断裂力学的微动疲劳全寿命预测方法,利用扩展有限元计算应力强度因子,结合全寿命预测模型计算微动疲劳寿命,并分析了裂纹成核寿命、扩展寿命比例。

1 成核寿命计算

材料损伤主要是微裂纹和夹杂成核及扩展累积的过程。Kachanov[11]首先引入损伤变量,考虑应力应变建立本构方程来预测裂纹成核。

损耗势能函数φ为损伤弹性能释放率Y、塑性应变率˙P、累积微塑性应变˙π等3个主要变量的函数,根据热力学可表示为[12]:

式中:C和β为材料常数;Y为与损伤参数D有关的热力学变量,根据热力学势函数(ψ)可表示为:

式中:ρ为密度;E为弹性模量;σ*为等效多轴损伤应力。用Von Mises等效应力σeq和三维函数Rv表示为:

式中Rv可表示为:

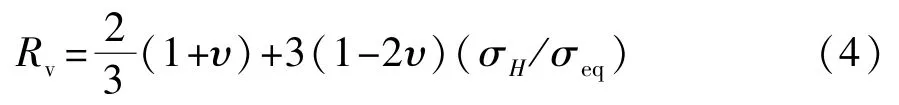
式中:σH为静水应力。

在微动疲劳情况下,假定微观塑性为线性累积,则损伤演化方程为:

式中:A=1/(KmCβ(2E)β)。

损伤变量为载荷循环数的函数,当N=Ni→D= 1时,Ni为微动疲劳宏观裂纹成核寿命,表示为:

式中:σeq-max和σeq-min为一个循环内的最大Von Mises等效应力和最小Von Mises等效应力,Rv为三维函数平均值,σeq-max和σeq-min以及Rv的值都可以根据有限元模型计算得到;m为Ramberg-Osgood方程中的幂常数,通常m=2;A和β为损伤参数,可通过用方程(6)对根据试验计算得到的成核寿命的拟合得到。

2 扩展寿命计算

用断裂力学方法进行微动疲劳扩展寿命预测是应用较多的一种方法。首先确定裂纹萌生的位置,然后计算裂纹尖端应力强度因子的范围ΔK。根据断裂力学方法,裂纹从假定初始裂纹长度ai扩展到临界裂纹长度af的寿命为:

式中:f(ΔK)为给定的裂纹扩展准则;C,m是材料常数。文中选用Paris裂纹扩展准则来计算扩展寿命,假定裂纹以模型Ⅰ模式扩展。在计算扩展寿命时,必须计算得到相应的应力强度因子(SIF)值。由于循环载荷裂纹的闭合作用(Kmin=0),则相应的SIF范围等于Kmax。

3 应力强度因子计算

扩展有限元可以通过数值计算来体现不连续状态,而不需要重新划分网格。这个方法由 Moës, Belystschko等[13]提出,是基于单位分解法,该方法能在标准有限元结构中导入局部节点集。研究表明,该方法能准确地计算应力强度因子[14]。

利用扩展有限元法,应力强度因子SIF计算如下:

对于平面应力:E＇=E,对于平面应变:E＇=E/(1-υ2)。

4 全寿命计算

4.1 计算方法

基于损伤力学和断裂力学的全寿命预测为:用损伤模型来计算损伤演化至宏观裂纹成核,根据从有限元模型中计算的应力应变,基于断裂力学估算微动疲劳裂纹扩展寿命;然后根据试验结果反推裂纹成核寿命,结合成核寿命方程,根据得到的成核寿命拟合得到损伤参数A和β;再利用成核寿命方程进行成核寿命计算,成核寿命和扩展寿命相加即为预测的全寿命。在计算裂纹扩展寿命时,假定初始裂纹长度ai=100 μm,根据最大等效塑性应变位置确定裂纹成核位置,裂纹方向与接触面垂直。2A12铝合金的弹性模量E=69.6 GPa,泊松比为υ= 0.33,极限强度σu=447.86 MPa,屈服强度σy= 342.02 MPa[15],扩展直到试件断裂af=3.5 mm。文献[16]研究表明,初始裂纹的选取对裂纹演化预测有一定的影响,但对最终寿命没有影响。国外通常用涡电流无损检测来检测搭接件间的微裂纹,最小可检尺寸为760 μm×380 μm的半椭圆裂纹[17],而且没有特定的准则来定义微动疲劳初始裂纹长度,介于上述原因,将初始裂纹长度选为100 μm,裂纹扩展增量Δa为10 μm。

选用2A12铝合金材料进行微动疲劳试验,微动垫半径r分别为115,180,225 mm。具体实验设备和实验方法见文献[18],试验结果和根据断裂力学计算出的扩展寿命见表1。

表1 2A12铝合金微动疲劳试验和计算结果Table 1 Test and calculation data of fretting fatigue for 2A12

估算微动疲劳全寿命的具体步骤为:

1)用ABAQUS有限元软件模拟微动疲劳接触;

2)用El Haddad参数确定过程区尺寸lc;

3)根据有限元模型从过程区中得到σeq-max,σeq-min,σ*和Rv的平均值;

4)用 XFEM模拟裂纹扩展得到扩展寿命(Np-calculated);

5) 反推裂纹成核寿命Ni-experimental=Nf-experimental-Np-calculated;

6)选取其中4个试件,根据计算的裂纹成核寿命用方程(6)来拟合得到损伤参数A和β;

7)根据拟合得到的损伤参数值和从(3)中得到的各参数,利用方程(6)可求出其余8个试件的成核寿命(Ni-estimated);

8)相加计算成核寿命和扩展寿命,得到预测的微动疲劳全寿命为Nf-predicted=Ni-estimated+Np-calculated。

4.2 参数确定

对于圆柱/平面接触微动疲劳,在接触载荷和轴向载荷作用下,接触边缘产生微观尺度的局部塑性变形,从而产生较高的应力梯度,则应力分量σeq-max,σeq-min和Rv受网格划分尺度的影响很大。为了减少网格划分尺度的影响,应用基于过程区(面)法(如图1所示),以初始裂纹成核点为过程区中心,以临界距离lc为过程区半径r,计算半圆过程区内应力分量σeq-max,σeq-min和Rv的平均值。 临界距离lc根据El Haddad参数[19]来确定,其定义为:

式中:ΔKth为长裂纹门槛应力强度因子;Δσe为光滑试件疲劳极限。对于2A12铝合金,ΔKth=2.47 MPa(m)1/2,Δσe=137 MPa,则lc=100 μm。

通过对试件有限元模型进行计算,从有限元中得到的σeq-max,σeq-min和Rv的平均值见表2。

图1 微动疲劳初始裂纹过程区Fig.1 The process zone at the location of fretting fatigue initial crack

表2 应力分量值Table 2 The data of stress components

因为损伤参数A和β为未知材料常数,从12个试验件中选取4个试验件来确定材料的损伤参数。试件包含4种不同的轴向应力状态,法向接触载荷为450 N,微动垫半径为180 mm。根据表3所选试验件过程区内σeq-max,σeq-min和Rv的平均值,将这些值代入到寿命计算方程(6)中,即可用回归分析计算试验成核寿命Ni-experimental与估算成核寿命Ni-estimated间的最小二乘拟合,从而确定损伤参数的值。试验值与估算值的误差为回归差(误差=Ni-experimental-Ni-estimated),误差总量用均方根差来估计,其公式为:

式中:n为分散数据量。非线性回归使RMSE取最小值,得到的损伤参数值见表3。损伤参数A和β与等效多轴损伤应力σ*之间的关系曲线分别如图2和图3所示,由此计算出剩余试件的损伤参数值。

图2 损伤参数β与σ*的关系Fig.2 The relationship of damage parameter β vs σ*

图3 损伤参数ln A与σ*的关系Fig.3 The relationship of damage parameter ln A vs σ*

表3 损伤参数值Table 3 Summary of damage parameters

4.3 计算结果

预测全寿命与试验全寿命的结果比较如图4所示,可以看出,预测值与实验结果比较接近,预测误差分散带都在2倍因子以内,表明基于损伤力学和断裂力学法能较好地预测微动疲劳全寿命。

图4 微动疲劳试验寿命与预测寿命比较Fig.4 Estimated fretting fatigue versus experimental lifetime

12个试验件的成核寿命所占百分比如图5所示,可以看出,对于所有试验件,随着轴向应力的增加,成核寿命减小。从总体来说,成核寿命占全寿命的较小部分,平均成核寿命占全寿命的百分比约为39%。这主要是由于在较高的应力作用下,裂纹成核非常早,扩展寿命从试件的近表面开始,因此占试件全寿命的主要部分。

图5 成核寿命百分比Fig.5 Percentage of fretting fatigue initiation lifetime

5 结论

1)微动垫和疲劳试件接触界面应力状态的多轴特性对预测微动疲劳成核寿命起到非常重要的作用,损伤力学法能考虑接触面应力三维度的作用来反映多轴状态作用,能有效模拟微动疲劳的多轴行为。

2)基于损伤力学模型和从有限元模型中提取的多轴应力状态参数,用最小二乘法确定损伤演化过程中损伤参数的值来计算成核寿命,结合扩展寿命得到全寿命。结果表明,损伤力学结合断裂力学法能有效地预测微动疲劳全寿命。

3)由于微动作用,裂纹成核非常早,与传统的疲劳试验相比,试件成核寿命较短,占全寿命的较小部分。扩展寿命从试件的近表面开始,占全寿命的主要部分。

[1] 杨茂胜.航空铝合金材料微动疲劳裂纹扩展寿命研究[J].装备环境工程,2012,9(5):5—7. YANG Mao-sheng.Study on Propagation Life of Fretting Fatigue Crack of Aerial Aluminum Alloy[J].Equipment Environmental Engineering,2012,9(5):5—7.

[2] 周文.临界面法预测微动裂纹萌生特性和微动疲劳寿命[J].润滑与密封,2010,35(6):108—111 ZHOU Wen.Predicting Fretting Fatigue Crack Initiation Behavior and Fretting Fatigue Lifetimes Using Critical Plane Approach[J].Lubrication Engineering,2010,35 (6):108—111.

[3] 杨万均.燕尾榫结构微动疲劳寿命预测方法研究[D].南京:南京航空航天大学,2007. YANG Wan-jun.Prediction Method on Fretting Fatigue Life of Dovetail Joint[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2007.

[4] 崔海涛.基于非线性连续介质损伤力学方法的微动疲劳寿命预测[J].航空学报,2013. CUI Hai-tao.Prediction of Fretting Fatigue Life Based on Nonlinear Continuum Damage Mechanics[J].Acta Aeronautica et Astronautica Sinica,2013.

[5] FAANES S.Inclined Cracks in Fretting Fatigue[J].Engng Fract Mech,1995,52:71—82.

[6] WATERHOUSE B,LINDLEY T C.Fretting Fatigue[M]. London:MEP,1994.

[7] GOLDEN P J,GRANDT A F.Fracture Mechanics Based Fretting Fatigue Life Predictions in Ti-6Al-4V[J].Engng Fract Mech,2004,71:29—43.

[8] HILLS D A,NOWELl D.Mechanics of Fretting Fatigue [M].Dordrecht:Kluwer,1994.

[9] SZOLWINSKI M P,FARRIS T N.Observation,Analysis and Prediction of Fretting Fatigue in 2024-T351 Aluminum Alloy[J].Wear,1998,221:24—36.

[10]HOUGHTON D,WAVISH P M,WILLIAMS E J,et al. Multiaxial Fretting Fatigue Testing and Prediction for Splined Couplings[J].International Journal of Fatigue, 2009,31:1805—1815.

[11]KACHANOV L M.Time of the Rupture Process under Creep Conditions[J].Izv Akad Nauk SSSR Otd Tekh Nauk,1958,8:26—31.

[12]LEMAITRE J.Engineering Damage Mechanics[M].The Netherlands:Springer,2005.

[13]MOËS N,DOLBOW J,BELYTSCHKO T.A Finite Element Method for Crack Growth without Remeshing[J]. International Journal for Numerical Methods in Engineering,1999,46:131—50.

[14]GINER E,NAVARRO C,SABSABI M.Fretting Fatigue Life Prediction Using the Extended Finite Element Method[J].International Journal of Mechanical Sciences, 2011,5:217—225.

[15]姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2004. YAO Wei-xing.Structure Fatigue Life Analysis[M].Beijing:National Defence Industry Press,2004.

[16]NAVARRO C,MUÑOZ S,DOMÍNGUEZ J.Influence of the Initiation Length in Predictions of Life in Fretting Fatigue[J].Strain,2011,47:283—291.

[17]LYKINS C D,MALL S,JAIN V K.Combined Experiment Alnumerical Investigation of Fretting Fatigue Crack Initiation[J].Int J Fatigue,2001,23(8):703—711.

[18]杨茂胜.微动对LY12CZ铝合金疲劳性能的影响[D].青岛:海军航空工程学院,2010. YANG Mao-sheng.The Effect of Fretting on LY12CZ Aluminum Alloy Fatigue Property[D].Qingdao:Naval Aeronautical Engineering University,2010.

[19]HADDAD E L,DOWLING M H,TOPPER N E,et al Integral Applications for Short Fatigue Cracks at Notches[J]. Int J Fract,1980,16(1):15—36.

Research of Fretting Fatigue Holistic Life Prediction Method for 2A12 Aluminum Alloy

CHEN Yue-liang1,XU Li1,2,ZHANG Yong1,LIU Xu1

(1.Qingdao Branch of Naval Aeronautical Engineering University,Qingdao 266041,China; 2.Institute of Naval Aviation,Huludao 125001,China)

ObjectiveThe holistic life prediction approach for fretting fatigue was proposed for 2A12 aluminum alloy based on initiation life and propagation life.MethodsThe initiation life was calculated using continuum damage mechanics approach,and the propagation life was calculated using fracture mechanics approach with SIF obtained from XFEM.The prediction life was compared with the test life.ResultsThe results indicated that the damage mechanics approach could consider the effect of the stress triaxiality which reflected the multiaxial stress state property.The model could effectivelypredict the fretting fatigue holistic life.The crack initiated quickly because of fretting,and the crack propagation began from the near surface,and the propagation life accounted for the main part of holistic life.ConclusionThe holistic life prediction model considering initiation life and propagation life was perfect,and the prediction life coincided well with the test life.

2A12 aluminum alloy;damage mechanics approach;fretting fatigue;holistic life

10.7643/issn.1672-9242.2014.04.001

TG146.2+1

:A

1672-9242(2014)04-0001-06

2014-05-14;

2014-06-07

Received:2014-05-14;Revised:2014-06-07

国家自然科学基金资助项目(51075394,51375490)

Fund:Supported by the National Natural Science Foundation of China(51075394,51375490)

陈跃良(1962—),男,浙江人,博士生导师,教授,主要研究方向为复杂环境下飞机结构寿命评定、结构疲劳与可靠性。

Biography:CHEN Yue-liang(1962—),Male,from Zhejiang,Doctoral tutor,Professor,Research focus:lifetime evaluation,fatigue and reliability of aircraft structures in complex environment.