行人友好型路口交通信号控制优化研究

张 勤，刘凌恺，邱世崇，邹 巍

（1.重庆交通大学 交通运输学院，重庆400074；2.重庆国际投资咨询集团有限公司，重庆400023）

我国是人口大国，行人交通占有很大比重，行人作为交通系统中的弱势群体其安全极易受到行驶车辆的威胁，行人的安全出行是一个非常重要的问题。为了规范交通秩序，提高行人过街效率，保障行人过街安全，交通工程师设计了多种行人过街设施，即立体过街设施从空间上将人车分离，平面过街信号控制从时间上将人车分离。在考虑行人过街因素时，在信号交叉口的控制中添加行人过街信号，为行人过街提供了可能。

研究者在考虑机动车、自行车和行人组合下的混合交通中，提出混合交通下的控制。但在交叉口的行人控制中，主要是从车辆的角度出发，对行人的考虑率只限于行人的延误，没有考虑行人的其他因素。因此，本文在控制中加入了人行横道的通行能力控制因素，加重考虑行人出行的安全性和时效性，创建行人友好型交叉口。

1 多元目标的选取

式中:si为第i相位时车行道上的机动车饱和流率；λi为第i相位的绿信比。

1.1 车行道的通行能力

1.2 人行横道的通行能力

式中:Qp为人行横道的通行能力；Gp为行人绿灯时长，s；A为人行横道的长度，m；lp为行人损失时间，一般取2s；a为行人的前后间距，取1m；B为人行横道的宽度，m；b为行人的左右间距，取0.75m；vp为行人平均步速，通常取1.2m／s；r1，r2为行人的对向干扰和到达后所产生的不均衡折减系数，分别取0.9和0.7。

1.3 机动车的延误

在实际中常用到韦伯斯特近似延误公式。韦伯斯特近似延误如下式

式中:D为车辆的平均延误；C为交叉口信号周期时长，s；G为有效绿灯时间，s；Q为车辆的到达率，pcu／h；X为饱和度；S为饱和流量，pcu／h。

1.4 行人的延误

行人延误一般分为三类:第一，行人在红灯时间，到达交叉口等待行人绿灯所形成的延误；第二，绿灯末期到达交叉口，但是不能完全通过交叉口且被车流阻断，等待可穿越间隙或者下一个绿灯所形成的延误；第三，在绿灯时间内被同相位放行的车辆阻断所形成的延误。

在一次过街情况下，信号控制下行人延误常用的计算方法如下

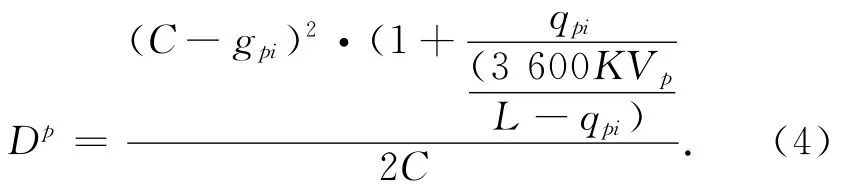
式中:C为信号的周期时长，s；qpi为行人的到达率，pcu／h；K为人行横道的宽度，取5m；L为人行横道的长度，m；Vp为行人体的速度，取1.2m／s；gpi为行人绿灯时长，s。

1.5 停车率

停车率是指车辆在交叉口受到阻碍后停车时的情况，停车率由两部分组成，正常受阻部分车辆的停车率和过饱和状况下的停车率。交叉口车辆的停车率为

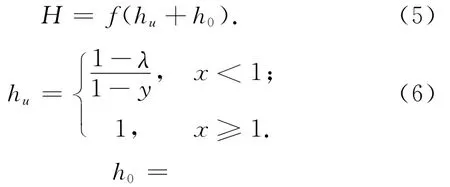
式中:f为部分车辆不完全停车的停车率矫正系数，一般取0.9；hu为正常受阻部分车辆停车率，h0为随机情况下与过饱和情况下的停车率；x0＝0.67＋；Q为进口方向车行道的通行能力，pcu／h；T为观测时长，h；S为饱和流量，pcu／h；g为有效绿灯时间，s；λ为绿信比；y为流量比；x为饱和度。

2 目标函数及求解

2.1 各个目标的权重系数

机动车和行人组成的混合交通控制，以交叉口的通行能力、人行横道的通行能力、行人的延误、机动车的延误以及车辆的停车率为信号控制性能指标，建立多元目标函数

交通需求和各种交通出行方式的流量比与信号控制具有关联性，所以，可根据流量比来确定信号控制性能指标的重要程度。流量比越大，其性能控制指标就越重要，流量比小则其重要程度也较小。

假设交叉口是由两相位控制，且每个相位的交通流有两个方向。根据流量比的情况，控制指标各自权重计算方法如下:

1）机动车延误权重为

2）行人延误权重

3）车行道的通行能力权重

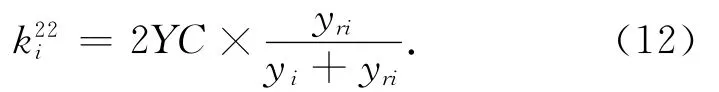
5）停车率权重

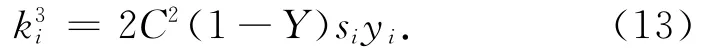
2.2 目标函数的优化及求解

交叉口的车辆和行人延误，人行横道和车行道的通行能力，车辆的停车率之和的最小值，即目标函数的最小值，也是交叉口控制优化的目标。即

求解多元目标模型具有一定的难度，一般情况下只能得到有效解，所以，采用遗传算法对目标函数进行求解。在运用遗传算法求解非线性规划时，约束条件的处理是求解的关键，目前，主要的处理技术有拒绝方法、修补方法和罚函数法，这里采用罚函数的方法来处理约束条件。罚函数的形式为

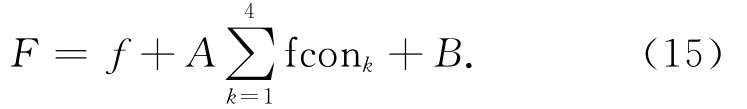
其中A＝10 000 000，为惩罚系 数；B＝0.000 000 1，B是为了防止被整除。根据式（15）中的约束条件，将fconk定义为

3 案例分析

选取重庆市某信号控制交叉口（十字型）进行案例分析，该交叉口各进口道包含左、直、右3个转向。交叉口采用四相位，即:相位一，东西直行；相位二，东西左转和右转；相位三，南北直行；相位四，南北左转和右转。交叉口的西面商业活动较多，行人流量较其他进口多，东西方向为主干道，道路较宽且车流量较多，而南北方向为次干道，道路较窄且车辆较少，通过现场调查，得到交叉口各个进口的车流量和各个方向的行人流量，如表1所示。

在遗传算法求解过程中，采用实数向量编码。其中周期和绿灯时间取值为

由于采用四相位控制，所以n＝4。经过选取不同的参数进行试算，确定算法的种群规模N＝100，交叉概率pc＝0.95，变异概率pm＝0.05，算法终止条件为迭代次数达到200次。

表1 交叉口流量

运用实际的调查数据，结合提出的多元目标模型，优化该交叉口的配时信号控制，将其结果和原始方案、Webster方法进行对比分析，结果如表2所示。

比较分析三种方法可得出无论是 Webster算法还是文中采用的算法，都与交叉口现在的方法相比周期得到优化，通行能力提高，降低延误。这里的算法与 Webster算法相比较，通行能力提高了14.1%，人行横道通行能力的提高了4.7%，行人的平均延误降低了26%，交叉口的人均延误降低了3.8%。从比较结果可以看出，该算法在不影响交叉口通行能力的情况下，提高了人行横道的通行能力，且很大程度地降低了行人过街的延误，交叉口的人均延误也有所降低。

表2 性能指标比较

4 结束语

从行人的角度出发改善交叉口的信号配时方法，在交叉口控制的目标函数中加入了行人的延误，还考虑了在行人较为集中地区的人行横道通行能力。更多地考虑了行人过街的安全性、高效性。

［1］许智.混合交通条件下信号交叉口配时优化方法研究［D］.北京:北京交通大学，2008.

［2］陈小红.混合交通环境下城市道路交通信号控制优化模型研究［D］.北京:北京交通大学，2012.

［3］冯树明，裴玉龙.行人过街延误研究［J］.哈尔滨工业大学学报，2007，39（4）:613－616.

［4］孙迪.行人过街交通行为建模［D］.吉林:吉林大学，2012.

［5］梁昔明，朱灿，颜东煌.基于物种选择的遗传算法求解约束非线性规划问题［J］.中南大学学报:自然科学版，2009，40（1）:185－189.

［6］刘权富，陆百川，马庆禄，等.平面交叉口信号控制多目标优化研究［J］.交通科技与经济，2014，16（1）:47－50.

［7］韦凌云，柴跃廷，赵玫.不等式约束的非线性规划混合遗传算法［J］.计算机工程与应用，2006，42（22）:46－49.

［8］李瑞敏，陆化普.基于遗传算法的交通信号控制多目标优化［J］.长安大学学报:自然科学版，2009，29（3）:85－88.

［9］曹成涛，徐建闽.单交叉口交通多目标控制方法［J］.计算机工程与应用，2010，46（16）:20－22.

［10］郝晨羽，刘小勇.信号交叉口通行能力计算方法适用性研究［J］.交通科技与经济，2014，16（4）:22－25.

［11］马莹莹，杨晓光.信号控制交叉口周期时长多目标优化模型及求解［J］.同济大学学报:自然科学版，2009，37（6）:761－765.