基于2R1T并联机构的自动调平控制系统设计与仿真
江涛,朱大昌
(江西理工大学机电学院,江西赣州 341000)
基于2R1T并联机构的自动调平控制系统设计与仿真
江涛,朱大昌
(江西理工大学机电学院,江西赣州 341000)
分析了基于2R1T并联机构的自动调平系统运动学特性,给出该系统仿真模型下的控制策略和条件,为了提高轨迹追踪精度和减少系统受到的不确定的参数的影响,针对该平台模型设计了一种模糊自适应控制器,控制器使用平台位置传感器反馈信号,并可在模糊化界面实时修改PID参数。仿真结果证明该控制算法比传统PID能更有效减少位置误差。
自动调平;并联机构;模糊自适应;控制策略
以往自动调平系统常采用手动调平,存在调平耗时长,自动化程度低、精度低等缺点[1-4]。研究发现两转动一平移 (2R1T)空间三自由度并联机构既具有转动和移动的运动输出特性,又具有少自由度并联机构的优点,恰好满足动基座自动调平系统调平特性,因此采用基于2R1T并联机构作为自动调平支撑机构,首先分析了此自动调平机构的调平特性,并在Matlab/Sumlink环境下,进行了模糊自适应PID控制器的设计与仿真。
1 2R1T自动调平机构的运动学特性
自动调平支撑机构的上平台是一个固定的基础,下平台为一活动平台,上下平台设计成正三角形;同时由3个分支机构将上下平台的各个顶点相连,每个分支的是由3个不同的运动副关节和两节连杆连接而成:从上到下依次为转动副、移动副、球副,如图1所示。分析可知由于连接下平台的关节只有1个自由度,致使其3个连杆只能在3个平面上活动,分別为:

不难看出限制运动平台只有两个方位上的自由度及一个轴向的线性自由度,即位置姿态的6个元素中只有3个为独立,其运动的工作空间即为自动调平机构的调平空间。

图1 自动调平系统的支撑结构空间示意图
此外平台的位置和姿态的连续变化过程影响调平机构调平性能,为了提高轨迹追踪精度和减少系统受到的不确定的参数的影响,也为了设计有效的自动调平控制器,就有必要进一步分析平台运动学特性。这里由图1可知,固定坐标系 {B}下机构的闭环约束方程为:

这里选φ,θ,ZP3个参数作为独立的输出位姿参数,且φ=-ψ,由上式可得上平台中心点两个约束方程:

2 自动调平控制器设计
PID控制器由于构造简单、性能强大而被广泛使用,但是,由于自动调平机构的多环机械结构决定其动力学模型是一组非常复杂的非线性时变方程,而且自动调平平台所基于的2R1T并联机构也存在一些不确定的参数,这些原因将限制住PID控制器可控制的范围[5]。模糊控制作为一种新型的控制方式已成功地用于各种工业过程控制中。其优点在于:不需要建立精确的数学模型,适当运用模糊规则和隶属函数,就可以在各种工业控制领域实现智能化模糊自动控制;同时具有较强的鲁棒性,被控对象参数的变化对模糊控制的影响不明显,可用于非线性、时变、时滞系统的控制。结合二者优点,调平机构选择PID参数模糊自适应控制方式实现。
所谓PID参数模糊自适应就是找出PID(Kp、Ki、Kd)3个参数与之间的模糊关系,在运行中通过不断检测,根据模糊控制原理来对3个参数进行在线修改,以满足不同时对控制参数的不同要求,而使被控对象有良好的动、静态性能。自适应控制器为了得到机构顺滑控制所设计的位置闭环控制中包含了一个模糊控制器与PID控制器基于位置反馈信息,位置误差e及误差变化率ec作为模糊控制器的输入,输出用于调整PID参数,图2所示为模糊自适应模型。
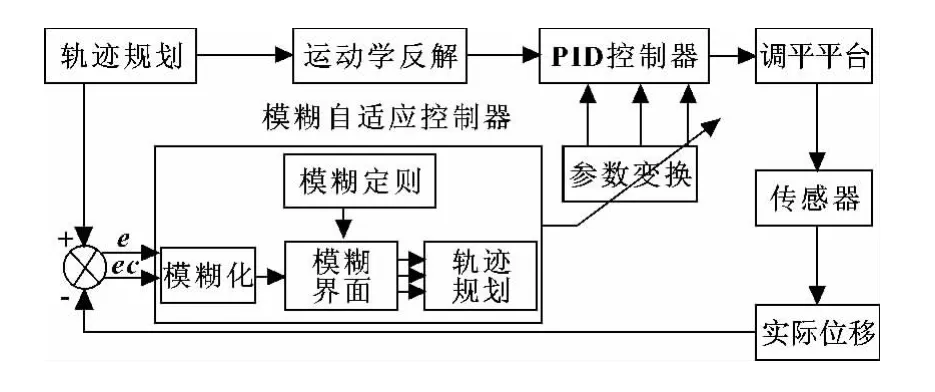
图2 模糊自适应模型
根据误差及误差变化率模糊子集的隶属度赋值表和各参数模糊控制模型,应用模糊合成推理设计分数阶PID参数的模糊矩阵表,算出参数代入下式计算:

式中:Kp0、Ki0、Kd0为PID参数的初始设计值,由传统的PID控制器的参数整定方法设计,ΔKp=(E,EC)p、ΔKi=(E,EC)i、ΔKd=(E,EC)d即为模糊控制器的3个输出,上述模糊推理过程可利用Matlab的FIS图形窗口中完成,如图3所示。

图3 模糊推理过程
在Matlab菜单窗口中输入命令Fuzzy可进入FIS编辑器,在FIS编辑器中可以设置输入、输出变量的模糊隶属度函数和模糊控制规则。根据模糊控制规则表,在Matlab的FIS编辑器中建立起模糊推理系统,然后在Sumlink中建立系统的仿真图。
3 自动调平控制系统建模
根据以上方程式推导思路,使用Matlab/Simulink仿真软件,构建系统总方块图如图4[6-7]。

图4 自动调平系统方块图
自动调平系统方块图中自动调平机构模型分为四部分:轨迹规划、运动学反解、模糊自适应PID控制器和调平平台。首先建立模糊自适应PID控制器,使用工具箱中的Simulink Response Optimization。在图4反馈回路上添加Signal Constraint模块,利用闭环回路反馈信号与目标位置之间的差,取绝对值平方根作为限制范围内所要限制的信号条件,根据此条件取符合范围内最佳收敛后的结果,作为PID控制器参数。在Simulink菜单中,选择 Fuzzy Logic Toolbox中的Fuzzy logic controller模块,并键入名字。在模块前后加上量化因子,显然前量化因子将e和ec量化为模糊量,经模糊控制规则动态处理,成为模糊控制量,再经后量化因子将其精确化,便可得到PID控制器的控制参量Kp、Ki、Kd,这样符合要求的模糊控制器便建立起来了,如图5。将模糊控制器和PID控制器分别打包后连在一起便构成了期望的复合控制器,再封装便可得上图5所示的自适应模糊PID控制器。

图5 模糊控制器方块图
图6为所构建的自动调平平台机构及其支链模型。

图6 平台机构及其支链模型图
根据方程2所示,运用 Matlab中SimMechanics模块建立起运动学反解模拟方程式,如图7所示。

图7 运动学反解方块图
现若要求上平台中心点再完成三叶玫瑰线的轨迹:

则根据三叶玫瑰线的参数方程 (7)和方程(2),在其运动学反解模块内部封装轨迹规划模块,如图8所示。
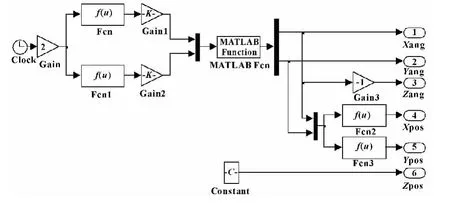
图8 轨迹规划模块
最后将上述模块搭建与自动调平机构控制仿真模型组合构成自动调平系统总方块图 (图4)。
4 仿真
首先,设定初始参数:上平台的质量为1 kg,移动副固定杆和移动杆都为0.1 kg,上平台中心点P的坐标为 (0,0,150),φ1=φ2=φ3=120°,建立机构模型(图6)。

表1 自动调平系统的支撑结构的基本尺寸
接着利用运动学反解(公式(2)—(6)与表1所示的约束条件,编程获得自动调平支撑机构的工作空间(见图9—12)。

图10 Z与θ空间

图9 平台位置空间

图11 Z与ψ空间

图12 θ与ψ空间
由上图可知自动调平支撑机构的作业空间图可知:运动平台沿x、y轴的位移范围较小,在-2.5~2.5 mm之间;绕z轴的转角φ范围较小,在-2.5°~2.5°之间;绕x、y轴的转角范围-25°~25°。同时,在机构运行过程中,绕x、y轴的转角不能同时达到极限值,平台最好工作在-10°~10°的范围内。
另外根据预设轨迹,通过反向运动学获得期望的行程和速度,从而驱动每一个支链致动器运行指定距离使得动平台完成规划轨迹,假设平台输入参考值:
EulerXYZ(-0.5sin(12πft)°,0°,0°),点P坐标输入为:(0,0,0.01sin(6πft)),在Sumlink中进行仿真,结果如图13—16所示。

图13 动平台Z轴位置变化图
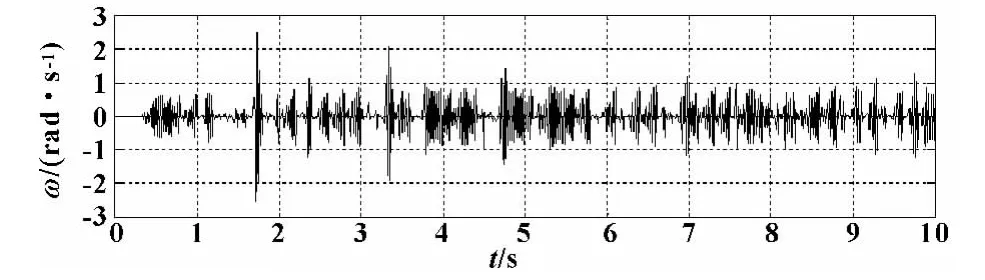
图14 动平台角速度变化图

图15 驱动杆实际输出力变化图

图16 驱动杆实际输出与参考值的差值变化偏差
改变点P参考坐标输入,设计平台中心点完成三叶玫瑰线的轨迹。图17和图18分别为规划轨迹与实际轨迹示图。

图17 规划轨迹
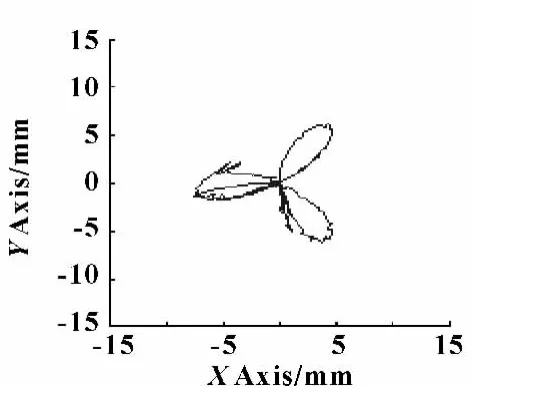
图18 实际轨迹
从图17、18可知:在平台输入的条件一定时,通过模糊自适应PID控制器的控制,动平台中心点P的X,Y,Z轴的实际位置变化与规划轨迹的变化规律一致,体现了所设计的控制器的具有较好的跟踪预定轨迹功能和制调平作用。
为了对比PID控制器与模糊自适应控制器的精度,在上述给定条件下,分别使用PID控制器与模糊自适应控制器对调平机构进行仿真模拟,图19和图20分别为其位移误差时间历程。

图19 模糊自适应控制器位移误差时间历程

图20 PID控制器位移误差时间历程
在控制方面,对比图19、20发现模糊自适应控制器比PID控制器有较短的上升时间与稳定时间和较小的误差及较好的动态追踪效果。
5 结论
利用模糊自适应PID控制器在Matlab环境中完成了两转动一平移 (2R1T)自动调平系统的运动控制,在给定条件下分析了调平机构的调平工作空间。综合以上研究认为:该自动调平系统的调平空间取决于上下平台的尺寸大小、连杆的伸缩量,以及上下平台节点的关系;同时了解到此自动调平系统为一复杂的非线性系统模型,模型的特点决定了其控制器设计的复杂性,仅使用PID控制器还不能满足需求,与传统PID控制器相比,模糊自适应PID参数控制较常规PID控制具有较小的超调量和较短的调节时间,且具有较好的动态响应特性和稳态特性,在实践中具有重要的应用价值。
[1]SHENG Ying,QIU Yuanying.An Automatic Adjusting Algorithm For The Hydraulic Platform With Six Legs[J].Journal of Xidian University:Natural Science,2003,29 (5):594-597.
[2]ZHU Dachan.Study of Automatic Leveling System for Vehicle-borne Radar Antenna Based on Parallel Support Mechanism[M].Doctoral dissertation,2008.
[3]江涛,朱大昌.基于2R1T并联机构的自动调平控制系统设计与仿真[J].机电工程技术,2013,42(3):31-34.
[4]KUN DaSu.A Neural Fuzzy InferenceNetwork for Controlling of 3-DOF moving Platform[D].Master dissertation,2004,Taiwan.
[5]朱大昌,严智敏.3-RPS并联机器人位置分析及控制仿真[J].有色金属科学与工程,2012,3(1):95-100.
[6]曲中英,翁正新.基于Simulink的Stewart平台仿真研究[J].计算机仿真,2005,22(4):264-268.
[7]汪汇.3-RRRT并联机器人运动仿真的SimMechanics实现[J].现代机械,2008(3):44-48.
Design and Simulation of Automatic Leveling Control System of Parallel Support Mechanism Based on 2R1T
JIANG Tao,ZHU Dachang
(College of Mechanical and Electrical Control Engineering,Jiangxi University of Science and Technology,Ganzhou Jiangxi 341000,China)
The motion characteristics about automatic leveling system of parallel mechanisms based on 2R1T were analyzed,the control strategies and conditions for the simulation model were given.In order to improve the accuracy of position tracking and weaken the influence of uncertain parameters on automatic leveling system,a practical fuzzy adaptive controller was designed based on the kinematics of parallel platform,where fuzzy inference units were utilized to modify the PID parameters in real-time by using the position feedback from the robot actuators.The virtual experiment results demonstrate that the proposed algorithm is able to effectively reduce the position tracking errors compared with the traditional PID controller.
Automatic leveling;Parallel manipulator;Fuzzy adaptive algorithm;Control strategy
TH242.2
A
1001-3881(2014)9-013-4
10.3969/j.issn.1001-3881.2014.09.004
2013-05-13
国家自然科学基金资助项目 (50965007)
江涛 (1972—),男,讲师,研究方向为机器人技术与有限元分析。E-mail:jwtxh@163.com。

