交叉杆Stewart并联机构静刚度分析和设计

赵若愚，方喜峰，张胜文，汪通悦，刘远伟

(江苏科技大学机械工程学院，江苏镇江 212003)

交叉杆Stewart并联机构静刚度分析和设计

赵若愚，方喜峰，张胜文，汪通悦，刘远伟

(江苏科技大学机械工程学院，江苏镇江 212003)

并联机构应用于数控加工设备时要求具有很高的刚度，交叉杆机构将原有Stewart机构的3对驱动杆交错分布，使得其在运动过程中可以平均分配驱动杆的伸长量。为了验证该型机构的刚度性能，采用罗德里格斯参数方法构建了交叉杆并联机构的雅可比矩阵，推导出该型机构的刚度计算公式，分析了其在不同位置时的最小刚度和两个方向的单项刚度，并给出了其在工作空间中的分布规律。通过与传统Stewart构型的对比分析得出交叉杆并联机构的机构特点与设计优势，为这种机构的应用和开发提供了理论依据。

并联机构;静刚度;雅克比矩阵;罗德里格斯参数

6自由度Stewart型并联机构由于兼具承载力强与高速轻质的优点，被广泛应用于各种运动模拟设备中，近年来又被应用于数控加工设备的研制之中。为了满足数控机床高速重载的需求，以结构刚度、灵巧性及奇异性分析为基础的运动性能分析成为了机床设计中的一个研究重点［1］。交叉杆并联机构是平面平台型Stewart并联机构的改进形式，其动平台采用上下双层结构，6个顶点交叉布置，在牺牲了部分工作空间的前提下，可以在运动过程中平均分配各驱动杆的伸长量，以达到增强结构刚度的目的。国内外诸多学者对机床静刚度作了大量的研究。GOSSELIN等［2］采用弹簧单元描述了虚拟铰链的变形，建立了6自由度并联机构的刚柔耦合静刚度矩阵模型。PASHKEVICH等［3］在研究了6维弹簧虚拟铰链的建模方法并计算了几种典型过约束机构的结构刚度。AGINAGA等［4］以6-RUS并联机构为对象研究了奇异性轨迹与机床刚度的关系。PORTMAN等［5］采用共线刚度值的概念描述了含有奇异性轨迹的Gough-Stewart机构的静刚度，测定出了一定刚度要求下的机床工作空间。在国内，李育文等［6］考虑了并联机床支链与机架的变形，采用有限元法分析了6-UPS并联机床的静刚度并进行了实验验证。韩书葵等［7］采用螺旋理论推导出了4自由度并联机器人的刚度计算公式并进行了分析。王友渔、汪满新等［8－9］在少自由度并联机床的刚度研究上做了大量工作，建立了Tricept、Bicept等机器人的刚度模型。

文中采用罗德里格斯参数构造出机构的雅克比矩阵，推导出并联机构一般刚度系数和各单项刚度系数的关系式，对比分析了交叉杆并联机构及传统Stewart机构的最小刚度、最大刚度和单向刚度，显示出两种结构不同的特点与优势，对该型机构的设计具有一定的指导意义。

1 并联机构的雅克比矩阵

交叉杆型并联机床上定义两个坐标系，动坐标系即工具坐标系OA-xAyAzA固定在动平台上，坐标原点OA在动平台下层几何设计中心上;静坐标系即基础坐标系OB-xByBzB固定在定平台上，坐标原点OB在定平台几何设计中心。其实物图与结构如图1所示。

图1 交叉杆型并联机床

任意一对顶点之间的连杆矢量可以表示为

式中:lk为杆的长度;

ek为杆的方向单位矢量;

ak为动平台顶点在动坐标系中的矢量，表示ak=(ax，kay，kaz，k)T，k=1，2，…，6;

bk为定平台顶点在静坐标系中的矢量，表示为bk=(bx，kby，k0)T，k=1，2，…，6。

矢量P=(PxPyPz)T描述动平台参考点在静坐标系的位置矢量，动平台的姿态矩阵采用罗德里格斯矩阵的表示方式。Sx、Sy、Sz为3个独立的罗德里格斯参数，旋转矩阵R可以表示为R=［I－S］－1［I+S］，式中，I是3阶单位矩阵，S是由3个独立参数表示的反对称矩阵，其表达式为

将式 (2)代入旋转矩阵之中，得到由罗德里格斯参数表示的旋转矩阵，其表达式为

将式 (1)两边取时间的导数，等式左边即为驱动杆的输入速度;定义一个速度旋量Vk=［v，ω］，则各驱动杆速度与动平台位置速度的关系为

其中J即为运动雅克比矩阵，可以表示为

式中:ei为各驱动杆速度沿其运动方向的单位矢量，表示为(bi－Rai)/‖bi－Rai‖。

2 并联机构的刚度系数

2.1 一般刚度系数

假设并联机构的动、静平台皆为刚体，只考虑各运动分支的关节刚度，根据胡克定律，可以得到某一驱动杆上，微小力变量与关节变化量的关系为

将所有驱动杆上的变化量集合为一个整体，上式又可以表示为

其中:ki是由各运动分支刚度系数组成的对角矩阵，将动平台运动速度和各驱动杆运动速度的映射关系Δq=J·Δp代入式 (7)，可以得到

考虑在静力平衡时，动平台受力与各运动分支间的受力关系

将式(8)与式(9)相结合，即得到动平台受力与其运动变量之间的关系

令K=JTkiJ，K即是并联机构的刚度矩阵。

由于ki为一个对角矩阵，再根据雅克比矩阵的性质，可以知道机构的刚度矩阵是一个实Hermite矩阵，根据正规阵的性质可知，存在一个标准正交的矩阵V，使得K可以分解为

其中，Λ=diag［λ1，λ2，…，λ6］，是刚度矩阵的6个特征值，将其排列为一个升序序列，表示为

相应地，V=［v1，v2，…，v6］表示为对应于各特征值的特征向量。其物理意义可以表示为当有一个沿着v1方向的力施加在动平台上，其在空间上会产生一个沿着v1方向的运动旋量。由于τ和Δp在形式上表现为6维向量，根据KHASAWNEH［10］的方法将刚度系数表示为两个向量模长的比值

根据上述公式，即可得到并联机构在空间中的最小和最大刚度系数及其对应的运动旋量。

2.2 单向刚度系数

由一般刚度系数的推导可以看出，作用在动平台上的任意一个力旋量都会产生唯一的运动旋量与之对应。因此，将并联机构刚度矩阵的特征向量矩阵看作是空间的一组基，则力旋量作用于动平台上产生的微小运动旋量都可以表示为该组基上坐标与特征向量的线性组合，即为

再根据公式 (10)，该力旋量可以表示为

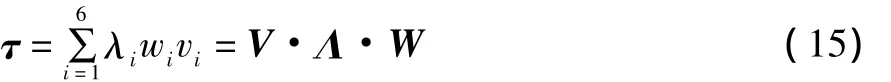
取力旋量与运动旋量的内积，得到

将式(16)和式(17)代入到式(13)中即可得到单向刚度系数S'的计算公式如下

3 机构的刚度仿真与对比分析

表1是交叉杆并联机床的基本参数，考虑驱动杆及铰链等材料均为钢，选取材料弹性模量为E=200 GPa，驱动杆的截面尺寸半径为52.5 mm，初始位置时静平台中心到动平台中心距离Zp=900 mm，计算得到两组杆长L1=1 013 mm、L2=977 mm。

表1 动、静平台顶点坐标 (交叉杆机构)

根据图1所示动、静平台分为内外两圈，静平台外圈半径Rb=643.5 mm，动平台外圈半径为Ra=405 mm。将其作为一般Stewart并联机构的动、静平台半径，可以得到该机构动、静平台的顶点坐标如表2所示。

表2 动、静平台顶点坐标 (一般Stewart机构)

图2表示交叉杆并联机构以及一般Stewart机构动平台在Z=900 mm平面上 (相对于静坐标系)的最小刚度曲线图。图4、5显示了两个机构在x、y两个单向的刚度系数。通过计算结果可以看出，两种机构的刚度分布曲线趋势较为相似，但交叉杆型机构的在最小刚度及两个单项刚度的刚度系数均高于一般Stewart机构，验证了其初始设计构想。并且交叉杆型机构在x、y两方向的刚度系数值中心对称性更好，不足之处在于其中出现了突变拐点，y方向的刚度变化波动较大。

图2 最小刚度曲线图

图3 交叉杆构型单项刚度曲线图

图4 Stewart构型单项刚度曲线图

表3 部分位姿下两种机构的刚度比较 105N/mm

表3给出了两种机构的动平台在C1(φx=0，φy=0，φz=0，x=0，y=0，z=－900)，C2(φx= 0，φy=0，φz=0，x=－155，y=－155，z=－1 100)，C3(φx=10°，φy=－10°，φz=15°，x=0，y=0，z=－900)，C4(φx=10°，φy=－10°，φz=15°，x=－155，y=－155，z=－1 100)4种位姿下的最小刚度及x、y方向单项刚度系数，计算结果表明:交叉杆机构在不同位置下的刚度更高，且x、y两方向的刚度系数值较为接近，在工作空间中受位置及姿态变化的影响较小。

4 结论

(1)通过对交叉杆型并联机构与一般Stewart机构的分析，可以看出两者静刚度系数随坐标值的变化具有相近似的变化趋势，但交叉杆构型的单项刚度系数的中心对称性更好，在不同位姿下的刚度性能好于一般Stewart机构。

(2)Stewart型并联机构的静刚度与其动静平台的铰点位置选取有着密切的关系，其构型设计及机构参数优化时需要考虑到工作空间中静刚度随位姿的变化。

［1］程世利，吴洪涛，王超群，等.平面平台型Stewart并联机构的奇异性分析［J］.机械工程学报，2011，47(9):1－7.

［2］GOSSELIN C M，ZHANG D.Stiffness Analysis of Parallel Mechanisms Using a Lumped Model［J］.International Journal of Robotics and Auto-mation，2002，17(1):17－27.

［3］PASHKEVICH A，CHABLAT D，WENGER P.Stiffness A-nalysis of Overconstrained Parallel Manipulators［J］.Mechanism and Machine Theory，2009，44(5):966－982.

［4］AGINAGA J，ZABALZA I，ALTUZARRA O，et al.Improving Static Stiffness of the 6-RUS Parallel Manipulator U-sing Inverse Singularities［J］.Robotics and Computer-Integrated Manu-facturing，2012，28:458－471.

［5］PORTMAN V T，CHAPSKY V S，SHNEOR Y.Workspace of Parallel Kinematics Machines with Minimum Stiffness Limits:Collinear Stiffness Value Based Approach［J］.Mechanism and Machine Theory，2012，49:67－86.

［6］李育文，张华，杨建新，等.6-UPS并联机床静刚度的有限元分析和实验研究［J］.中国机械工程，2004，15(2): 112－115.

［7］韩书葵，方跃法，槐创锋.4自由度并联机器人刚度分析［J］.机械工程学报，2006，42(增刊):31－34.

［8］王友渔，黄田，CHETWYND D G，等.Tricept机械手静刚度解析建模方法［J］.机械工程学报，2008，44(8):13－19.

［9］汪满新，王攀峰，宋轶民，等.4自由度混联机器人静刚度分析［J］.机械工程学报，2011，47(15):9－16.

［10］EI-KHASAWNEH B S，FERREIRA P M.Computation of stiffness and stiffness bounds for Parallel link manipulators［J］.Machine Tools＆Manufacture，1999(39):321－342.

Analysis of Stiffness and Design for Stewart Parallel Mechanism of Cross Rods

ZHAO Ruoyu，FANG Xifeng，ZHANG Shengwen，WANG Tongyue，LIU Yuanwei
(School of Mechanical Engineering of Jiangsu University of Science and Technology，Zhenjiang Jiangsu 212003，China)

The high stiffness is required when the parallel mechanism is used in the machine tool.As three pairs of active rods in the manipulator are crossed，which is different from the original Stewart mechanism，the length of each rod are average distributed.In order to verify the stiffness performance of this parallel mechanism，Lodrigues parameters were used to build the Jacobian，and the expression of stiffness was given.The minimum stiffness and single stiffness in several different direction were described，and the stiffness distributions throughout the entire task workplace were given.The characteristics and advantages are shown through the comparative analysis，and the results offer the evidence for the design as well as the use of this type of parallel mechanism.

Parallel mechanism;Stiffness;Jacobian;Lodrigues parameters

TG502

A

1001－3881(2014)9－025－4

10.3969/j.issn.1001－3881.2014.09.007

2013－05－15

国家自然基金资助项目 (50375071);江苏省重点实验室开放基金资助项目 (HGDML-0809，CJ0905);江苏省普通高校研究生创新计划资助项目 (CXLX12_0686)

赵若愚 (1987—)，硕士，研究方向为并联机构与多体动力学。E－mail:roy.sikong@163.com。