3-CRC并联机构构型变异与性能分析
陈海真,宋宏鹏
(山东理工大学,山东淄博 255049)
3-CRC并联机构构型变异与性能分析
陈海真,宋宏鹏
(山东理工大学,山东淄博 255049)
通过改变已有3-CRC并联机构运动支链的配置方式,得到了一类运动完全解耦的新型三平移并联机构,并导出了机构的位置正反解方程。利用机构的完全解耦性与位置方程导出了机构工作空间的解析表达式,并对两类机构的解耦性能与工作空间进行了对比,验证了新机构优良的运动性能,为其后续的研究和应用提供了依据。
并联机构;机构构型;位置正、反解;解耦;工作空间
运动解耦、工作空间体积大的少自由度并联机构具有优良的运动性能,实用价值较高,具有广泛的应用前景[1-2]。运动解耦性与并联机构的结构形式有着密切的关系,其位置分析相对也比较复杂,工作空间的求解受到多种因素的影响,较难得到一个精确的解析解。目前多数是利用数值方法对工作空间求近似解,少数机构可以根据其特定的结构形式和位置方程得到解析解[3]。为了更好地推广应用少自由度并联机构,通过对其拓扑结构进行分析,寻求运动解耦性优良、工作空间体积大的结构形式尤其重要。
1 机构构型的变异
图1所示为文献 [4]中提出的3-CRC并联机构。动平台的运动输出矩阵是3条CRC支链的运动输出矩阵的交集,通过改变3条运动支链的布置方式可以得到其他形式的3-CRC并联机构。将3条支链的驱动副由三角形分布改为正方形分布,可以得到图2所示的3种类型的3-CRC并联机构。

图2 第二类3-CRC并联机构简图
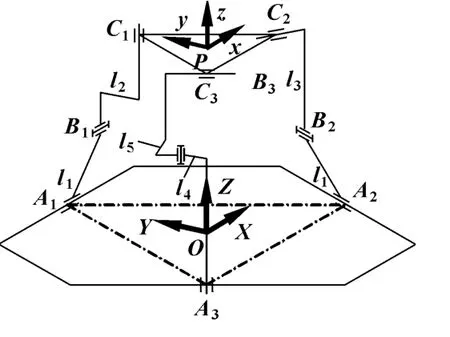
图1 第一类3-CRC并联机构简图

各条支路运动输出矩阵的交集为并联机构的运动输出矩阵[5]。
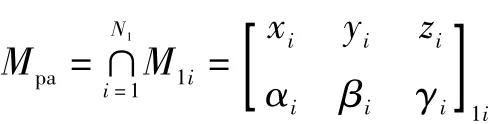
式中:Mpa为并联机构动平台的运动输出矩阵;
M1i为第i条支路的运动输出矩阵。
据上式,可得图2中的3类机构的运动输出矩阵。
对于图2(a)所示的机构,其运动输出矩阵:

对于图2(b)所示的机构,其运动输出矩阵:

对于图2(c)所示的机构,其运动输出矩阵:

由式(1)、(2)、(3)可见,新机构(a)、(b)在输出特征上满足预期要求,机构 (c)的自由度发生了变化,增加了一个绕空间y轴的转动自由度,且机构在y方向的移动失去了运动输入的约束,因此该类机构不再具备三平移的运动特征。
2 机构的位置分析
图1所示3-CRC1并联机构的位置正解、反解方程[4]分别为

对图2(a)所示3-CRC2机构,建立如图所示坐标系。支链A1B1C1的输入角θ1沿Y轴负向逆时针为正,支链A2B2C2的输入角θ2取沿Y轴正向逆时针为正,支链A3B3C3的输入角θ3则沿Z轴正向顺时针为正。杆A1B1、A2B2、A30B3的长度均为l1,B1B10、B2B20、B30C30的长度分别是l2、l3、l4。由图可知点P坐标 (xp,yp,zp)即为动平台在定坐标系O-XYZ中的位置坐标。据矢量关系

可得以下方程

由上述三式可得该机构的位置正解、反解方程分别为

对比、两式和对图2(a)的分析可以看出,图2(b)所示机构具有完全相同的解,且机构的位置解仅与三条支链的杆长有关,不受上下平台尺寸的影响,因此图2(a)、2(b)所示两机构在进行位置和工作空间分析时可归为一类 (但在动力学和静刚度性能上两机构会有差别)。
3 运动解耦性分析
下面根据并联机构输入输出组解耦的定义[6]依据位置正解方程,分析两类机构的解耦特性。将两类机构的输入、输出分别用向量θ=(θ1θ2θ3)T、X= (xpypzp)T表示。并联机构3-CRC1,由式可知输出组X中的xp与输入组θ中的θ1、θ3有关,而yp只与θ1有关,zp仅与θ2有关,所以该机构属于输入输出部分组解耦。
并联机构3-CRC2,由式可知输出组X中的不同元素都唯一地对应输入组θ中的一个元素,该机构输入输出完全解耦,比3-CRC1机构具有更好的运动学性能。将式两端分别对时间求导得机构输入与输出速度向量之间的关系式,即运动Jacobian矩阵
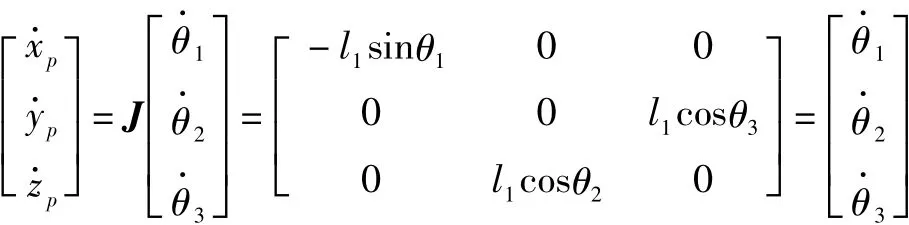

4 机构的工作空间分析
4.1 影响并联机构工作空间的因素
杆长、运动副转角的限制以及连杆的运动干涉等[7]是影响并联机构工作空间大小的主要因素。影响3-CRC并联机构工作空间的主要结构参数是C副的移动行程和转动副的转角行程。据这两类3-CRC并联机构的特点,若满足C副移动行程的约束条件,转动副的转角约束条件自然满足。下平台3个支链C副的移动距离用si(i=1、2、3)表示,上平台3个支链C副的移动距离则用di(i=1、2、3)表示,两类机构的C副移动行程约束条件表式如下:

根据机构的结构特点和几何关系可以得出3-CRC1并联机构,上下平台各支链C副的位移表达式

式中:z0为点P z方向的初始坐标,θ20、θ30分别为2、3支链驱动副的初始位置角。
对于并联机构3-CRC2,上下平台各支链C副的位移表达式

式中:x0、y0、z0为点P的初始坐标。
4.2 工作空间的求解
大部分并联机构由于其工作空间是不规则的空间几何体,无法求出其精确的解析解,只能借助软件近似模拟工作空间的形状,并用数值方法求出其体积的近似解。
据前面的分析知3-CRC2并联机构完全解耦,位置解方程简单,可以根据其位置正解方程,并综合考虑影响工作空间大小的约束条件,求出以点P为参考点的动平台工作空间的集合表达式。据式 (6)、(8)、(9)、(12)及(13)可以求出3-CRC2并联机构工作空间的集合表达式

由式 (14)可以得出工作空间的体积为(2l1)3或(cmax-cmin)3,据具体机构的结构参数取两者计算结果的小值。按表1中所给的3-CRC2并联机构的结构参数,可得工作空间的体积理论值为2.7×107mm3。
用极坐标搜索法可求两类机构工作空间的数值解。据3-CRC并联机构的位置反解方程可求解工作空间。把驱动杆的转角θ1、θ2、θ3及C副的位移si、di用动平台点P的位置坐标 (xp,yp,zp)表示出来,若机构符合各种约束条件,该位置点在工作空间内,否则在工作空间外。利用MATLAB编制边界搜索程序,可得两类机构的相关结构参数及工作空间体积值,见表1。图3为两类机构的工作空间三维立体图。

表1 机构结构参数与工作空间体积
由表1对比发现,3-CRC2并联机构工作空间体积数值计算结果为2.689 6×107mm3,与理论值的误差是0.386 5%,证明了工作空间解析解的正确性。
由图3可以看出两类机构的工作空间,3-CRC1的工作空间形状复杂,其边界存在很多尖角,尖角区域机构工作性能较差,而3-CRC2的工作空间外形是规则的立方体,而且在整体尺寸相同的情况下工作空间体积值增加了1.681倍,明显地改善了其工作性能。
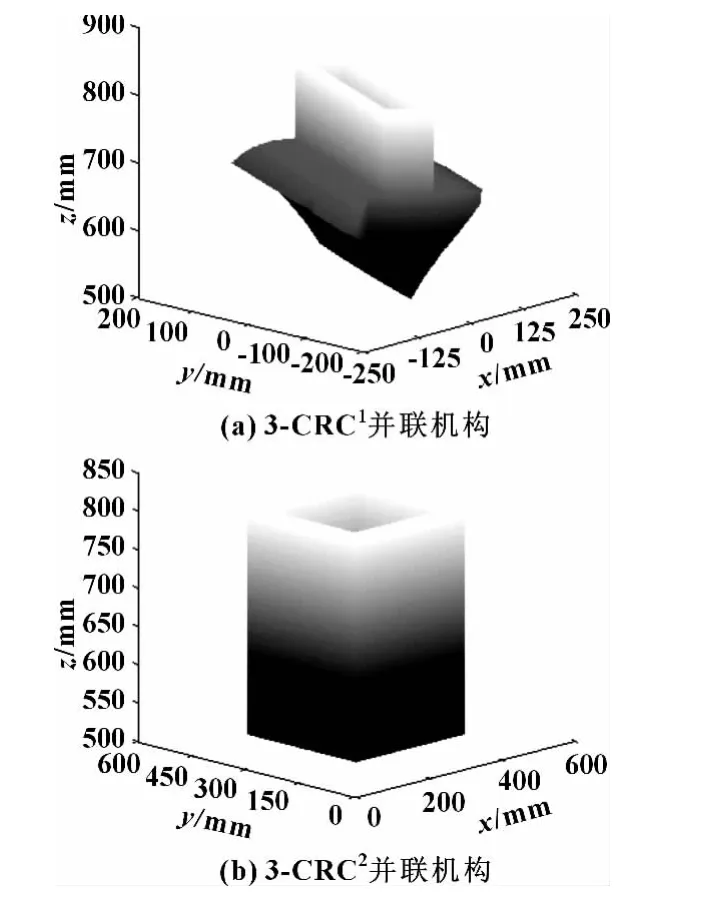
图3 工作空间三维立体图
5 结论
并联机构具有复杂多样的拓扑结构,且运动支链配置方式的不同往往会引起机构运动特性的巨大改变。通过对3-CRC机型进行构型变异和分析,得到了具有更加优良运动性能的机型,新机构位置正反解方程简单、运动完全解耦,机构的控制方案简单,且工作空间体积得到了成倍的提高。研究结果对该类机构的实际应用具有重要意义。
[1]黄真,李秦川.少自由度并联机器人机构的型综合原理[J].中国科学(E辑),2003,33(9):813-819.
[2]张彦斌,吴鑫,刘宏昭.一种新型3-CRP移动并联机构的设计和运动分析[J].中国机械工程,2008,19(4): 435-438.
[3]LI H D,GOSSELIN C M,MARC J R,et al.Analytic Form of the Six-Dimensional Singularity Locus of the General Gough-Stewart Platform[C].Proc.ASME DETC 2004/ MECH-57135,2004b,Salt Lake City,Utah,USA.
[4]邹忠月,陈海真,宋宏鹏.新型3-CRC并联机构结构及运动解耦分析[J].山东理工大学学报:自然科学版,2009,23(1):29-32.
[5]杨廷力.机器人机构拓扑结构学[M].北京:机械工业出版社,2004.
[6]宫金良,张彦斐,高峰.并联机构的解耦特性[J].中国机械工程,2006,17(14):1509-1512.
[7]MASORY O,WANG J.On the Accuracy of a Stewart Platform-Part II Kinematic Calibration and Compensation[C].Proc.IEEE Conf.on Rob.1993,Aut,725-731.
Variations in Configuration and Performance Analysis of 3-CRC Parallel Mechanism
CHEN Haizhen,SONG Hongpeng
(Shandong University of Technology,Zibo Shandong 255049,China)
A new type of parallel mechanism with three-dimensional(3D)translations and movement complete decoupling was generated by changing the configuration form of the movement branched-chains of the original 3-CRC parallel mechanism,and the positional forward and inverse solution equations were derived.The analytical expression of workspace of mechanism was derived from using the complete decoupling and positional equations of the mechanism,and the decoupling performance and workspace of two types of mechanisms were compared.The excellent kinematics performance of the new mechanisms is verified,which provides a basis for further application and study.
Parallel mechanism;Mechanism configuration;Positional forward and inverse solution;Decoupling;Workspace
TH112
A
1001-3881(2014)9-021-4
10.3969/j.issn.1001-3881.2014.09.006
2013-04-22
山东省自然科学基金资助项目 (Y2006G17)
陈海真 (1963—),女,硕士,副教授,研究方向为机构学与创新设计。E-mail:chhaizhen@163.com。

