再担保体系内银保风险共担研究
——基于系统动力学
梅 强,许红珍
(江苏大学管理学院,江苏 镇江 212013)
再担保体系内银保风险共担研究
——基于系统动力学
梅 强,许红珍
(江苏大学管理学院,江苏 镇江 212013)
近年来,我国中小企业信用再担保体系的发展为中小企业融资做出了巨大贡献,但作为贷款风险分散机构,担保机构、再担保机构在与银行合作过程中一直处于弱势地位。我国再担保机构一直致力于完善银保合作机制,加强银保沟通,实现银保风险共担。国外一些再担保体系在银保风险共担方面相对比较成熟,值得我国再担保体系学习和借鉴。本文以再担保机构、担保机构和合作银行为研究对象,运用系统动力学,建立中小企业信用再担保体系动态仿真模型。将江苏省再担保数据,代入模型仿真模拟,研究银保风险共担对信用再担保体系系统模型内主体经济收益的影响,研究结果表明,银行在银保合作中承担一定风险,可以抵御代偿率增加对再担保体系发展的负面影响,在一定程度上能够保证再担保体系的可持续发展,从而保证银行能够获得更为长远的利益。
中小企业;信用再担保;银保风险共担;企业融资
一、引言
担保行业的发展有效缓解了我国中小企业融资难问题,银保合作的贷款模式下银行需要承担的放贷风险全部转嫁至担保机构。我国大部分担保机构规模小,资本少,其在银行合作中承担高风险,实现低收益,难以健康发展,我国为了扶持担保业的发展,逐步在各省份成立再担保机构,以期其为担保机构分担风险,增加信用,从而帮助更多中小企业解决融资问题。与银行建立良好稳定的协作关系有利于信用再担保体系的长期平稳运作,国际上很多国家在银保合作方面都有先进经验值得学习和借鉴。美国、日本的协作银行在担保项目中承担20%~30%风险责任,韩国的协作银行也需承担25%~30%的风险责任,且韩国法律要求金融机构必须按其每年贷款规模的0.2%向韩国信用保证基金联合会和地方信用保证基金提供无偿捐助[1-2]。且国外的协作银行对再担保体系的授信倍数高达20倍、30倍甚至50倍[3]。
我国再担保体系经过几年发展,各自取得一定成就。我国的再担保机构在成立之初,积极努力改善银保关系,为再担保体系内担保机构寻求优惠政策,力求实现银保风险共担。然而银行为自身利益考虑,在银保合作中不愿或不会主动去承担风险。我国在风险共担方面有迈出脚步,但进程缓慢。东北再担保与个别银行达成协议,合作银行分担风险比例突破25%,广东也创建了银行、担保、再担保的三方风险分担机制,江苏再担保与部分银行签订战略合作协议,有三家合作银行同意承担10%~20%的风险分担比例。要靠银行自主意愿来实现风险共担是不太现实的,我国没有相应的法律法规,再担保想要实现银保风险共担,任重而道远。
二、再担保体系经济收益系统模型构建
1.建模的基本思想
鉴于上面提到的再担保体系内银保风险共担问题,构建仿真再担保体系经济收益系统动力学模型主要研究以下问题:①探讨银行在银保合作中承担一定风险对再担保体系内主体经济收益的影响;②探讨在银行承担风险责任时,如何保证银行经济收益增长;③探讨银保风险共担在保证再担保体系持续发展中有何积极作用。
2.因果关系分析
在明确建模目的的基础上,根据系统动力学理论的系统因素分析理念,确定影响再担保体系经济收益的主要构成因素,运用Vensim软件绘制再担保体系经济收益的系统因果关系图[4],如图1所示。
3.再担保体系经济收益的系统流图
上述对系统因果关系的分析,主要表达了系统要素之间的相关性和反馈过程。这是对系统的定性分析,但这种分析无法描述系统管理和控制过程[5]。因此,为克服这一问题,引入流位变量(Level)、流率变量(Rate)、辅助变量和常数变量等,构造更加深入的系统流程图[6]。系统流程图不仅保持了因果关系图所含的因果关系、反馈回路关系,更重要的是用流位和流率变量定量地描述再担保体系经济收益的系统,从而更具体、更全面地描述系统从结构到行为演变和系统因素相互作用的机制[7]。如图2所示,为运用Vensim软件绘制再担保体系经济收益的系统流图。
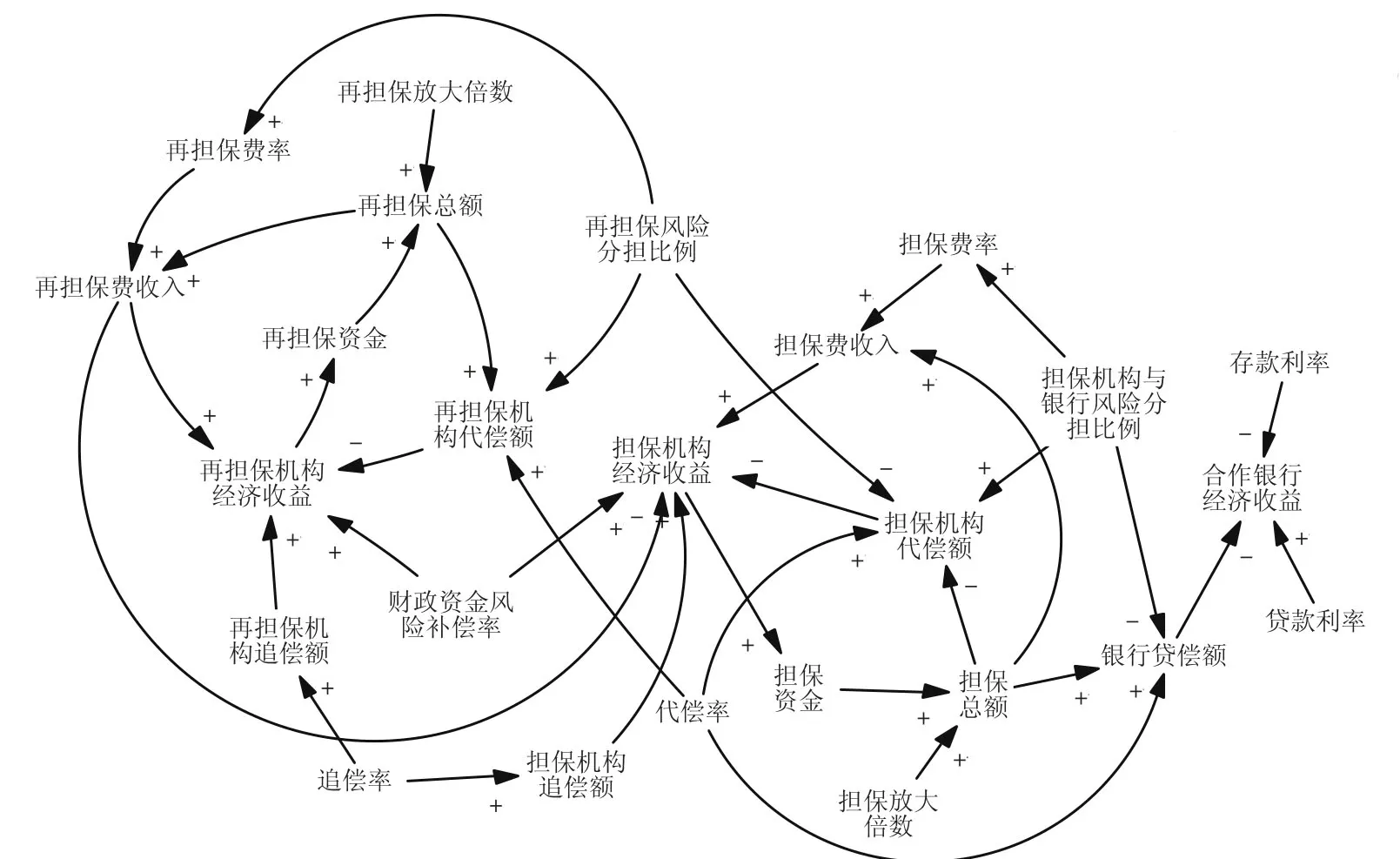
图1 再担保体系经济收益因果关系图
三、模型仿真分析
1.方程构造
方程的建立是系统动力学模型中至关重要的一个环节,通过对系统流图中各变量进行赋值、建立数学方程关系式,实现继对研究对象的定性描述后的定量分析。建立方程的目的是为了是模型能够运用计算机仿真模拟,来研究模型假设中所隐含的系统动力学特性,确定解决问题的方法和对策建议。
本模型中有三个水平(状态) 变量方程,分别为:L再担保机构经济收益=INTEG(再担保费收入-再担保机构代偿额+再担保机构追偿额+再担保风险补偿额,0);L担保机构经济收益= INTEG(担保费收入-担保机构代偿额+担保机构追偿额+担保风险补偿额-再担保费收入,0);L合作银行经济收益= INTEG(贷款利息-存款利息-银行代偿额,0)。六个速率变量方程为:R再担保费收入=再担保费率×担保费收入;R再担保机构代偿额=再担保总额×代偿率×担保机构与银行风险分担比例×再担保风险分担比例;R担保费收入=担保总额×担保费率×担保机构与银行风险分担比例;R担保机构代偿额=担保总额×代偿率×担保机构与银行风险分担比例×(1-再担保风险分担比例);R贷款利息=担保总额×贷款利率;R存款利息=担保总额×存款利率。其余为辅助变量方程及常量,方程中的常数变量及相关系数在模拟过程中会有所变化,因此,本研究全部使用字母代替。A代偿率=a1;A再担保总额=再担保资金×再担保放大倍数;A再担保放大倍数=b1;A再担保机构追偿额=再担保机构代偿额×追偿率;A再担保费率=c1×再担保风险分担比例;A再担保资金=M1;A再担保风险分担比例=d1;A担保总额=担保放大倍数×担保资金;A担保放大倍数=b2;A担保机构与银行风险分担比例=d2;A担保机构追偿额=担保机构代偿额×追偿率;A担保费率=c2×担保机构与银行风险分担比例;A担保资金=M2;A再担保风险补偿额=财政资金风险补偿率×(再担保机构代偿额-再担保机构追偿额);A担保风险补偿额=财政资金风险补偿率×(担保机构代偿额-担保机构追偿额);A财政资金风险补偿率=e;A贷款利率=r1;A存款利率=r2;A追偿率=a2; A银行代偿额=担保总额×代偿率×(1-担保机构与银行风险分担比例)。 其中 a1,a2,b1,b2,c1,c2,d1,d2,M1,M2,r1,r2,e为常数变量。
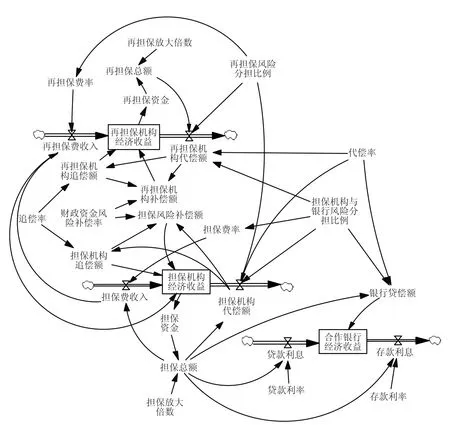
图2 再担保体系经济收益的系统流图
2.模型基本假设
在建立再担保体系经济收益仿真模型中,主要进行以下几个方面的基本假设:①再担保总额与担保总额等同,本文研究的是由再担保机构再担保的担保行为,再担保总额就等于担保总额。②再担保放大倍数等于担保放大倍数。③模拟周期为20年。
3.模型的参数估计
本模型的仿真是在Vensim PLE环境中完成的,取INITIAL TIME= 0,FINAL TIME=20,即模拟运行20年,TIME STEP=1,时间单位为年。本文以江苏省数据进行仿真模拟。江苏省2012年再担保总额为550亿元,担保平均放大倍数为6倍,担保费率为1%,再担保费率为30%,再担保承担50%风险,银行不承担风险,代偿率为1%,追偿率为60%,现商业银行的存款利率为3%(存期为一年利率),贷款利率为6.15%(贷款期为1-3年利率)。故变量取值为:a1=0.01,a2=0.6,b1=6,b2=6,c1=0.6,c2=0.01,d1=0.5,d2=1,M1=100,M2=100,r1= 0.0615,r2=0.03,e=0。
4.系统对担保机构与银行风险分担比例的灵敏度分析
在原模型中改变担保机构与银行风险分担比例,如图3所示,图中曲线1~6分别表示担保机构与银行风险分担比例及对应担保费率为(1,0.01)、(0.9,0.0095)、(0.85,0.00925)、(0.8,0.009)、(0.75,0.00875)、(0.7,0.0085)时,系统各主体经济收益变化。
从图3可以看出,当担保机构与银行风险分担比例减小时,担保、再担保机构的经济收益都有所增加,合作银行的经济收益有所减少。担保机构与银行风险分担比例越小,即银行需要承担的风险越大,当出现代偿时,银行需要承担的代偿额越大,在贷款利息减存款利息不变的情况下,银行经济收益减少是必然的。这也是银行不愿意承担风险的原因。在这个模型里,设置的担保费率并不是不变的,它随着担保机构与银行风险分担比例的减小而减小,随之担保费收入、再担保费收入都减少。而担保机构与银行风险分担比例减少,则担保代偿额、再担保代偿额也都减少,这在反面增加了担保机构、再担保机构的收益。
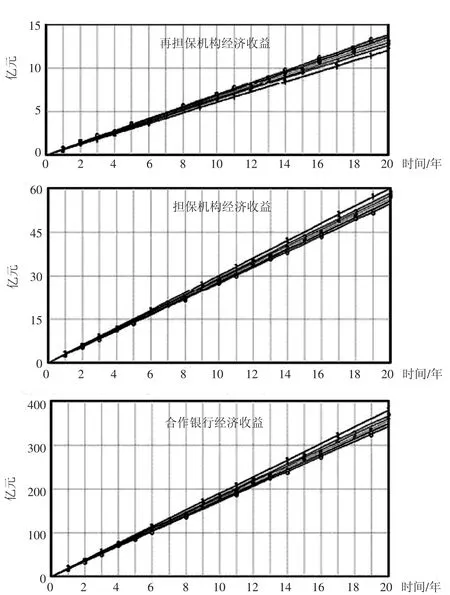
图3 系统对担保机构与银行风险分担比例的灵敏度分析

表1 模型对比分析

图4 合作银行经济收益分析
5.合作银行经济收益分析
上述分析表明,合作银行经济收益受担保机构与银行风险分担比例影响,当银行承担风险时,银行经济收益会减少,这也是银行不愿意承担风险的原因,但这是在放大倍数不变的情况下。如何在增加银行承担风险比例时,不减少银行的经济收益,放大倍数是关键。下面同时改变担保机构与银行风险分担比例和放大倍数进行仿真模拟。如表1设置担保机构与银行风险分担比例和放大倍数,其中b1(b2)为放大倍数,d2为担保机构与银行的风险分担比例,c2为担保费率。运行得到结果如图4所示,图中曲线1~6分别对应表中1~6列参数取值。
从图4可以看出,当银行承担风险比例增加时,担保倍数只要小幅度上升,银行的经济收益都会得到增加,当放大倍数增加到20时,即使银行承担30%的风险,银行的经济收益还是显著上升。以上结果可以为银行考虑是否承担风险、承担多少风险提供参考,为我国实现银保风险共担提供依据。
6.银保风险共担作用研究
从再担保体系本身的发展来看,增加放大倍数可以促进再担保体系更好的发展。从社会效益角度来看,增加放大倍数可以直接增加再担保总额,扩大再担保体系服务规模,解决更多中小微企业的融资问题。政府成立再担保机构,建设再担保体系的初衷就是为了扶持中小微企业的发展,解决中小微企业的融资问题。所以不管从再担保体系发展角度考虑,还是政府期望,增加放大倍数势在必行。然而在现实情况中,随着担保放大倍数的增加,中小微企业融资规模扩大,代偿率必然随之增加。在现实里,再担保体系为了减少代偿损失,控制代偿率,严格控制风险,相对应的,部分有潜力的中小微企业被拒之门外,与扶持中小微企业发展的目标相违背。下面进行系统模拟仿真,对比在再担保倍数增加,代偿率随之增加时,借鉴国外再担保体系的经验,设置合理的担保机构与银行的风险分担比例时再担保体系内各主体经济的收益变化。如表2所示为设置的变量参数值。其中b1(b2)为放大倍数,d2为担保机构与银行的风险分担比例,c2为担保费率,a1为代偿率。
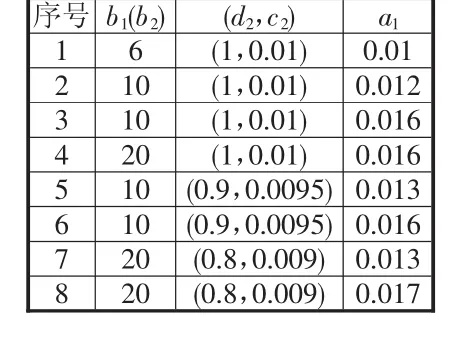
表2 参数设置取值
表2中序号1为参考现实数据的参数取值,与图5中曲线1结果对应,为原模型结果。序号2~8为交叉改变放大倍数、担保机构与银行的风险分担比例及代偿率。按表2设置变量,得到以下运行结果如图5所示,表2中序号1~8的变量取值对应图5中曲线1~8表示结果。
从图5中可知,当代偿率增加时,最先受到冲击的是再担保机构的经济收益,在再担保机构的生存都受到威胁时,对应的担保机构、合作银行的经济收益还高于原模型中担保机构、合作银行的经济收益。所以保证再担保机构有一定经济收益就能保证再担保体系的可持续发展。图5再担保经济收益图中,对比曲线1、2可以看出,当放大倍数由6倍增加到10倍时,可以容忍代偿率由0.01增加到0.012,此时,再担保机构的经济收益可以相对持平。曲线3表示,当代偿率增加到0.016时,再担保机构会有所亏损,此时增加放大倍数到20倍,检验是否能改变再担保机构的亏损结果,得到曲线4的结果表明,当代偿率增加到一定值时,增加放大倍数并不能改变再担保机构的亏损趋势,甚至相比之前亏损更严重。增加放大倍数并不能提高再担保机构对代偿率的容忍范围,此时尝试增加合作银行的风险分担比例,检验结果会有何改变。对比图中曲线3、4、6可以看出,当代偿率增加到0.016时,增加银行风险分担比例,能减缓再担保机构收益的减少。对比曲线1、5可以看出,放大倍数增加,代偿率随之由0.01增加到0.013时,银行承担一定比例风险,再担保机构经济收益只有小幅度减少,有效增强了再担保机构对代偿率的抵御能力。对比曲线5、7可以看出,放大倍数增加可以显著提高再担保机构的经济收益。曲线6、8的结果表明,放大倍数为10,银行承担10%的风险,代偿率可以容忍在0.016以下,放大倍数增加至20,银行承担20%的风险,代偿率可以容忍在0.017以下,而担保机构与合作银行的经济收益大幅度提高,放大倍数增加对应再担保总额也成倍增加,所取得的社会效益也更明显。从图5中担保机构经济收益及合作银行经济收益图可以看出,放大倍数增加,这两者经济收益明显提高。放大倍数保持在10倍或20倍时,代偿率增加会减少担保机构的经济收益,但模型设置的增加范围明显影响不到其持续发展,甚至远高于原模型中担保机构的经济收益。合作银行的经济收益比原模型增加更多,代偿率对其影响微乎其微。
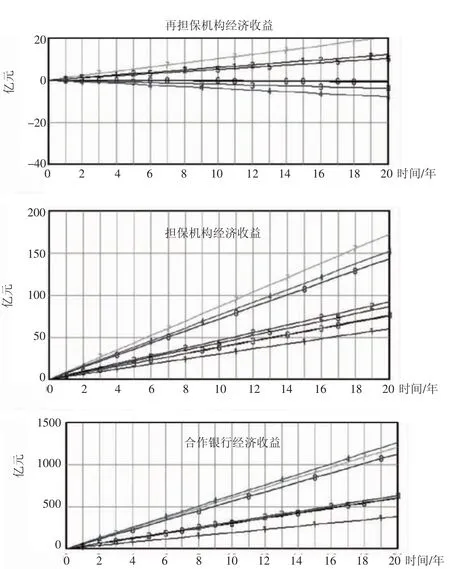
图5 再担保体系各主体经济收益变化图
四、结论
我国在银保风险共担方面处于探索阶段,本文仿真模拟结果说明银行增加风险分担比例对防御代偿率增加等方面的积极作用。在银保合作中,处于主导地位的银行,担不担风险及分担多少风险都由其意愿决定。从银行角度来看,再担保体系的建立,一方面为银行贷款降低了风险,银行更为放心放贷,扩大了贷款规模,增加了经济收益;另一方面银行与再担保体系内担保机构合作,减少了审查过程,降低了贷款成本。从眼前利益来看,银行承担风险责任,意味着会有风险损失,减少了银行的经济收益,但从长远利益来看,银行承担一定风险,可以促进再担保体系的持续发展,实现更为长远的利益。从本文仿真模拟结果可以看出,银行就算承担一定比例风险,当放大倍数同时增加时,银行的经济收益并不会减少,反而会有所增加。另外,银行分担一定风险,可以抵御代偿率增加对再担保体系发展的负面影响,在一定程度上能够保证再担保体系的可持续发展。只有再担保体系持续发展下去,银行才能获得更为长远的利益。不管从完善再担保体系方面还是银行自身利益来看,建立银保风险共担机制势在必行。
[1]叶斌.中日韩三国再担保制度比较分析 [J].华北金融,2007 (11):57-59.
[2]文学舟,梅强.日美意三种模式信用担保机构的国际比较与借鉴 [J].经济问题探索,2011(7):174-179.
[3]孙昌兴,张春梅.中国中小企业信用再担保制度的构建 [J].河海大学学报:哲学社会科学版,2011,13(1):62-66.
[4]张波.系统动力学简介及其相关软件综述 [J].环境与可持续发展,2010(2):1-3.
[5]王其藩.高级系统动力学 [M].北京:清华大学出版社,1995.
[6]Katsuhiko O.System Dynamics[M].New Jersey:Prentice Hall,2003.
[7]William J P.System Dynamics[M].Montreal:McGraw-Hill Higher Education,2005.
(责任编辑:FMX)
The Study of Bank-guarantee Risk Sharing in Re-guarantee System——Based on System Dynamics
MEI Qiang,XU Hong-zhen
(School of Management,Jiangsu University,Zhenjiang Jiangsu 212013,China)
In recent years,the development of credit re-guarantee system for Medium-Sized Enterprises(SME)has made great contribution for SME finance in China.As loan risk diversification institution,guarantee and re-guarantee institutions are always at weak positions when they are cooperating with banks.The re-guarantee institutions in China are trying to commit to improve the cooperation mechanism of bank-guarantee,strengthening communication and achieving bank-guarantee risk sharing. The re-guarantee system of risk sharing in some foreign countries is relatively mature and worthy to learn.The re-guarantee institutions,guarantee institutions and cooperative banks have been studied,and the dynamic simulated model of credit re-guarantee system for SME has been constructed.Re-guarantee data from Jiangsu Province have been calculated in the simulated model.The important influences of bank-guarantee risk sharing to the benefits from credit re-guarantee system model have been researched. The results show that banks assuming a certain risk in the process of cooperating with the guarantee institutions can resist the negative effects in development of re-guarantee system with the increasing of compensatory rate.The certain extent of cooperation ensures the sustainable development of re-guarantee system in order to ensure banks to get more long-term interests.
Small and medium-sized enterprises;Creditre-guarantee;Bank and insurance risk-sharing;Corporate financing
F727
A
1004-292X(2014)02-0078-05
2013-05-02
梅 强(1961-),男,江苏镇江人,副校长,院长,教授,博士生导师,主要从事中小企业信用再担保研究。

