单细胞分析仪中步进电机的定位控制

金 路，罗晓曙，姜东东

（广西师范大学 电子工程学院，桂林 541004）

当前，单细胞分析仪是跨学科研究的前沿和热点，在单细胞分析仪中，要实现细胞的观测和成像，必须对细胞的进样平台进行精确定位，同时对激光光源进行选择，采用步进电机进行精确定位的设计，精度高，不受各种干扰因素的影响，在定位过程中无累积误差，易于控制，性能可靠[1]。

步进电机作为一种特种电机，与直流和交流电机不同，其接收的是脉冲信号的控制，能直接将脉冲信号转化成角位移，因此适用于数字化时代[2]。步进电机的定位控制方式分为开环控制和闭环控制。传统的开环控制，由于电机的步距角固定，且不存在位置反馈，难以达到高精度的定位要求。现在的仪器设备中，步进电机一般采用PID闭环控制，对定位精度有一定的改善，但PID控制器多依靠经验或实验方法设计，效果难以令人满意[3]。

针对单细胞分析仪对单个细胞观测时要求定位精度高的特点，同时结合步进电机运行时的非线性及低频振荡等特性，运用神经网络在控制过程中自学习和自适应不确定系统的特点，将神经网络与PID结合，采用RBF神经网络与PID结合的方法实现步进电机的高精度定位，同时考虑到RBF神经网络参数初始值的选择对控制性能有很大影响[4]，因此，引入遗传算法实现对RBF神经网络初始值的优化。

1 两相混合式步进电机数学模型

对于单细胞分析仪器中的两相混合式步进电机，要得到建立其仿真的数学模型，需要进行一些简化，忽略绕组自感的二次谐波分量以及两相绕组间的互感对电机绕组电压的影响，假设两相绕组的电阻值相等。

两相混合步进电机绕组的电压平衡方程为

两相混合式步进电机的转矩方程为

电机转速和角速度的关系为

式（1）～式（4）构成了两相混合式步进电机的数学模型。其微分方程为

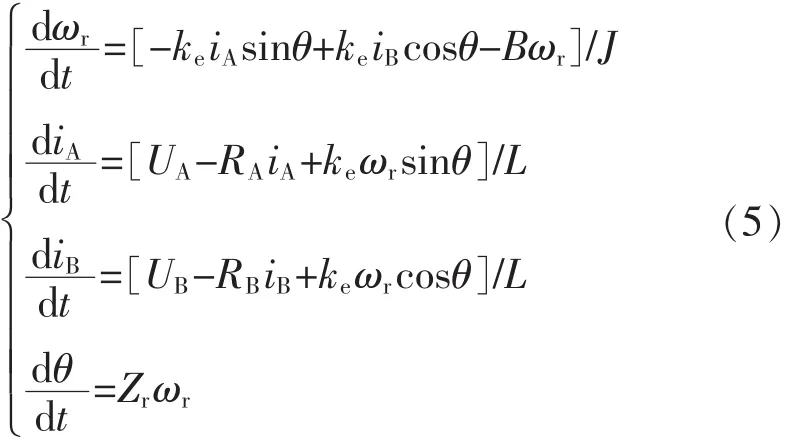
2 RBF神经网络PID控制器

2.1 PID算法

传统PID的控制方法为

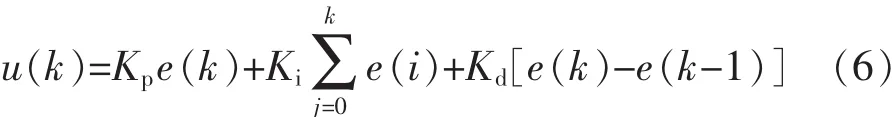
式（6）是位置式PID，在实际运行时，如果控制器受到干扰，则该方法易造成控制对象的位置突变。增量式PID克服了这一缺点。其算法为

Kp、Ki、Kd3个参数用来调整PID控制器性能的好坏。

2.2 RBF神经网络算法

RBF神经网络是一种3层前向型结构。包含输入层、隐含层和输出层，具有全局最优、运算量小、速度快、以及最佳逼近性能等优点，训练方法快速易行的特点[10]。

其网络输出为

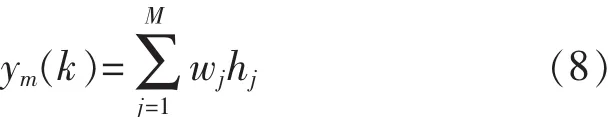
在RBF神经网络中，设其输入向量为X=［x1，x2，…，xn］T；权矢量为 W=［w1，w2，…，wm］T；径向基矢量为 H=［h1，h2，…，hm］T；径向基函数为 hj（·），取为高斯函数：

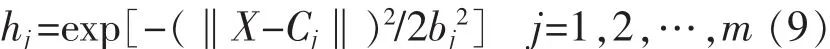
RBF神经网络的性能指标为

由RBF神经网络可以辨识得到反映被控对象的输出对控制输入变化灵敏度的Jacobian矩阵，其算法为

2.3 RBF神经网络PID控制器设计

将RBF神经网络与PID结合，利用神经网络的自适应能力，整定PID控制器的Kp、Ki、Kd3个参数。

PID控制器的输入由不同时刻反馈的位置与给定的位置误差计算得到：

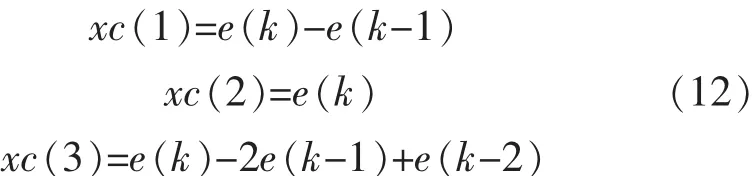
PID控制器的参数采用梯度下降法得到：

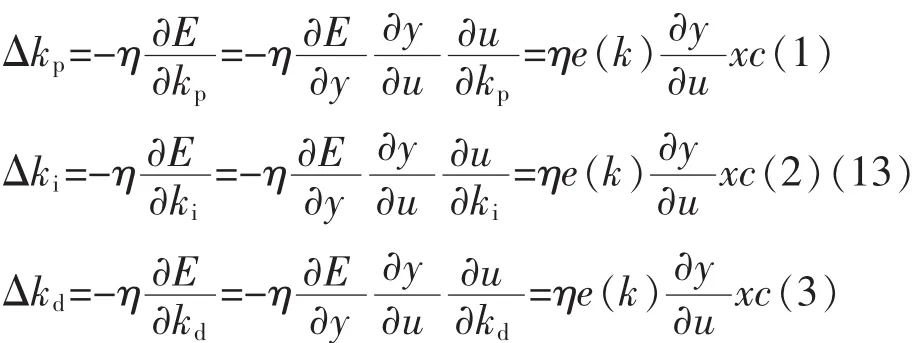
3 遗传算法优化RBF神经网络的设计

3.1 遗传算法

在RBF神经网络算法中，神经网络的连接权值、基函数的中心和宽度，这些值的选取对于RBF神经网络的性能有很大的影响[4]，本文选用遗传算法对神经网络的参数初始值进行优化，以达到最佳控制性能。

遗传算法模拟自然选择和遗传过程中繁殖、交换、变异的现象，根据优胜劣汰的自然法则利用遗传算子进行选择、交叉、变异逐代产生、优选个体，并设置适应度函数对个体优劣进行评价，直至获得最优解[5]。基于遗传算法优化的RBF神经网络与PID相结合的闭环控制器结构如图1所示。

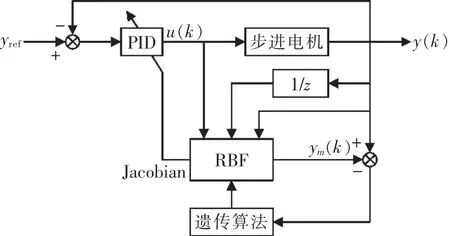
图1 遗传算法优化RBF神经网络PID控制器结构图Fig.1 RBF-PID controller with GA optimization

3.2 遗传算法优化RBF神经网络实现

遗传算法优化RBF神经网络流程图如图2所示。

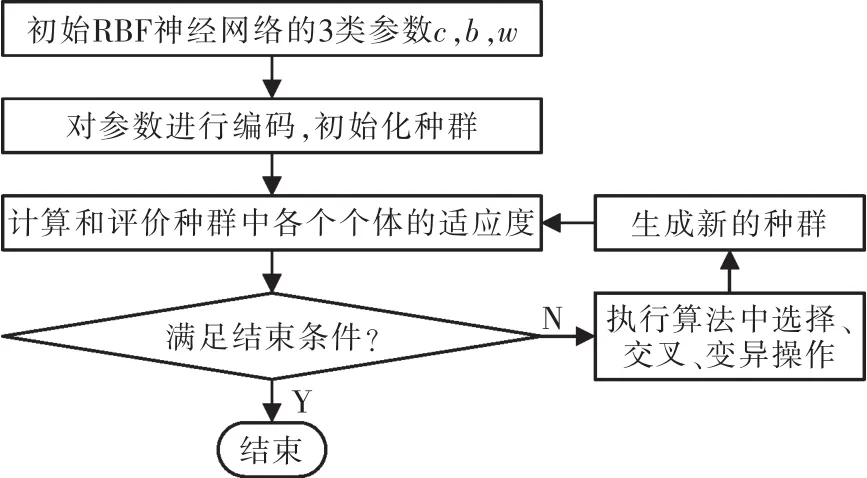
图2 遗传算法流程图Fig.2 Genetic algorithms flow chart

具体步骤：

1）编码：随机产生初始种群，采用浮点数编码，每个个体对应RBF网络的中心、宽度、权重、方式为不同的中心和对应的宽度顺次排列完成后再排列权重，即：c11，…，c1n，…，cm1，…，cmn；b1，…，bm；w1，…，wm。设定中心、宽度、权重的取值范围。

2）适应度函数的确定：适应度函数用于评价个体的效益。本文中重点在于步进电机的定位控制。控制器的优劣可由控制器的实际输出y与给定输出yref的误差大小来衡量，因此选取 F（xi）为

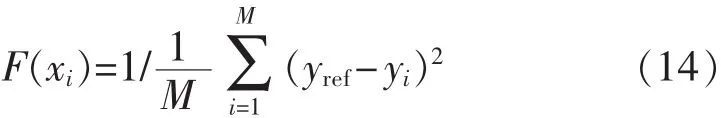
式中，M为训练的样本数。

3）选择：采用赌轮盘选择，个体被选中的概率与其适应度函数值的大小成正比。种群规模为N，个体适应度为F（xi），则个体被选中遗传到下一代的概率为

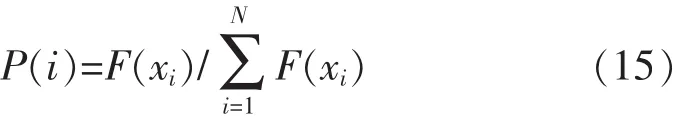
交叉：随机选中2个个体，按照一定的规则进行某些位置上的字符交换，产生新的个体。

变异：模拟了生物中的基因突变，本文采用的变异方法是按位变异。

终止条件：当适应度函数的值大于一个常数或者进化到最大遗传代数时，则结束。结束时最大的适应度函数值所对应的个体的编码串即为所求的解。

4 仿真模型搭建

本文采用Matlab/Simulink平台进行仿真，利用其中的神经网络工具箱和遗传算法工具箱。根据前文的步进电机数学模型搭建步进电机仿真子模块。RBF神经网络算法和遗传算法使用仿真软件中相应的工具箱，编写成S函数的形式，系统整体仿真模型，如图3所示。

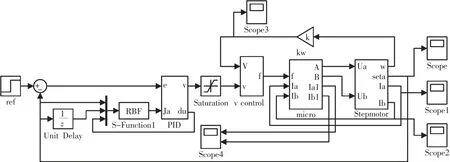
图3 系统仿真模型图Fig.3 Model diagram of system simulation

图中，系统输入的给定位置为5rad，stepmotor子模块为自建的步进电机模块，输出分别为转速w、角位移seta、两相绕组的电流值Ia、Ib。仿真中，遗传算法S函数和RBF神经网络S函数之间的参数传递，通过定义全局变量的形式实现。PID模块接收RBF辨识后输出的Jacobian矩阵的值，对相应的参数进行整定。micro模块为细分模块，由于步进电机在制造工艺上难以实现较小的步距角，加之细胞尺寸小、仪器中的物镜视角有限，因此，要实现适合于单细胞分析仪器中对定位精度的要求，必须对步进电机进行细分控制，通过控制两相绕组中的电流，实现步距角的细分，同时也能减小电机运行时的低频振荡[6-9]。图4为步进电机在开环时，直接驱动的效果。图5是在电流采用64细分时，角位移的输出波形，可以看到细分后，步进电机角位移波形更加平稳，低频振荡明显降低。

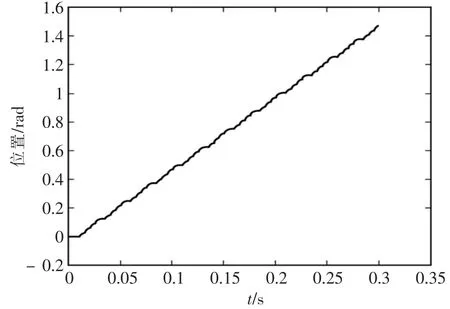
图4 未细分角位移Fig.4 Angular displacement with no subdivision

图5 细分后角位移Fig.5 Angular displacement with subdivision

5 仿真试验分析

步进电机的仿真参数选取如表1所示。

表1 仿真参数Tab.1 Simulation parameters

RBF神经网络取3-6-1结构，网络的输入为X=［Δu，y（k），y（k-1）］T，神经网络的学习速率取为η=0.32，动量因子 α=0.05；比例、积分、微分的学习速率分别为 ηp=0.45、ηi=0.25、ηd=0.4；PID 控制器中的参数为 Kp=50、Ki=0.1、Kd=1。

在优化神经网络的遗传算法中，设个体数目为50，代沟为0.9，交叉概率Px=0.8，变异概率 Pm=0.4，最大遗传代数为 50 代。需要优化的参数 cij、bj、wj，其中 i=1，2，3； j=1，2，…，6。 则性能指标 J的优化过程如图6所示。

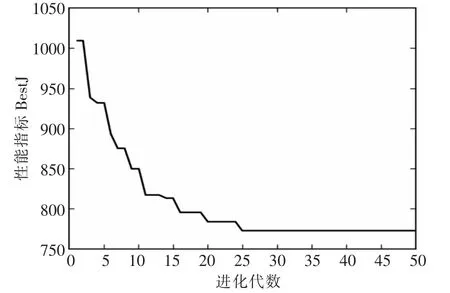
图6 性能指标优化输出Fig.6 Optimal output of performance index

整个系统控制器以及不同控制器对定位控制的仿真结果如图7所示。

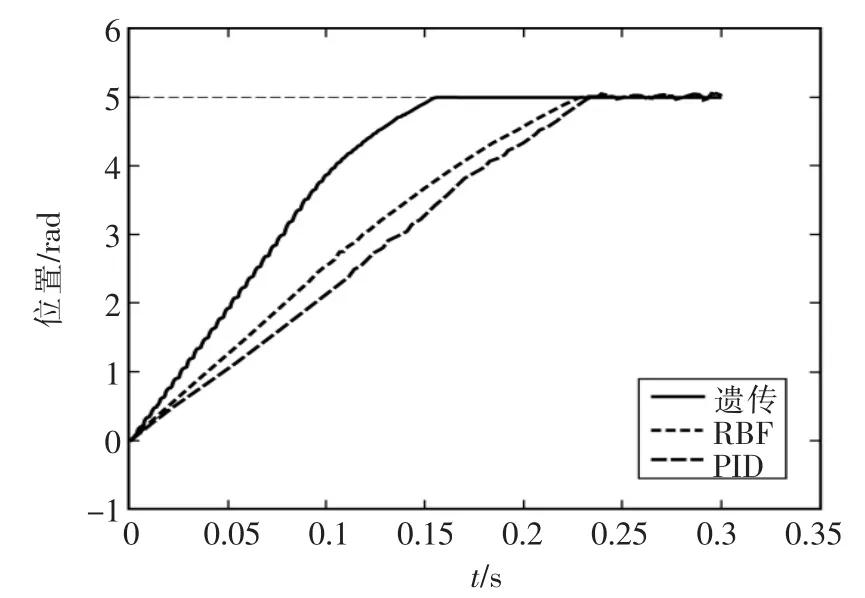
图7 三种控制器位移仿真Fig.7 Displacement simulation of three controller

突加扰动时，2种控制器对定位控制的仿真结果如图8所示。

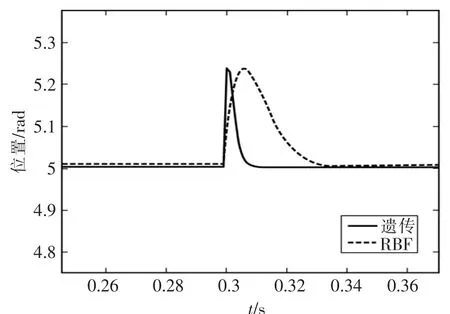
图8 突加扰动时位移仿真Fig.8 Displacement simulation with disturbance

从图7几种控制器的仿真结果对比可以看出，在定位控制过程中，传统PID控制器和RBF神经网络整定参数的PID控制器在定位时响应速度慢（在0.2 s之后），且传统PID控制在给定位置处出现超调和抖动的情况，定位精度不高。采用遗传算法优化的RBF神经网络PID控制器，响应时间短（0.15 s），无超调，定位更为快速，定位位置更精确，在步进电机的定位控制上相比前两者取得了较好的效果。在图8中，步进电机到达设定位置后，在0.3 s时突加一个扰动，可以看出，遗传算法优化后的控制器相比RBF神经网络PID控制器消除扰动更快速，定位更精确，效果较好。仿真结果基本可以满足单细胞检测仪器对定位精度的要求。

6 结语

本文针对单细胞分析仪器中，对应用步进电机进行定位控制的基础上，分析步进电机运行过程中的非线性特点，建立步进电机的数学模型并构建其仿真模块，将遗传算法与RBF神经网络和PID控制相结合，设计基于遗传算法优化的RBF神经网络PID控制器，并采用不同的控制器对步进电机定位效果进行仿真对比，仿真结果表明，本文设计的控制器，定位响应时间短，在平衡位置无超调，效果优于对比的其他控制器。

[1] 张新荣，徐保国.基于正弦细分驱动技术的步进电机控制系统设计[J].电测与仪表，2010，47（8）：69-72.

[2] 丛自龙，袁朝辉，杨芳.基于模糊自适应PID控制的定位系统设计[J].机床与液压，2013，41（7）：138-142.

[3] 周黎，杨世洪，高晓东.步进电机控制系统建模及运行曲线仿真[J].电机与控制学报，2011，15（1）：20-25.

[4] 王爽心，杨辉，张秀霞.基于混沌遗传算法的主汽温系统RBFPID 控制[J].中国电机工程学报，2008，28（23）：87-92.

[5] 单文桃，陈小安，合烨，等.基于免疫遗传算法的模糊径向基函数神经网络在高速电主轴中的应用[J].机械工程学报，2013，49（23）：167-173.

[6] Bindu V，Unnikrishnan A，Gopikakumari R.Adaptive fuzzy logic position control of a stepper motor with extended kalman filter[C]//Power，Signals，Controls and Computation（EPSCICON），2012 International Conference on.IEEE，2012：1-6.

[7] Baluta G.Microstepping mode for stepper motor control[C]//Signals，Circuits and Systems，2007.ISSCS 2007.International Symposium on，2007.

[8] Chen T C，Su Y C.High performance algorithm realization on FPGA for stepper motor controller[C]//SICE Annual Conference，2008.IEEE，2008：1390-1395.

[9] Ahmadi A，Sedehi M T，Yazdani A M，et al.Designing an optimal Fuzzy-PID controller for speed tracking of stepper motor[C]//Industrial Electronics and Applications（ISIEA），2012 IEEE Symposium on.IEEE，2012：193-198.

[10]Li Z，Hu J，Huo X.PID control based on RBF neural network for ship steering[C]//Information and Communication Technologies（WICT），2012 World Congress on.IEEE，2012：1076-1080.■