基于鲁棒Kalman滤波的猎扫雷作战过程建模及效果评估

任东彦，孙明太，周利辉

(海军航空工程学院青岛校区，山东青岛 266041）

基于鲁棒Kalman滤波的猎扫雷作战过程建模及效果评估

任东彦，孙明太，周利辉

(海军航空工程学院青岛校区，山东青岛 266041）

针对混布雷阵在猎扫雷作战效果评估中评估精度差的问题，采用时变带未建模动态系统对猎扫雷作战过程建模，通过引入带未知时变均值和方差阵的虚拟白噪声来补偿猎扫雷作战数学模型建立过程中简化带来的未知模型误差，并采用鲁棒Kalman滤波器对作战效果进行评估。仿真结果表明，该方法可有效改善Kalman滤波器的性能，对混布雷阵有很好的评估效果，评估过程和评估效果更贴近实际。

作战效果评估;鲁棒Kalman滤波器;虚拟噪声补偿技术

0 引言

猎扫雷作战效果评估是衡量反水雷作战成功与否的根本标准。研究猎扫雷作战效果评估问题时，首先必须建立猎扫雷作战过程数学模型。在这项工作中，必须全面考虑评估需求、已知条件和评估手段，深入了解作战过程的本质和具体过程，在合理简化的基础上实现数学抽象，得到作战过程最基本的规律;其次必须针对模型及相应的观测数据，提出可靠的评估方法［1］。将复杂的猎扫雷作战过程与现代最先进的理论算法联系起来，可以充分利用这些理论成果，从而使猎扫雷作战效果评估方法上升到理论高度。

猎扫雷作战效果评估问题，归根到底是误差处理问题。猎扫雷作战过程中涉及的数据很多，而每个数据都多少存在误差，其中既有系统性的，又有随机性的。如果所有数据的误差情况都分别考虑，最终将导致评估模型过于复杂，其稳定性、可靠性都难以得到充分保证，因此必须对其进行简化［2－3］。但如果模型过于简化，必然导致评估结果不切实际，评估失去意义。本文考虑带未建模动态 (即带未知模型误差）系统的自适应Kalman滤波问题，相应的自适应Kalman滤波器叫做鲁棒Kalman滤波器。采用改进滤波器性能的虚拟噪声补偿技术，通过引入带未知时变均值和方差阵的虚拟白噪声来补偿猎扫雷作战数学模型建立过程中简化带来的未知模型误差，对猎扫雷作战过程建模，并采用相应的Kalrmn滤波器对作战效果进行评估。

1 基于鲁棒Kalman滤波的猎扫雷作战过程建模

根据评估方法的不同，对猎扫雷作战过程建立不同的数学模型。统计类评估技术从概率统计的角度，通过对观测数据的处理，获得评估对象的估计值。在这类技术中，必须对系统建立随机模型，以便对观测数据进行处理。文献 ［1］建立了如下猎扫雷作战过程数学模型:

然而，猎扫雷作战过程中需要考虑的因素很多，涉及的每个数据都多少存在误差。上述模型在采用最优Kalman滤波器进行作战效果评估时，虽然计算方便，但由于建模过程的简化，直接导致评估结果由最优退化为次优。最优Kalman滤波器要求精确已知系统的模型 (包括噪声统计），然而在许多实际应用问题中模型常常近似、带有未知误差［4－5］。这种未知的模型误差叫做未建模动态，它是相对于假设存在系统的一个精确的模型而言的。带未建模动态系统的自适应Kalman滤波器称为鲁棒Kalman滤波器，具有重要的工程应用价值。未建模动态可能来源于:对系统的机理没有完全掌握，或由于简化模型带来的未知模型误差，或由于系统 (过程）的时变性引起模型参数和噪声统计的未知漂移。

考虑在一般状态空间模型中，状态转移阵和观测阵两者均含有未知模型误差的情形，通过引入带未知时变噪声统计的虚拟噪声来补偿模型误差，把问题归结为带未知时变噪声统计系统的自适应Kalman滤波问题，利用时变噪声统计估值器，采用带未建模动态系统的一种统一和通用的鲁棒Kalman滤波技术——虚拟噪声补偿技术对猎扫雷作战过程建模［2］。结合鲁棒Kalman滤波技术，建立改进的猎扫雷作战过程数学模型，过程如下:

参考式(1），猎扫雷作战过程为线性离散随机系统:

假设系统是带未知模型误差系统，即真实系统不是式(2），而是

其中，状态转移阵Φ(t）的误差ΔΦ(t）和观测阵H(t）的误差ΔH(t）未知，但Φ(t）和H(t）已知。因此，即使噪声统计已知，对带模型误差系统进行常规Kalman滤波也会使滤波器性能变坏。为了补偿模型误差，将真实系统改写为:

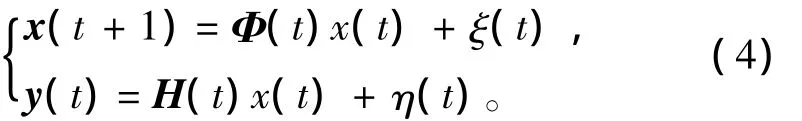
定义虚拟模型噪声 ξ(t）和虚拟观测噪声η(t）为

虚拟噪声ξ(t）补偿了状态模型误差ΔΦ(t）x(t），虚拟噪声η(t）补偿了观测方程误差ΔH(t）x(t）。通常，模型误差项ΔΦ(t），ΔH(t）相对于Φ(t），H(t）而言较小，因此，可近似假设虚拟噪声ξ(t）和η(t）是带未知时变噪声统计的相互独立的白噪声:

于是，对真实系统(3）的滤波问题转化为带未知时变噪声统计系统(4）的自适应Kalman滤波问题。式(4）即为改进的猎扫雷作战过程数学模型。

2 基于鲁棒Kalman滤波的猎扫雷作战效果评估

2.1 鲁棒Kalman滤波器方程组

在卡尔曼滤波技术中，当对模型某一部分了解不深入，存在较大模型误差，或系统模型及误差为时变时，会影响滤波精度，采用鲁棒Kalman滤波器可以补偿未知模型误差。含有未建模动态ΔΦ(t）和ΔH(t）的系统(4）应用虚拟噪声补偿技术有如下Kalman 滤波器［2］:

上述方程组构成了一个卡尔曼滤波器。标准的卡尔曼滤波器有一个重要特点，即状态转移误差方差阵Q(t）在滤波器中不是常数，每次都必须重新计算。由于它受到被估计状态X的影响，使标准卡尔曼滤波器退化为次优。而鲁棒Kalman滤波器状态转移误差方差阵Q(t）和R(t）虽然也是时变的，但虚拟噪声补偿技术补偿了未知模型误差，相对来说有可能会提高估计精度，它的性能如何，必须通过仿真试验和实际应用证明。

2.2 初始条件

为使计算能正常开始，必须提供初始值X0/0和P0/0。通常根据历史经验和实际情况，可以确定比较合理的初始值，从而改善计算结果。但对初始值完全未知时，鲁棒Kalman滤波器仍然可以进行，它可以根据不断取得的观测值，逐渐修正估计结果，并迅速接近真实情况。正因为如此，在工程上经常针对初始值完全未知的情况，对X0/0取0值，对P0/0取一个比较大的值，经过若干步计算后，初始值误差的影响将会消失。

实际搜扫过程中，每当搜扫工具对雷区完成一次作用后，便可得到一个新的观测数据，将这个新的观测数据代入上述方程组，便可由上一个X和P计算出新的X和P，如此反复，X就会逐渐逼近实际状态，从而了解目前雷区内水雷的实际状态。

3 仿真试验结果与分析

情形1:设w(t）的均值q=0和方差Q=0.001已知，取初值(0|0）=［30 0 0］，p=0.3，采用模型 (1）对猎扫雷作战过程建模，可得最优Kalman滤波器0(t|t）。

情形2:取带误差的模型，且取带误差的噪声统计q=0，Q=0.001，取初值为(0|0）=［30 0 0］，p=0.2，采用模型(1）对猎扫雷作战过程建模，可得次优Kalman滤波器s(t|t）。

情形3:取带补偿模型误差系统，采用模型(4）对猎扫雷作战过程建模，可得鲁棒Kalman滤波器(t|t）。其中ξ(t）为带未知时变统计的虚拟白噪声，取ξ(t）的均值和方差的初值为q^=0，Q^=0.001，仍取(0|0）=［30 0 0］，p=0.3，搜扫概率误差在－0.1～0.1之间，且b=0.9。

通过作战过程的仿真，得到1组观测数据和真实数据。将这组观测数据输人到滤波方程中，得到估计值。最后计算出真实状态和估计状态之间的误差。

由于本问题属于小子样估计，相同条件下的仿真结果会呈现随机变化，因此对每组不同条件，均仿真200组，求取其结果的均值和方差。表1列出估计维数为3，观测误差方差R为1.5的条件下，对不同情况进行仿真后所得到的结果。

考虑在防御布雷作战中，水雷定次不会太高。同时，考虑到扫雷概率高的情况下，水雷会很快被扫除，仿真数据会迅速收敛。为了检验评估算法的有效性，故对3种情形采用低概率情况下的3种雷阵进行仿真，结果如下:

1）雷阵1～30枚定次为1次的水雷。

图1 最优滤波、次优滤波和鲁棒Kalman滤波的比较Fig.1 Compare of optimal filter，suboptimal filter and robust Kalman filter

2）雷阵2～10枚定次为1次的水雷+10枚定次为2次的水雷+10枚定次为3次的水雷。

图2 最优滤波、次优滤波和鲁棒Kalman滤波的比较Fig.2 Compare of optimal filter，suboptimal filter and robust Kalman filter

3）雷阵3～30枚定次为1次的水雷+30枚定次为3次的水雷。

图3 最优滤波、次优滤波和鲁棒Kalman滤波的比较Fig.3 Compare of optimal filter，suboptimal filter and robust Kalman filter

3种评估方法对3个雷阵的评估误差均值统计信息如表1所示。

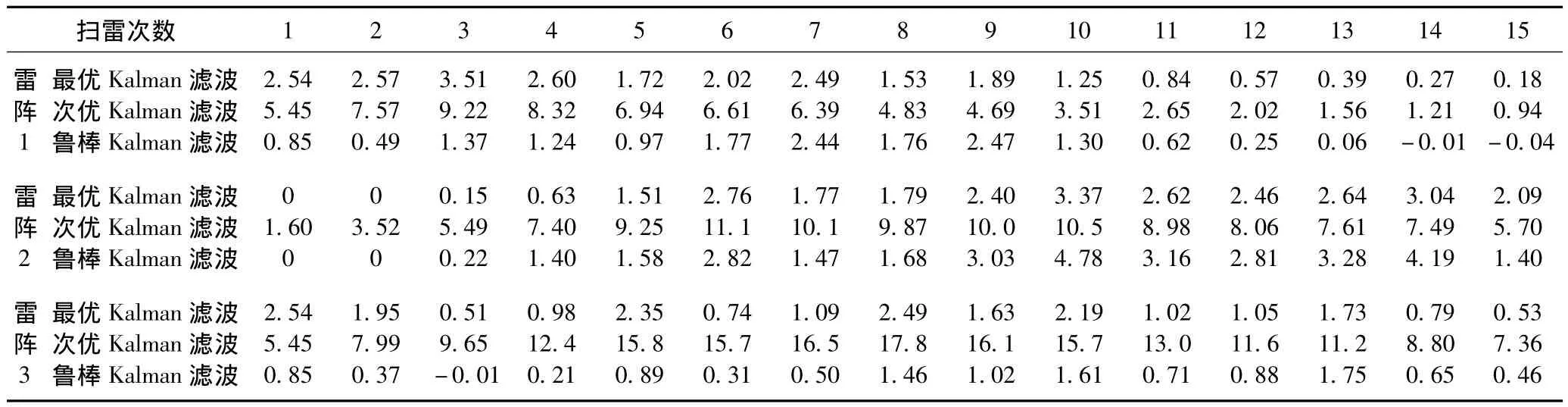
表1 3种典型雷阵的误差均值统计信息表Tab.1 Statistical information ofmean error in three typicalmine obstacle

4 结语

本文在全面考虑猎扫雷作战效果评估需求和已知条件，深入解猎扫雷作战过程本质和具体过程的基础上，结合虚拟噪声补偿技术对猎扫雷作战过程建模，在合理简化的基础上实现更贴近实际的数学抽象，并采用鲁棒Kalman滤波技术对作战效果进行评估。仿真结果表明了该评估方法的有效性，尤其对混布雷阵有很好的评估效果，比最优Kalman滤波器滤波精度更高。对比评估结果可看出，对实际雷数的估计结果，采用鲁棒Kalman滤波技术与实际情况更为接近。

［1］马爱民.猎扫雷作战效果评估与控制［M］.北京:国防工业出版社，2000:70－73.

［2］邓自立.自校正滤波理论及其应用——现代时间序列分析方法［M］.哈尔滨:哈尔滨工业大学出版社，2003:179－181.

［3］周洪光，周玺，夏朗.反水雷武器系统作战效能评估方法初探［J］.水雷战与舰船防护，2010，18(4）:32 －36.

ZHOU Hong-guang，ZHOU Xi，XIA Lang.Preliminary study on the operational efficiency evaluafion methods of MCM weapon system［J］.Mine Warfare and Ship Self-Defence，2010，18(4）:32 －36.

［4］黄贤源，隋立芬，范澎湃.几种最优滤波方法的分析和比较［J］.测绘工程，2007，16(3）:35 －38.

HUANG Xian-yuan，SUI Li-fen，FAN Peng-pai.Analyses and comparisons of some filtermethods［J］.Engineering of Surveying and Mapping，2007，16(3）:35 －38.

［5］李华，李庆民，刘君.一种基于遗传算法的“正向”扫雷效果评估解法［J］.探测与控制学报，2007，29(6）:36－40.

［6］洪星，宋元，马爱民.马尔可夫链用于扫雷作战期望损失评估探讨［J］.兵工学报，2006，27(6）:1132 －1135.

HONG Xing，SONG Yuan，MA Ai-min.The applications of Markov chains to estimating expected casualties of naval mine-sweepin［J］.Actaarmamentarll，2006，27(6）:1132－1135.

Operationalmodeling and effect evaluation ofm ine-hunting and m ine-sweeping based on robust Kalman filter

REN Dong-yan，SUN Ming-tai，ZHOU Li-hui
(Qingdao Branch of Naval Aeronautical and Astronautical University，Qingdao 266041，China）

According to the bad precision of the interweaving mine obstacle in operational effect evaluation ofmine-hunting and mine-sweeping，the operational model of mine-hunting and mine-sweeping was established through using time-varying unmodeled dynamics system.The unknown error of math modeling which was predigested was compensated by fictitious noise compensation technique through introducing the unknown time-varyingmean and variance matrix，and the robust Kalman filter was used for operational effect evaluation.The simulation research testified that the method can effectively improve the performance of Kalman filter and have good operational effect for interweavingmine.The operational process and effectwasmuch more close to the fact.

operational effect evaluation;robust Kalman filter;fictitious noise compensation

TJ01

A

1672－7649(2014）04－0143－04

10.3404/j.issn.1672－7649.2014.04.031

2013－03－12;

2013－04－18

任东彦(1985－），男，博士研究生，主要从事海军兵种及武器系统作战仿真研究。