井筒环空稳态多相流水动力学模型

尹邦堂，李相方，孙宝江，Zhang Hongquan

（1.中国石油大学（华东）石油工程学院；2.中国石油大学（北京）石油工程学院；3.The University of Tulsa）

井筒环空稳态多相流水动力学模型

尹邦堂1，李相方2，孙宝江1，Zhang Hongquan3

（1.中国石油大学（华东）石油工程学院；2.中国石油大学（北京）石油工程学院；3.The University of Tulsa）

基于井筒环空气液两相流流型的分类及特点，建立适合于直井、斜井的井筒环空段塞流、环状流水动力学模型及环空流型过渡准则。基于井筒环空多相流特性，以液膜区域为控制单元，考虑油管膜、套管膜双层液膜的存在及气芯中液滴对质量、动量传递的影响，推导了环空段塞流、环状流质量、动量守恒方程，得到了段塞流与分散泡状流、泡状流及环状流间的流型过渡准则。根据已发表文献中的实验条件，采用本文模型与校正后的圆管模型预测了不同气、液相表观速度下的流型、持液率及压力梯度。结果表明：采用本文模型可以比较准确地预测环空流型、持液率及压降梯度，且预测持液率、压力梯度的准确性优于校正后的圆管模型。图4表6参26

井筒环空；多相流；水动力学模型；稳态；油管膜；套管膜

0 引言

在石油钻采的许多情况下井筒环空中都存在气液两相流动：在钻井过程中如果发生溢流，井筒环空中会出现两相流动；欠平衡钻井过程中也会涉及到井筒环空两相流理论；自喷井在高产量的情况下会通过油套环空以气液混合物的形式进行生产。井筒气液两相流的研究方法可以分为两类：经验模型法[1-3]和机理模型法[4-6]。经验模型法中的环空水力学模型多是在圆管经验公式的基础上采用水力学直径校正的方法建立起来的[7-14]，误差较大。此外，这种方法不能体现环空和圆管在结构上的差异性，通常忽略流型对参数分布的影响，将两相流看成拟单相流，受限于实验条件而不能广泛应用。机理模型法则是考虑流体的形态及性质、环空的结构及流速的影响，针对每种流型分别建立流动方程。20世纪70年代以来，已有较多学者对流型转换模型进行了研究[15-18]，但关于持液率及压降预测的模型较少。油管膜、套管膜双层液膜的存在，使得单元体的受力发生了变化，对流型过渡、持液率、压降等的预测影响较大，在研究环空气液两相流动规律时需要加以考虑。本文基于段塞流的动态变化特征，考虑油管液膜、套管液膜、倾角及气芯中液滴的影响，对井筒环空中段塞流、环状流流型下的水动力学模型及各流型间的过渡准则进行研究，并与前人的气-煤油实验数据[16]进行对比验证。

1 井筒环空两相流流型分类

井筒垂直环空中上升气液两相流流型的分类与圆管中类似，可以分为5种流型[16]（见图1）：泡状流、分散泡状流、段塞流、搅拌流及环状流，其中段塞流及环状流与圆管中流型差别最大。

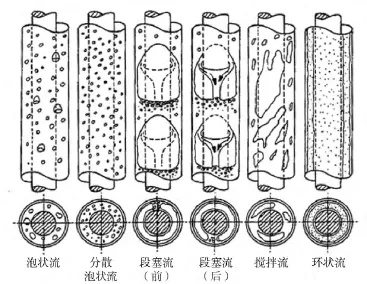
图1 环空中两相流流型分布[16]

环空两相流中的段塞流存在两层液膜，一层是与套管壁（或井壁）接触的套管膜，另一层是与油管壁接触的油管膜。此外，根据Caetano E F[16]的实验观察，Taylor泡不再对称，由于在背部方向存在一个连接油管膜与套管膜的通道，Taylor泡后存在高紊流区域。

环空两相流中的环状流发生在很高的气体流速下，气芯中的气相速度非常高，可能含有液滴，气芯周围是很薄的液膜。由于环空的结构，也存在两种液膜，一种是与油管壁接触的内膜，一种是与套管壁接触的外膜，外膜比内膜厚[16]。

2 环空段塞流水动力学模型

2003年，Zhang H Q等[6,19]基于“段塞流体力学”理论建立了适用于各个流型的统一的圆管水动力学模型（本文称Zhang模型），认为各个流型都可以由段塞流过渡而来：当液塞区域不存在时，段塞流演变为环状流；当液膜区域不存在时，段塞流演变为泡状流或分散泡状流。

本文在段塞流体力学理论基础上，考虑套管膜及与油管膜两层液膜的影响、气液间的传质作用及气芯中液滴的作用，以液膜区域为控制单元建立环空段塞流水动力学模型。

2.1 质量守恒方程

将套管液膜与油管液膜区域作为控制单元（见图2），考虑Taylor泡区域存在液滴，假设液滴速度与液塞运移速度相等，并且控制单元中流体不可压缩。

图2 环空段塞流示意图

对于稳定的段塞流，从液膜底部边界流入的液相质量与从液膜顶部边界流出的液相质量相等，即：

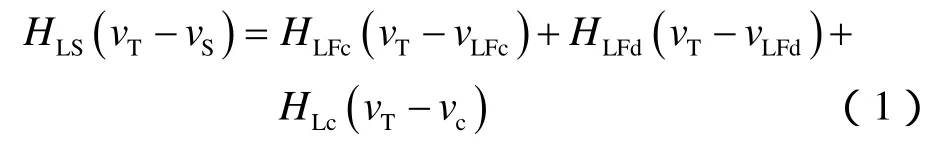
同理，进入液膜的气相质量等于离开液膜的气相质量，即：

由（1）式、（2）式可得：

若Taylor泡通过某个横截面所用的时间为ΔtTB，则ΔtTB内液膜中流动的液相体积为：

若液塞通过相同横截面所用时间为ΔtLS，则ΔtLS内液膜中流动的液相体积为：

在时间ΔtTB+ΔtLS内，段塞单元通过相同横截面时流动的液相体积为：

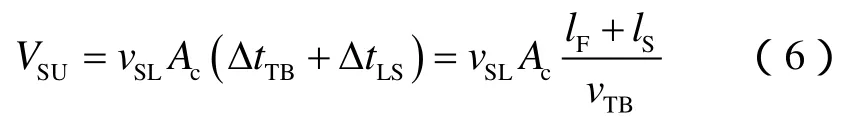
由质量守恒定律可得：

由（4）～（7）式可得段塞单元中液相质量守恒方程：

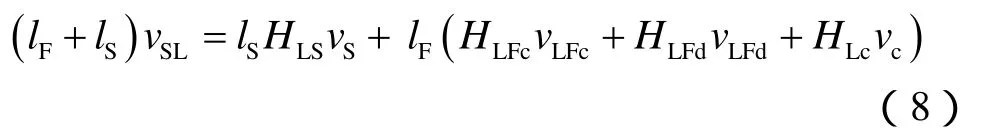
同理，段塞单元中气相质量守恒方程为：

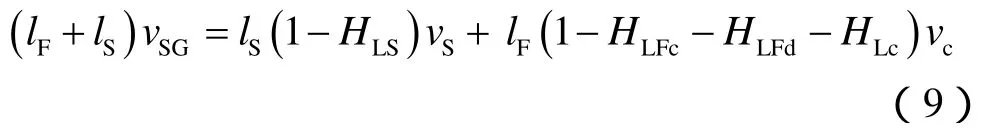
此外，Taylor泡中液滴体积分数[6]可以表示为：

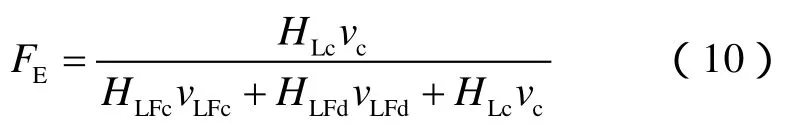
2.2 动量守恒方程

对套管膜进行受力分析（见图3），根据动量守恒定律可得：

（11）式可变换为：

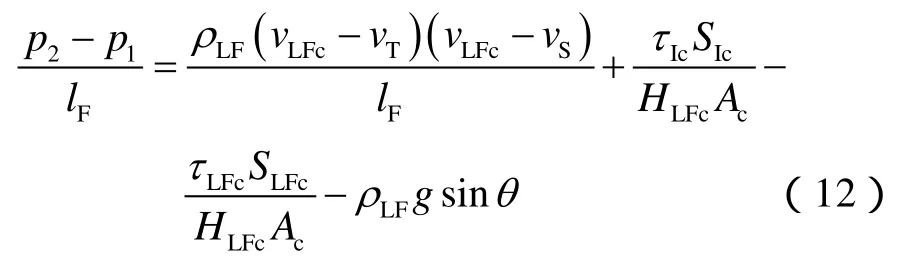
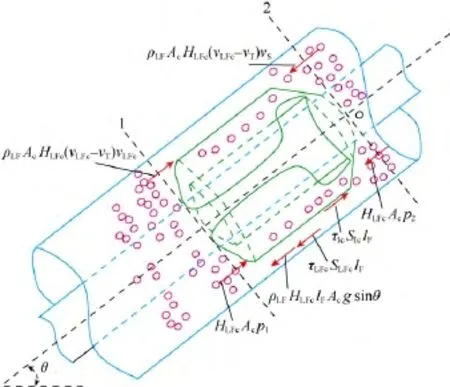
图3 环空段塞流中套管膜受力示意图

同理，对于油管膜：

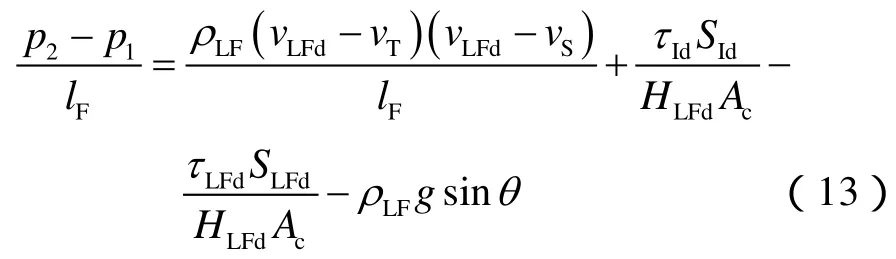
同理，对于Taylor泡：

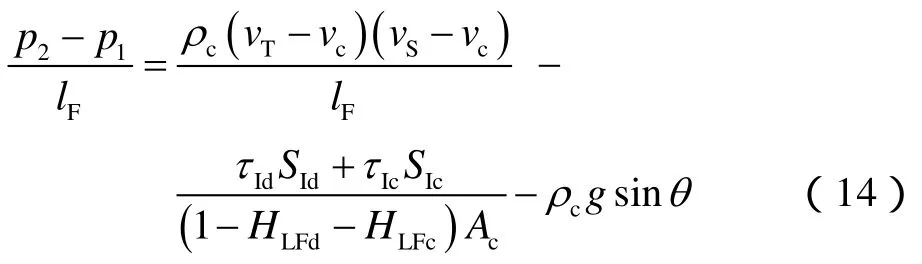
其中

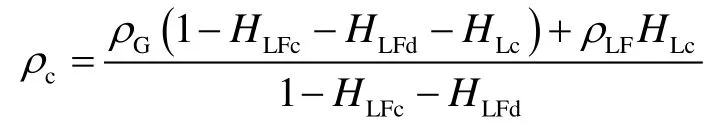
将（12）式、（13）式分别与（14）式联立，可得环空段塞流动量守恒方程：

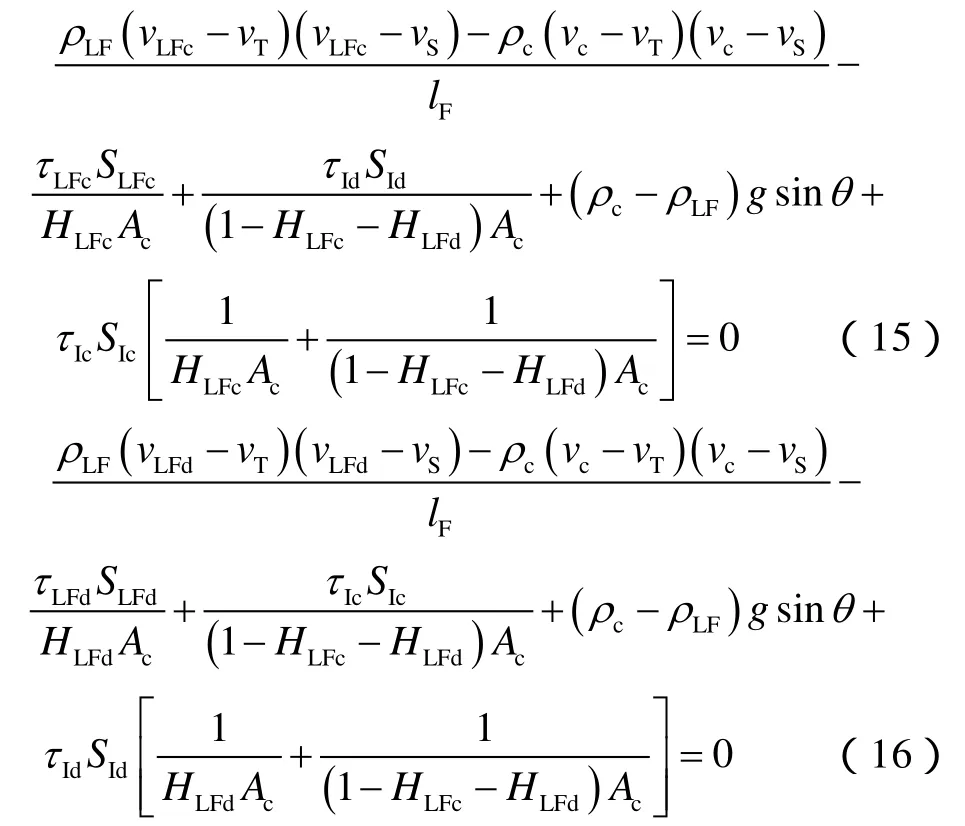
2.3 辅助参数计算方法

①液塞运移速度。Nicklin D J[20]提出液塞运移速度可以表示为混合速度的函数：

（17）式中，CS是稳定段塞的最大速度与平均速度之比，随着流动条件的变化而变化。Zhang H Q等[6]认为层流时该值等于2.0，紊流时该值等于1.3。在过渡区域（Re在2 000～4 000）：

Santos O L A等[21]建立了流体为钻井液时Taylor泡的上升速度模型：

其中

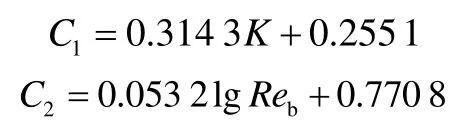
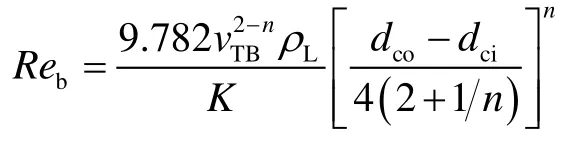
②界面摩擦因子。段塞流中液膜与Taylor泡接触的界面会产生摩擦力，Andritsos N等[22]建立了计算界面摩擦因子的模型，本文采用该模型计算套管膜、油管膜与Taylor泡的界面摩擦因子。

对于套管膜与Taylor泡接触面：

对于油管膜与Taylor泡接触面：

③壁面剪切力。环空段塞流动量守恒方程中的壁面剪切力计算方法如下：

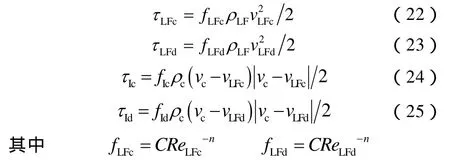
采用水力学当量直径方法，套管膜、油管膜与Taylor泡界面的雷诺数可以表示为：

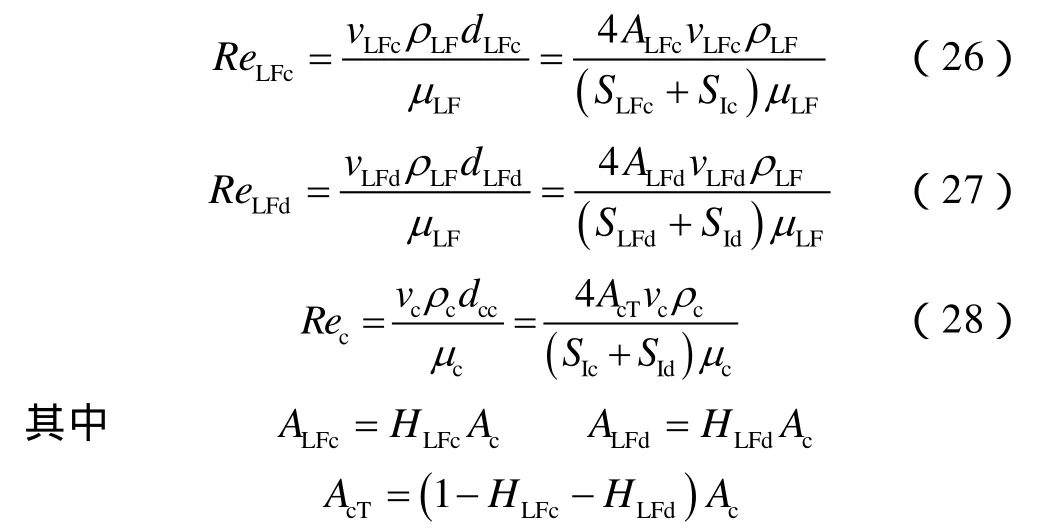
④管壁及界面的周长。当气体流速较高或者倾斜角较大时，管壁处液膜厚度就会增加，导致管壁与液膜界面周长的增大，可以采用Grolman校正公式[23]计算管壁润湿分数：⑤套管膜与油管膜持液率之比。 采用Caetano E F[16]建立的环空环状流持液率模型及套管膜、油管膜厚度比模型计算套管膜与油管膜持液率之比：

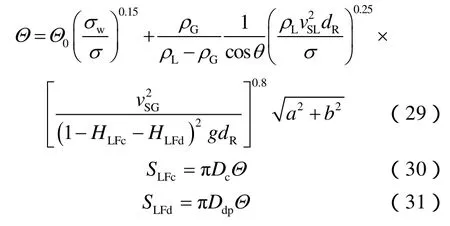
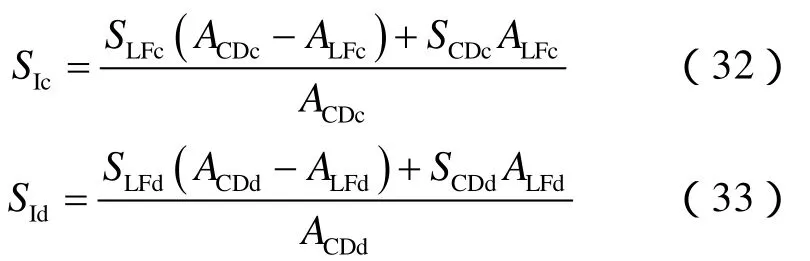
由于δc、δdp与套管、油管直径相比小很多，则（34）式可简化为：

⑥压力梯度。整个段塞单元的平均压力梯度可以表示为：

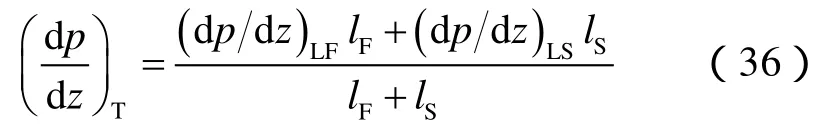
液膜区及液塞区的压力梯度均包含重力项、加速度项及摩擦阻力项。摩擦阻力项均包括3部分：套管膜阻力、油管膜阻力及Taylor泡阻力。

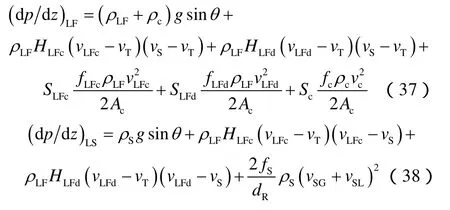
3 环空环状流水动力学模型

环空中的环状流（见图4）可以等效为高速流动的气芯被套管膜、油管膜包围，同时气芯中含有一些小液滴。

3.1 质量守恒方程

由于液相包含套管膜、油管膜及气芯中液滴3部分，其质量守恒方程为：

由于气相仅存在于气芯中，其质量守恒方程为：

假设气芯中气液均匀分布，则：

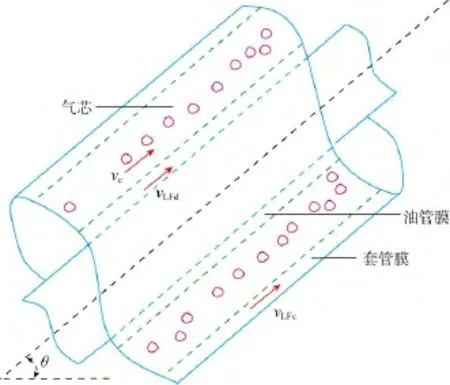
图4 环空环状流示意图

3.2 动量守恒方程

（15）式、（16）式等号左边第1项均表示液塞区与液膜区的动量交换，当段塞流过渡到环状流时，不再存在液塞区，即液塞区与液膜区的动量交换变为零，也就是（15）式、（16）式等号左边第1项变为零，即环空环状流下动量守恒方程为：

3.3 辅助参数计算方法

周长、水力学直径、横截面积、套管膜与油管膜持液率之比等参数的计算方法参照环空段塞流。

①界面摩擦因子。本文采用Ambrosini W等[24]修正的Asali模型计算套管膜、油管膜与气芯的界面摩擦因子。

套管膜与气芯的界面摩擦因子为：

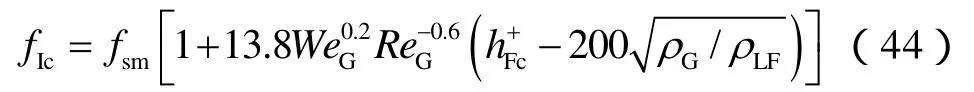
油管膜与气芯的界面摩擦因子为：

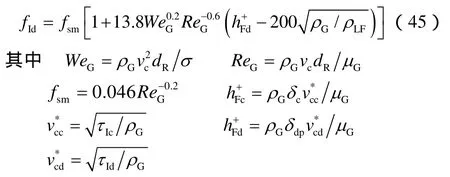
②管壁摩擦因子。Caetano E F[16]基于连续性方程、动量方程及Fanning方程推导了环空中管壁摩擦因子方程。

对于层流：

对于紊流：

4 环空流型过渡准则

基于不同流型的形成机理，在前人研究成果的基础上建立环空流型过渡准则。

4.1 分散泡状流到段塞流的过渡

当vSG大于0.1 m/s时，采用Zhang H Q[19]建立的分散泡状流到段塞流的过渡模型，并采用水力学当量直径的方法进行校正：

4.2 泡状流到段塞流的过渡

当环空中气体流速较低时，离散的气泡不会发生碰撞及合并，气泡直线上升。当气体流速较高时，气泡开始变大，达到临界尺寸时气泡开始变形并以Z型路线运动，然后开始碰撞、合并，形成球形泡，与段塞流中的Taylor泡类似。这时就会发生向段塞流的过渡。在纯水中，Taitel Y等[26]认为当含气率达到25%时，泡状流会向段塞流发生过渡，当气泡间的距离是气泡半径的一半时就会发生急剧的合并。Caetano E F[16]通过实验研究认为，当环空中含气率为20%时，会发生泡状流到段塞流的过渡。所以，泡状流到段塞流的过渡准则为：

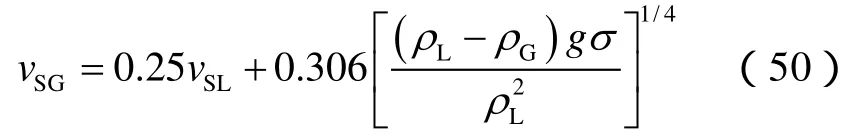
4.3 段塞流到环状流的过渡

当环空中的气体流速很高时会发生段塞流到环状流的过渡。液相以液膜的形式沿着管壁向上运动，同时在气芯中还可能以小液滴的形式存在。当段塞流中的液膜变得无限长时，就会发生段塞流向环状流的过渡，使得液塞与液膜间的动量交换变为零。基于Zhang H Q[6]建立的段塞流到环状流的过渡模型得到环空段塞流到环状流的过渡准则：

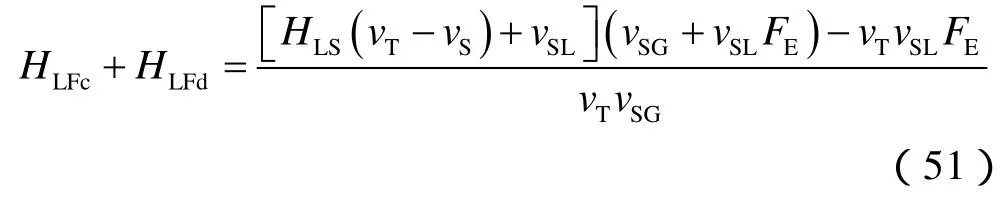
5 模型验证

Caetano E F[16]在外径76.2 mm、内径42.2 mm的环空中，对不同温度、压力、表观速度下的气-煤油两相流流型、持液率及压降梯度进行了实验研究。根据Caetano E F[16]的实验条件，利用本文建立的环空段塞流、环状流水动力学模型及经过当量直径校正后的Zhang模型[6]，对不同液相表观速度、气相表观速度下的流型、持液率及压降梯度进行预测，并与实验结果[16]进行对比。

模型求解的具体步骤（以环空段塞流为例）如下：①输入基本参数，先求解vT、lS和FE，估算HLS，给定lF的初值；②基于辅助参数计算方法，求解质量守恒方程，得到VLFc、VLFd、Vc、HLFc、HLFd和HLc；③计算SLFc、SLFd、SIc、SId、fLFc、fLFd、fIc和fId；④计算摩阻和HLS；⑤利用动量守恒方程，求解lF；⑥判断lF是否满足迭代精度，若满足，求解结束，若不满足，返回①重新开始。

表1、表2分别为段塞流、环状流下采用本文模型和校正后的Zhang模型预测的流型及与实验结果的对比，可以看出：采用本文建立的模型可以比较准确地预测环空流型，且对段塞流的预测比对环状流的预测更准确。

表3—表6分别为段塞流、环状流下采用本文模型和校正后的Zhang模型预测的持液率、压力梯度及与实验结果的对比。可以看出：采用本文模型预测的环空段塞流下持液率、压力梯度与实验结果相比误差均在15%以内，预测的环空环状流下持液率、压力梯度与实验结果相比误差均在25%以内；采用Zhang模型预测的环空段塞流及环状流下持液率、压力梯度与实验结果相比平均误差在50%左右，且在液相相对速度较大、气相相对速度较小时误差较小，在液相相对速度较小、气相相对速度较大时误差很大。因此，采用本文建立的环空段塞流、环状流水力学模型可以比较准确地预测持液率、压力梯度，且准确性优于采用当量直径方法校正后的Zhang模型。

表1 段塞流下流型的模型预测结果与实验结果对比

表2 环状流下流型的模型预测结果与实验结果对比

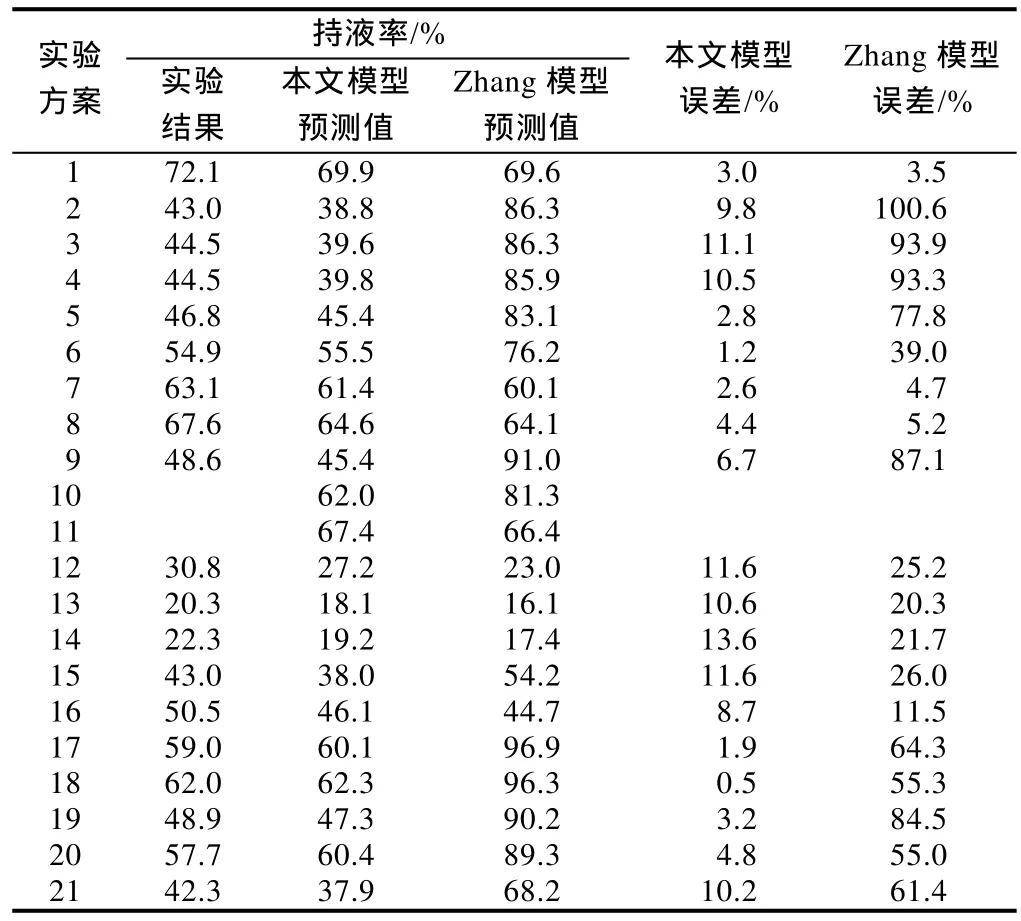
表3 段塞流下持液率的模型预测结果与实验结果对比

表4 段塞流下压力梯度的模型预测结果与实验结果对比

表5 环状流下持液率的模型预测结果与实验结果对比

表6 环状流下压力梯度的模型预测结果与实验结果对比

6 结论

分析了井筒环空气液两相流流型的分类及特点，并与圆管气液两相流流型进行了对比。基于段塞流体力学理论，以液膜区域为控制单元，考虑环空段塞流下油管膜与套管膜的影响及气芯中液滴的影响，建立了适合于直井、斜井的井筒环空段塞流、环状流水动力学模型，推导了质量守恒方程和动量守恒方程，并给出了辅助参数计算方法。考虑环空中气液两相流流动特点和环空结构对流型过渡的影响，建立了环空流型过渡准则。

利用已发表文献中实验数据对本文建立的环空段塞流、环状流水动力学模型进行了验证，并与经过当量直径校正后的圆管模型进行了对比。结果表明：与实验结果相比，本文模型对流型的预测比较准确，段塞流模型对持液率及压降梯度的预测误差均在15%以内，环状流模型对持液率及压降梯度的预测误差均在25%以内，而校正后的圆管模型对段塞流及环状流下持液率、压降梯度的平均预测误差约为50%。

符号注释：

HLFc——套管膜持液率，%；vLFc——套管膜流动速度，m/s；vT——液塞运移速度，m/s；HLFd——油管膜持液率，%；vLFd——油管膜流动速度，m/s；HLc——Taylor泡持液率，%；vc——Taylor泡流动速度，m/s；HLS——液塞持液率，%；vS——液塞流动速度，m/s；ΔtTB，ΔtLS——Taylor泡、液塞通过某个横截面所用的时间，s；ρLF——液膜密度，kg/m3；Ac——井筒环空横截面积，m2；lU——段塞单元长度，m；lF——液膜区长度，m；lS——液塞区长度，m；vTB——Taylor泡的上升速度，m/s；VLF——ΔtTB内液膜中流动的液相体积，m3；VLS——ΔtLS内液膜中流动的液相体积，m3；VSU——ΔtTB+ΔtLS内液膜中流动的液相体积，m3；vSL——液相表观速度，m/s；vSG——气相表观速度，m/s；FE——Taylor泡区域中液滴体积分数，%；p1，p2——段塞单元入口端、出口端压力，Pa；τIc——套管膜与Taylor泡接触界面的剪切力，Pa；SIc——套管膜与Taylor泡接触界面的湿周，m；τLFc——套管壁与套管膜接触界面的剪切力，Pa；SLFc——套管壁湿周，m；τId——油管膜与Taylor泡接触界面的剪切力，Pa；SId——油管膜与Taylor泡接触界面的湿周，m；τLFd——油管壁与油管膜接触界面的剪切力，Pa；SLFd——油管壁湿周，m；g——重力加速度，9.8 m/s2；θ——井筒倾斜角，（°）；ρc——Taylor泡区域当量密度，kg/m3；ρG——Taylor泡区域气相密度，kg/m3；ρL——Taylor泡区域液相密度，kg/m3；CS——稳定段塞的最大速度与平均速度之比；Re——雷诺数；dc——气泡直径，m；C1——考虑环空结构的影响系数；K——钻井液稠度系数，Pa·sn；C2——考虑钻井液非牛顿性质的影响系数；Reb——气泡雷诺数；n——钻井液流动特性指数；dco——环空外径，m；dci——环空内径，m；fc——Taylor泡的界面摩擦因子；fIc——套管膜与Taylor泡接触面的摩擦因子；fId——油管膜与Taylor泡接触面的摩擦因子；δc，δdp——套管膜和油管膜厚度，m；ρG0——大气压下的气体密度，kg/m3；fLFc——套管壁与套管膜接触面的摩擦因子；fLFd——油管壁与油管膜接触面的摩擦因子；ReLFc——套管膜与Taylor泡界面的雷诺数；C——局部变量；dLFc——套管膜与Taylor泡界面直径，m；μLF——液膜黏度，mPa·s；ReLFd——油管膜与Taylor泡界面的雷诺数；dLFd——油管膜与Taylor泡界面直径，m；Rec——Taylor泡雷诺数；dcc——Taylor泡直径，m；μc——Taylor泡黏度，mPa·s；ALFc——套管膜横截面积，m2；ALFd——油管膜横截面积，m2；AcT——Taylor泡横截面积，m2；Θ——管壁润湿分数；Θ0——平面的最小润湿分数；σ——液膜的表面张力，N；σw——水的表面张力，N；dR——环空当量直径，m；a，b——系数；Dc——套管直径，m；Ddp——油管直径，m；ACDc——套管膜的湿壁和湿壁对应的弦包围的横截面积，m2；ACDd——油管膜的湿壁和湿壁对应的弦包围的横截面积，m2；SCDc——套管膜的湿壁和湿壁对应的弦包围的湿周，m；SCDd——油管膜的湿壁和湿壁对应的弦包围的湿周，m；R——环空内径与外径的比值；(dp/dz)T——整个段塞单元的压力梯度，Pa/m；(dp/dz)LF——液膜区压力梯度，Pa/m；(dp/dz)LS——液塞区压力梯度，Pa/m；WeG——韦伯数；ReG——气相雷诺数；μG——气相黏度，mPa·s； fsm——光滑管的摩擦因子；——套管液膜无量纲厚度；——油管液膜无量纲厚度；fCA——环空中管壁摩擦因子；FCA——环空中摩擦几何参数；Tsm——管壁与液塞、液膜间动量交换量之和；fS——液塞与管壁的摩擦因子；ρS——液塞密度，kg/m3。

[1]Hagedorn A R,Brown K E.Experimental study of pressure gradients occurring during continuous two-phase flow in small diameter vertical conduits[J].Journal of Petroleum Technology,1965,17(4):475-484.

[2]Beggs H D,Brill J P.A study of two-phase flow in inclined pipes[J].Journal of Petroleum Technology,1973,25(5):607-617.

[3]Hasan A R,Kabir C S.A study of multiphase flow behavior in vertical wells[J].SPE Production Engineering Journal,1988,3(2):263-272.

[4]Petalas N,Aziz K.A mechanistic model for multiphase flow in pipes[J].Journal of Canadian Petroleum Technology,2000,39(6):43-55.

[5]Kaya A S,Sarica C,Brill J P.Mechanistic modeling of two-phase flow in deviated wells[J].SPE Production and Facilities,2001,16(3):156-165.

[6]Zhang H Q,Wang Q,Sarica C,et al.Unified model for gas-liquid pipe flow via slug dynamics-part 1:Model development[J].Journal of Energy Resources Technology,2003,125(4):266-273.

[7]Nickens H V.A dynamic computer model of kick well[J].SPE Drilling Engineering,1987,2(2):158-173.

[8]Rommetveit R,Fjelde K K,Aas B.HPHT well control:An integrated approach[R].OTC 15322,2003.

[9]李相方.井涌期间气液两相流动规律研究[D].北京:中国石油大学(北京),1993.Li Xiangfang.Gas-liquid two phase flow during well kicks[D].Beijing:China University of Petroleum(Beijing),1993.

[10]任美鹏,李相方,徐大融,等.钻井气液两相流体溢流与分布特征研究[J].工程热物理学报,2012,33(12):2120-2125.Ren Meipeng,Li Xiangfang,Xu Darong,et al.Research of kick and distribution features of gas-liquid two phase flow during drilling[J].Journal of Engineering Thermophysics,2012,33(12):2120-2125.

[11]Gao Y H,Sun B J,Xiang C S,et al.Gas hydrate problems during deep water gas well test[R].Shenzhen:SUTTC,2012.

[12]王志远.含天然气水合物相变的环空多相流流型转化机制研究[D].东营:中国石油大学(华东),2009.Wang Zhiyuan.Study on annular multiphase flow pattern transition mechanism considering gas hydrate phase transition[D].Dongying:China University of Petroleum (Huadong),2009.

[13]杨进,唐海雄,刘正礼,等.深水油气井套管环空压力预测模型[J].石油勘探与开发,2013,40(5):616-619.Yang Jin,Tang Haixiong,Liu Zhengli,et al.Prediction model of casing annulus pressure for deepwater well drilling and completion operation[J].Petroleum Exploration and Development,2013,40(5):616-619.

[14]Sun B J,Gong P B,Wang Z Y.Simulation of gas kick with high H2S content in deep well[J].Journal of Hydrodynamics,2013,25(2):264-273.

[15]Sadatomi M,Sato Y,Saruwatari S.Two-phase flow in vertical noncircular channels[J].International Journal of Multiphase Flow,1982,8(6):641-655.

[16]Caetano E F.Upward vertical two-phase flow through an annulus[D].Tulsa:The University of Tulsa,1986.

[17]Caetano E F,Shoham O,Brill J P.Upward vertical two-phase flow through an annulus:part Ⅰ:Single phase friction factor,Taylor bubble velocity and flow pattern prediction[J].Journal of Energy Resources Technology,1992,114:1-13.

[18]Caetano E F,Shoham O,Brill J P.Upward vertical two-phase flow through an annulus:part Ⅱ:Modeling bubble,slug and annulus flow[J].Journal of Energy Resources Technology,1992,114:14-30.

[19]Zhang H Q,Wang Q,Sarica C.Unified model for gas-liquid pipe flow via slug dynamics-part 2:Model validation[J].Journal of Energy Resources Technology,2003,125(4):274-283.

[20]Nicklin D J.Two-phase bubble flow[J].Chemical Engineering Science,1962,17(9):693-702.

[21]Santos O L A,Azar J J.A study on gas migration in stagnant non-Newtonian fluids[R].SPE 39109,1997.

[22]Andritsos N,Hanratty T J.In fl uence of interfacial waves in strati fi ed gas-liquid flows[J].AIChE Journal,1987,33(3):444-454.

[23]Grolman E.Gas-liquid flow with low liquid loading in slightly inclined pipes[D].The Netherlands:University of Amsterdam,1994.

[24]Ambrosini W,Andreussi P,Azzopardi B J.A physically based correlations for drop size in annular flow[J].International Journal of Multiphase Flow,1991,17(4):497-507.

[25]Barnea D.A unified model for predicting flow-pattern transition for the whole range of pipe inclinations[J].International Journal of Multiphase Flow,1987,13(1):1-12.

[26]Taitel Y,Barnea D,Dukler A E.Modeling flow pattern transition for steady upward gas-liquid flow in vertical tubes[J].AIChE Journal,1980,26(3):345-354.

（编辑 胡苇玮 绘图 刘方方）

Hydraulic model of steady state multiphase flow in wellbore annuli

Yin Bangtang1,Li Xiangfang2,Sun Baojiang1,Zhang Hongquan3
(1.School of Petroleum Engineering,China University of Petroleum (Huadong),Qingdao 266580,China;2.College of Petroleum Engineering,China University of Petroleum,Beijing 102249,China;3.The University of Tulsa,Tulsa 74104,United States of America)

Based on the classification and flow behaviors of two phase flow in wellbore annuli,the hydraulic models for slug flow and annular flow in annuli for vertical or inclined wells were established,and the flow regime transition criteria were also obtained.Based on the flow behavior research of multiphase flow in wellbore annuli,the liquid film zone was used as the control volume,and the effect of the tubing liquid film,casing liquid film and the droplets in gas core area on the mass and momentum transfers were considered.The mass and momentum conservation equations of slug and annular flows were obtained.Then the evaluation criterion of flow pattern transitions were established,including dispersed flow to slug flow,bubble flow to slug flow and slug flow to annular flow.The model prediction results were compared under the experimental conditions from the previous literatures.The predictions of flow pattern,liquid holdup and pressure gradient were compared between the new model and the pipe flow model modified by using the hydraulic diameter.The results show that the flow pattern,liquid holdup and pressure gradient can be predicted by the new model more accurately,and the prediction of liquid holdup and pressure gradient are better.

wellbore annuli;multiphase flow;hydraulic model;steady state;tubing liquid film;casing liquid film

国家科技重大专项（2011ZX05056-001-03；2011ZX05056-001-04）；国家建设高水平大学公派联合培养博士研究生项目（2011644002）；中央高校基本科研业务费专项资金（14CXOZ167A）

TE21;P744.4

：A

1000-0747(2014)03-0359-08

10.11698/PED.2014.03.13

尹邦堂（1985-），男，山东青州人，博士，中国石油大学（华东）石油工程学院讲师，主要从事井筒多相流理论及应用、深水钻井井控工艺技术、深水油气井井筒流动保障技术等方面的研究工作。地址：山东省青岛经济技术开发区长江西路66号，中国石油大学（华东）石油工程学院，邮政编码：266580。E-mail：yinbangtang@163.com

2013-11-24

2014-04-30