空间圆弧轨迹的井斜演化规律及控制模式

刘修善，苏义脑

（1.中国石化石油工程技术研究院；2.中国石油集团钻井工程技术研究院）

空间圆弧轨迹的井斜演化规律及控制模式

刘修善1，苏义脑2

（1.中国石化石油工程技术研究院；2.中国石油集团钻井工程技术研究院）

建立空间圆弧轨迹的井斜方程，得到空间圆弧轨迹所在斜平面姿态、空间圆弧轨迹井斜角极值等求解方法，揭示空间圆弧轨迹的井斜演化规律及控制模式。可分别由正演模型和反演模型计算出空间圆弧轨迹上任一点的井斜角和方位角、斜平面姿态的倾斜角和倾斜方位角以及轨迹井斜角极值点参数，正演模型和反演模型的计算结果完全相同。空间圆弧轨迹或其趋势线存在井斜角极值点，极小和极大井斜角点的井眼轨迹切线分别指向所在斜平面的下倾和上倾方向，两个极值点的弯曲角和方位角均相差180°。斜平面姿态参数、井斜角极值点参数与井段始点的井斜角和工具面角有关，与井段长度无关。对于空间圆弧轨迹，斜面倾角模式存在二义性，应使用工具面角或定向方位角控制模式。图3表4参20

钻井理论；定向钻井；井眼轨迹；井斜演化

0 引言

目前，空间圆弧模型被广泛用于设计、监测和控制井眼轨迹，并被纳入石油天然气行业标准[1-2]。早期的有关研究主要集中于实钻轨迹的测斜数据计算，以计算井眼轨迹的坐标参数为研究重点[3-5]。随着地质条件日趋复杂和钻井技术不断进步，钻探了各种类型的三维定向井，因此基于空间圆弧模型发展形成了一系列三维井眼轨迹设计方法[6-13]。同时，在空间圆弧轨迹的模型化研究方面也取得了显著的进展[14-17]。

空间圆弧轨迹是位于空间斜平面内的圆弧，其井眼曲率保持不变且井眼挠率为零，可被视为1条二维曲线，也是最简单的井眼轨迹模型。然而，空间圆弧轨迹在垂直剖面图和水平投影图上都不是圆弧，且工具面角沿井深变化，给理论计算和施工工艺设计都带来了一些困难。2006年，笔者发现用于扭方位设计的计算公式会出现异常结果[18]，随后韩志勇通过研究井斜角的变化规律及特征解释了这种现象[19]，还提出了用于控制空间圆弧轨迹的斜面倾角模式[20]。本文研究空间圆弧轨迹的井斜角极值、所在斜平面姿态以及两者之间的对应关系等问题，旨在厘清空间圆弧轨迹的井斜演化规律及控制模式，为井眼轨迹设计、监测与控制提供参考。

1 空间圆弧轨迹井斜方程

井眼轨迹模型以井段为研究对象，将其假设为具有明确物理意义和几何意义的特定曲线，既适用于设计轨道也适用于实钻轨迹。在研究井眼轨迹模型时，井段始点的轨迹参数通常为已知数据，如果给定井段的轨迹特征参数，则可以计算出井段终点的基本轨迹参数（井深、井斜角和方位角）；反之，若给定井段终点的基本轨迹参数，也可以计算出井段的轨迹特征参数。将这两种情况的井眼轨迹模型分别称之为正演模型和反演模型。显然，正反演模型的已知条件不同，但两者之间可以相互换算和验证，并且都可以计算井段的坐标增量。

空间圆弧轨迹（见图1）的特征参数是井段的井眼曲率κ（或曲率半径R）和井段始点的工具面角ωA（本文称初始工具面角），前者决定了井眼轨迹的形状，后者决定了井眼轨迹的姿态[17]。

图1 空间圆弧轨迹及所在斜平面

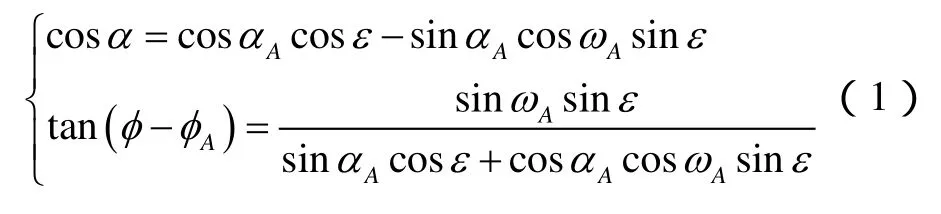
可见，正演模型和反演模型都将任一井深处的井斜角α和方位角φ表示成弯曲角ε的函数。考虑到弯曲角与井段长度的关系，井斜角和方位角也是井段长度的函数。应用（1）式、（2）式可计算出任一井深处的井斜角和方位角，且既适用于内插计算也适用于外插计算[17]。

2 空间斜平面姿态

空间圆弧轨迹是位于空间斜平面内的圆弧，空间圆弧轨迹的姿态决定了其所在斜平面的姿态。空间斜平面的姿态可用倾斜角β和倾斜方位角ψ表征[20]，倾斜角是指空间斜平面与垂直方向的夹角，倾斜方位角是指空间斜平面的倾斜方向投影到水平面上后与正北方向的夹角（见图1）。

根据空间圆弧轨迹与空间斜平面之间的约束关系，应用空间解析几何和向量分析原理，可以分别得到基于正演模型和反演模型的斜平面姿态参数：

倾斜角β和倾斜方位角ψ都存在下倾方向和上倾方向的两个值（见图1）。计算出的两个倾斜角中数值较小者为下倾方向的倾斜角，相应的倾斜方位角为下倾方向，数值较大者为上倾方向的倾斜角，相应的倾斜方位角为上倾方向。此外，倾斜角和倾斜方位角的值域分别为[0°，180°]和[0°，360°]，而反正弦函数和反正切函数的主值区间都是[−90°，90°]，所以还应将计算结果换算到相应的值域范围内。

3 井斜角极值

上述研究结果表明：在空间圆弧轨迹的形状和姿态都确定的条件下，井斜角随井深的变化规律并非单调增加或减小，而是呈三角函数关系，说明井斜角可能存在极值，例如，稳斜扭方位时只是扭方位井段的始点和终点井斜角相等，其间往往是增斜和降斜井段共存，且增斜与降斜的量值相等，所以二者相互抵消后便实现了稳斜效果[18-19]。

应用极值理论，基于井斜角方程可得到井斜角极值。对于正演模型：

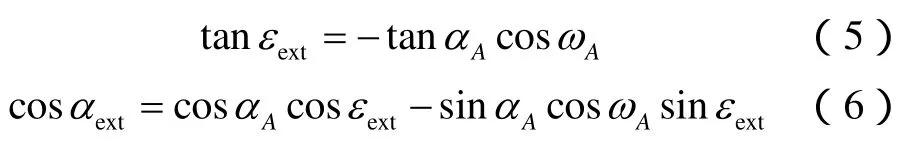
对于反演模型：

为判别井斜角极值是极小值还是极大值，对于正演模型，令：

对于反演模型，令：

q为正值时，αext为极小井斜角；q为负值时，αext为极大井斜角。

4 井斜演化规律

圆弧是圆的一部分，把1段空间圆弧轨迹向两侧延伸将得到1个圆形，这样的圆形有4个特殊点（见图2）[19]。a点和c点分别为圆形轨迹的最高点和最低点，在这两点处圆形轨迹的切线都指向水平方向，因此井斜角均为90°。b点和d点都是增降斜的转折点，但是其两侧的井斜变化趋势相反。b点和d点是井斜角的极值点，其井斜角分别为极小值αmin和极大值αmax。可以证明，所以圆形轨迹的极小井斜角和极大井斜角分别等于斜平面下倾和上倾方向的倾斜角。事实上，b点和d点处的圆形轨迹切线分别指向斜平面的下倾和上倾方向，在这两点处圆形轨迹的方位角也分别等于斜平面下倾和上倾方向的倾斜方位角。

图2 井斜角变化规律

上述4个特殊点将圆形轨迹分为4个区间[19]，若从a点开始沿顺时针方向行进，则井斜角的变化规律为：①第Ⅰ区间（a→b）为降斜，井斜角从αa=90°降到αb=αmin；②第Ⅱ区间（b→c）为增斜，井斜角从αb=αmin增到αc=90°；③第Ⅲ区间（c→d）为增斜，井斜角从αc=90°增到αd=αmax；④第Ⅳ区间（d→a）为降斜，井斜角从αd=αmax降到αa=90°。当斜平面为垂直方向平面时，αmin=0°，αmax=180°；当斜平面为水平面时，αmin= αmax=90°，此时任一点的井斜角均为90°。

5 轨迹控制模式

空间圆弧轨迹是最简单的数学曲线，其显著特征是井眼曲率为常数。但空间圆弧轨迹的工具面角是沿井深变化的，尽管可以设计和计算出空间圆弧轨迹上每一点的工具面角[17]，但目前还没有相应的工艺技术能使工具面角沿井深连续变化。为解决这个现场施工技术难题，韩志勇[20]提出了斜面倾角模式，即采用斜平面的倾斜角和倾斜方位角作为空间圆弧轨迹的控制参数。但是，这种方法存在二义性（见图3），无法唯一确定空间圆弧轨迹的姿态。

图3 斜面倾角模式的二义性

由（3）式可知：空间圆弧轨迹所在斜平面的姿态参数取决于井段始点的井斜角和工具面角。在始点井斜角相同的条件下，初始工具面角相差180°的两个空间圆弧轨迹具有相同的斜平面姿态参数（见图3）。在斜平面倾斜角和倾斜方位角确定的条件下，从某点C开始既可能钻出轨迹Γ1也可能钻出轨迹Γ2，而轨迹Γ1和轨迹Γ2却是背道而驰的。因此，对于空间圆弧轨迹仍推荐使用工具面角或定向方位角控制模式[17]，并且在定向钻进施工过程中要及时监控工具面角或定向方位角。通常，如果利用MWD（随钻测量）等仪器每钻进1个单根监控1次或多次工具面角，基本能够满足井眼轨迹控制的工程需求。

6 实例分析

假设某空间圆弧井段的井眼曲率为12°/30 m，始点井斜角αA为30°、工具面角ωA为60°，则由正演模型计算可得：①斜平面姿态参数。下倾和上倾方向倾斜角分别为25.659°和154.341°，下倾和上倾方向倾斜方位角与井段始点方位角之差分别为−33.690°和146.310°。②井斜角极值点参数。井眼轨迹的极小/极大井斜角（25.659°/154.341°）位于井段长度−40.255 m/409.745 m、弯曲角−16.102°/163.898°处，极小/极大井斜角点的方位角与始点方位角之差为−33.690°/ 146.310°。

为了验证正反演模型的计算结果，首先用正演模型计算出不同井段长度条件下的终点轨迹参数，再用反演模型求取斜平面姿态参数（见表1）和井斜角极值点参数（见表2）。在保持始点井斜角和井眼曲率不变的条件下，分别取始点工具面角为30°、60°、120°、240°、300°和320°，重复上述方法，计算结果见表3、表4。

表1 初始工具面角为60°时的斜平面姿态参数

表2 初始工具面角为60°时的井斜角极值点参数

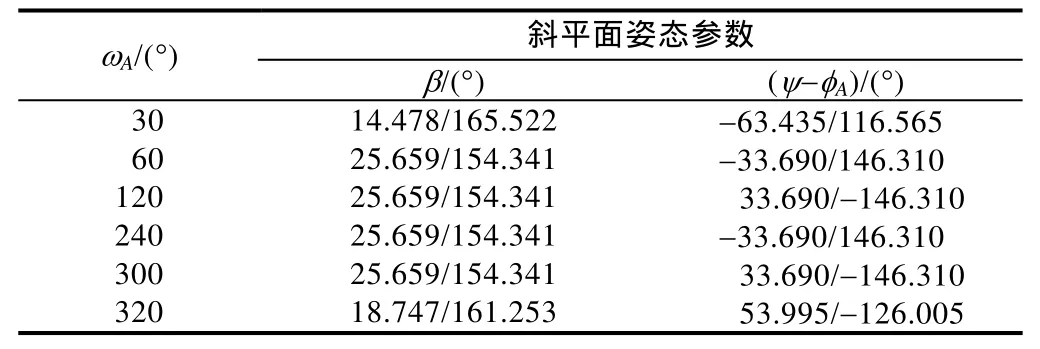
表3 不同初始工具面角下斜平面姿态参数

表4 不同初始工具面角下井斜角极值点参数

由表1—表4可知：①利用正演模型和反演模型求得的斜平面姿态参数、井斜角极值点参数完全相同；②无论井段终点位于图2中哪个区间，正反演模型都适用；③斜平面姿态和井斜角极值仅与井段始点的井斜角和工具面角有关，而与井段长度（即终点位置）无关；④极小和极大井斜角的值域分别为[0°，90°]和[90°，180°]，两个井斜角极值点的弯曲角相差180°；⑤斜平面下倾和上倾方向的倾斜角互为补角，空间圆弧轨迹的极小和极大井斜角也互为补角；⑥斜平面下倾和上倾方向的倾斜方位角相差180°，空间圆弧轨迹两个井斜角极值点处的方位角也相差180°；⑦相差180°的两个初始工具面角所钻出的两个空间圆弧轨迹位于同一个斜平面内，但这两个空间圆弧轨迹却是相背而行。

7 结论

可分别由正演模型和反演模型得到空间圆弧轨迹的井斜角方程和方位角方程，并计算出任一井深处的井斜角和方位角。空间圆弧轨迹所在斜平面姿态可用倾斜角和倾斜方位角来表征。通过空间圆弧轨迹的姿态能够唯一确定其所在斜平面的姿态。

空间圆弧轨迹或其趋势线存在井斜角极值点，极小和极大井斜角点的井眼轨迹切线分别指向所在斜平面的下倾和上倾方向。空间圆弧轨迹的极小和极大井斜角分别等于所在斜平面下倾和上倾方向的倾斜角，这两点处的井眼轨迹方位角分别等于所在斜平面下倾和上倾方向的倾斜方位角。

利用正演模型和反演模型求得的斜平面姿态参数、井斜角极值点参数完全相同，且斜平面姿态参数和井斜角极值点参数仅与井段始点的井斜角和工具面角有关，与井段长度无关。两个井斜角极值点的弯曲角和方位角均相差180°。

在始点井斜角相同的条件下，初始工具面角相差180°的两个空间圆弧轨迹具有相同的斜平面姿态。斜面倾角模式存在二义性，不宜作为空间圆弧轨迹的控制模式。推荐使用工具面角或定向方位角控制模式。

符号注释：

L——井深，m；ΔL——井段长度，m；α——井斜角，（°）；φ——方位角，（°）；κ——井眼曲率，（°）/m；R——曲率半径，m；ε——弯曲角，（°）；β——斜平面的倾斜角，（°）；β1——斜平面下倾方向的倾斜角，（°）；β2——斜平面上倾方向的倾斜角，（°）；ψ——斜平面的倾斜方位角，（°）；ψ1——斜平面下倾方向的倾斜方位角，（°）；ψ2——斜平面上倾方向的倾斜方位角，（°）；αext——井斜角极值，（°）；Lext——井斜角极值点的井深，m；εext——井斜角极值点的弯曲角，（°）；φext——井斜角极值点的方位角，（°）；αmax，αmin——井斜角极大值和极小值，（°）。下标：A，B，a，b，c，d——井段上不同位置点。

[1]API.API Bulletin D20 Directional drilling survey calculation methods and terminology[S].Washington D C:API,1985.

[2]国家能源局.SY/T 5435-2012 定向井轨道设计与轨迹计算[S].北京:石油工业出版社,2012.National Energy Administration.SY/T 5435-2012 Wellpath planning &trajectory calculation for directional wells[S].Beijing:Petroleum Industry Press,2012.

[3]Taylor H L,Mason C M.A systematic approach to well surveying calculations[J].SPE Journal,1972,12(6):474-488.

[4]Zaremba W A.Directional survey by the circular arc method[J].SPE Journal,1973,13(1):5-11.

[5]Blythe E J.Computing accurate directional surveys[J].World Oil,1975,181(2):25-28.

[6]McMillian W H.Planning the directional well:A calculation method[R].SPE 8337,1979．

[7]杨震,杨锦舟,韩来聚.随钻电磁波电阻率测井实时井眼影响校正[J].石油勘探与开发,2013,40(5):625-629.Yang Zhen,Yang Jinzhou,Han Laiju.A real-time borehole correction of electromagnetic wave resistivity logging while drilling[J].Petroleum Exploration and Development,2013,40(5):625-629.

[8]Brown D E.Programmed math keeps directional drilling on target[J].Oil &Gas Journal,1980,78(12):164-167.

[9]白家祉,苏义脑.定向钻井过程中的三维井身随钻修正设计与计算[J].石油钻采工艺,1991,13(6):1-4.Bai Jiazhi,Su Yinao.Design and calculation of 3D wellbore trajectories during directional drilling[J].Oil Drilling &Production Technology,1991,13(6):1-4.

[10]Liu Xiushan,Shi Zaihong.Improved method makes a soft landing of well path[J].Oil &Gas Journal,2001,99(43):47-51.

[11]刘修善,石在虹.给定井眼方向的修正轨道设计方法[J].石油学报,2002,23(2):72-76.Liu Xiushan,Shi Zaihong.A new method of path-correction planning with the desired direction[J].Acta Petrolei Sinica,2002,23(2):72-76.

[12]韩志勇.三维定向井轨道设计和轨迹控制的新技术[J].石油钻探技术,2003,31(5):1-3.Han Zhiyong.The new techniques of well trajectory design and well path control fit for 3D directional wells[J].Petroleum Drilling Techniques,2003,31(5):1-3.

[13]唐雪平,苏义脑,陈祖锡.三维井眼轨道设计模型及其精确解[J].石油学报,2003,24(4):1-4.Tang Xueping,Su Yinao,Chen Zuxi.Three dimensional well-path planning model and its exact solution[J].Acta Petrolei Sinica,2003,24(4):1-4.

[14]刘修善,郭钧.空间圆弧轨道的描述与计算[J].天然气工业,2000,20(5):44-47.Liu Xiushan,Guo Jun.Description and calculation of the well path with spatial arc model[J].Natural Gas Industry,2000,20(5):44-47.

[15]Sawaryn S J,Thorogood J L.A compendium of directional calculations based on the minimum curvature method[J].SPE Drilling &Completion,2005,20(1):24-36.

[16]鲁港,王刚,邢玉德,等.定向井钻井空间圆弧轨道计算的两个问题[J].石油地质与工程,2006,20(6):53-55.Lu Gang,Wang Gang,Xing Yude,et al.Two questions of space circular arc orbit calculation during drilling directional well[J].Petroleum Geology and Engineering,2006,20(6):53-55.

[17]刘修善,王超.空间圆弧轨迹的解析描述技术[J].石油学报,2014,35(1):134-140.Liu Xiushan,Wang Chao．Analytic description of spatial-arc wellbore trajectory[J].Acta Petrolei Sinica,2014,35(1):134-140.

[18]刘修善.井眼轨道几何学[M].北京:石油工业出版社,2006:287-289.Liu Xiushan.The geometry of wellbore trajectory[M].Beijing:Petroleum Industry Press,2006:287-289.

[19]韩志勇.定向钻井设计与计算[M].2版.东营:中国石油大学出版社,2007:304-308.Han Zhiyong.Design and calculation of directional drilling[M].2nd ed.Dongying:China University of Petroleum Press,2007:304-308.

[20]韩志勇.斜面圆弧形井眼的轨迹控制新模式[J].石油钻探技术,2004,32(2):1-3.Han Zhiyong.New control mode for well trajectory on circular arc with inclined planes[J].Petroleum Drilling Techniques,2004,32(2):1-3.

（编辑 胡苇玮 绘图 刘方方）

Evolution pattern and control mode of well deviation for circular-arc trajectories in space

Liu Xiushan1,Su Yi’nao2
(1.Sinopec Research Institute of Petroleum Engineering,Beijing 100101,China;2.CNPC Drilling Research Institute,Beijing 100083,China)

The well deviation equation of circular-arc trajectory in space was established,the solution methods to determine the posture of the inclined plane that the circular-arc trajectory lies on and the extreme value of inclination angle of the circular-arc trajectory were presented,and the evolution pattern and control mode of well deviation for circular-arc trajectories in space was revealed.Some parameters can be calculated by the forward model and inverse model respectively,including the inclination angle and azimuth angle at any point along a circular-arc trajectory,the inclined angle and inclined azimuth angle of the inclined plane that the circular-arc trajectory lies on and the various parameters at the point with extreme inclination angle,and the calculated results from the forward model are the same as those from the inverse model.There are two points with extreme inclination angles along a circular-arc trajectory or its trendline,and the tangent lines of wellbore trajectory at the points with minimum and maximum inclination angles point to downdip and updip directions of the inclined plane respectively,the bending angle and azimuth angle differences between the two points are both 180°.The posture of inclined plane and parameters at extreme inclination points relate to the inclination angle and tool face angle at the beginning point of well interval,but have nothing to do with the interval length.The inclined angle mode for controlling a circular-arc trajectory is ambiguous,so the tool-face angle or directional azimuth angle modes should be used.

drilling theory;directional drilling;wellbore trajectory;well deviation evolution

国家重点基础研究发展计划（973计划）“深井复杂地层安全高效钻井基础研究”（2010CB226700）；国家科技重大专项“海相碳酸盐岩油气井井筒关键技术”（2011ZX05005-006）

TE21

：A

1000-0747(2014)03-0354-05

10.11698/PED.2014.03.12

刘修善（1962-），男，黑龙江牡丹江人，博士，中国石化石油工程技术研究院教授级高级工程师，主要从事导向钻井工艺、井下信息测量与控制等方面的研究工作。地址：北京市朝阳区北辰东路8号北辰时代大厦9层，中国石化石油工程技术研究院，邮政编码：100101。E-mail：liuxs.sripe@sinopec.com

2014-02-20

2014-04-10