基于直线平行垂直关系美化三维线框模型
何 波, 高满屯, 王淑侠
(西北工业大学机电学院,陕西 西安 710072)
基于直线平行垂直关系美化三维线框模型
何 波, 高满屯, 王淑侠
(西北工业大学机电学院,陕西 西安 710072)
针对计算机线图解释中直线间几何关系可能存在不准确,从而出现视觉表达问题的不足,研究了基于直线平行垂直关系美化三维线框模型方法。首先,计算正视投影空间中三维线框模型中棱线方向矢量并选择基准棱线;然后,采用直线间平行垂直约束对线框模型中出现几何错误的直线进行校正,重新选择已校正棱线为基准棱线重复上述操作;最后根据新的棱线参数确定三维线框模型顶点新坐标。通过算例结果表明,该方法能够有效地解决线框模型中出现的平行垂直几何问题,达到线框模型视觉上的美化。
线图解释;线框图模型;几何结构;美化
在工程设计的概念设计阶段,设计者经常画出立体线图(草图),且需要反复对设计进行修改。目前,具有强大功能的CAD系统只能对设计的详细设计过程提供很大的帮助,而处理草
图的能力极弱,也不能直接将线图转换为三维物体结构信息,不便于在工程设计的概念设计阶段使用。
随着科学技术的发展,人机之间用图形进行通讯日益受到重视,在许多场合显示出其重要性。为使计算机能“看”懂物体投影线图,需要研究计算机解释投影线图的机理。计算机分析、处理和理解线图的研究成果可用于互联网、CAD系统中的人机通讯接口、逆向工程及计算机视觉系统等领域,能缩短图形输入时间,减轻人-机通讯中“人”的工作量。
线图解释[1]是计算机视觉和模式识别的一个重要研究领域。线图的解释就是根据物体(或场景)的一幅或多幅投影图像理解三维空间中的景物。对于高度进化的人类视觉而言,理解三维景物是一件比较容易的事情,但要用计算机来模拟这一过程,是一项极其困难的工作。
经过计算机解释立体线图后,从二维线图恢复的三维物体线框图模型,即使拓扑结构完全正确,恢复出的三维物体线框模型仍然可能存在几何结构缺陷(如图 1所示),而线框模型是构造三维物体实体模型的基础。只有在保证三维物体线框模型拓扑和几何结构正确的情况下才能得到正确的三维物体实体模型。
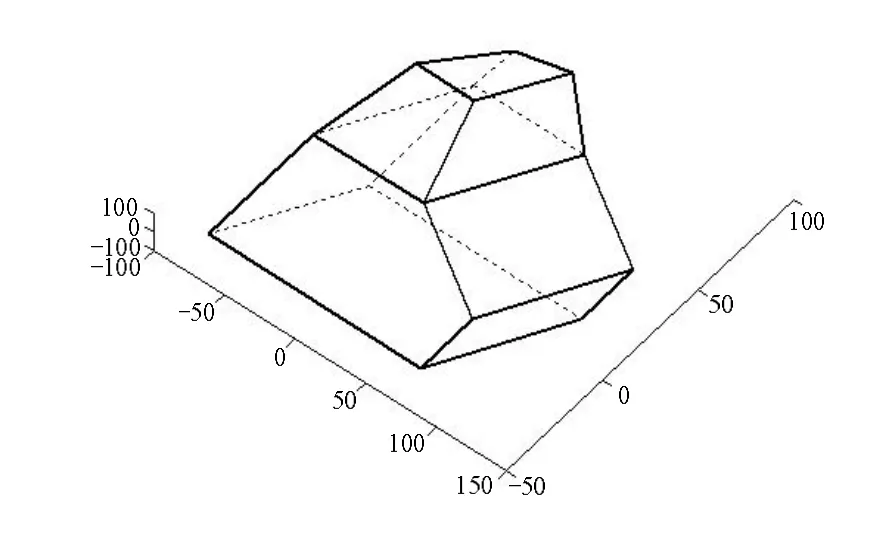
图1 恢复的三维线框模型
从二维线图恢复的三维线框模型经常出现如下一些问题[2-4]:①三维物体中应该平行的平面或直线未平行;②三维物体中应该垂直的平面或者直线不垂直;③三维物体上共平面的点实际上不共面;④三维物体的几何结构中对称的部分不完全对称;⑤三维物体的几何结构不符合力学性能、材料性能的要求,如壁厚不均匀,即面的距离不合适等;⑥三维物体中孔的位置不正确;⑦三维物体中两个表面之间的夹角不符合要求。
Lipson和Shpitalni[5]提出了一个从单幅、不准确的二维线框草图恢复三维物体结构的优化算法,线图中的不准确包括顶点位置误差和线图不完整。但不足之处是初始值不宜选取,而且图像中各种规则的提取比较困难。Company等[6]利用模拟退火技术进行优化,得到了局部最优解,优化结果能得到最可能符合人类视觉心理线图。但是得到的最优解有可能是局部最优解而不是全局最优解。储珺等[7]采用优化和迭代技术对线图进行校正,使校正后的线图是一个平面立体的正确投影,恢复的平面立体与原画线图表示的平面立体尽量接近,但这并不是一个合适的做法,实际上解释线图获得三维物体是最终目标,而非三维物体的重投影尽量与原线图一致。莫白声[8]依据线图空间结构中IE关系及FV关系采用了迭代方法对线图进行了修正。但是其不足之处在于迭代运算中存在矩阵的降阶问题,而且其所用方法最适用于对局部存在的误差进行处理。Lee和Fang[9]研究了一种使用图形上提取的立方体角信息及所标识面信息作为初始信息的线图恢复方法,这种方法非常精确而且效率很高,但同时该方法对初始值的精确要求很高,如果采用了不准确的初始信息,则恢复的三维模型会出现扭曲变形,达不到线图解释基本目的。
现有线图解释优化方法虽然能从线图中恢复平面立体三维结构,但仍会出现恢复的平面立体有时不符合人类视觉感受,不具备美化效果。若线图解释中考虑几何元素之间的相对位置关系和度量关系,则线性系统将转化为非线性系统,使问题变得更复杂。所以本文提出新的观点,将计算机线图解释分为两步,首先进行传统意义上的三维恢复,然后采用本文提出的美化方法对线框图进行后期处理,得到人类视觉感官上可以接受的三维线框模型。
1 基于直线关系美化三维物体
1.1 三维物体线框模型美化算法
本文主要基于棱线之间的平行、垂直、相交关系美化三维物体的线框模型。基于直线平行、垂直关系的三维线框模型美化算法流程图如图2所示。
1.2 棱线之间的平行性约束判断及修正
从二维线图到三维物体线框模型中的过程中,二维线图上平行的直线,在三维物体线框模型中理论上应该是平行或异面,而实际模型中,棱线都是一些线段,而三维物体上的线段数量又
在可计算的范围之内,因此异面直线的问题在实际应用上可以不用考虑。三维物体线框模型中棱线之间的平行性约束,由于误差、误差传播以及二维线图中的误差等原因,可能没有满足或者没有精确满足,因此,三维物体线框图中的棱线平行性约束有些需要修正。

图2 算法流程图
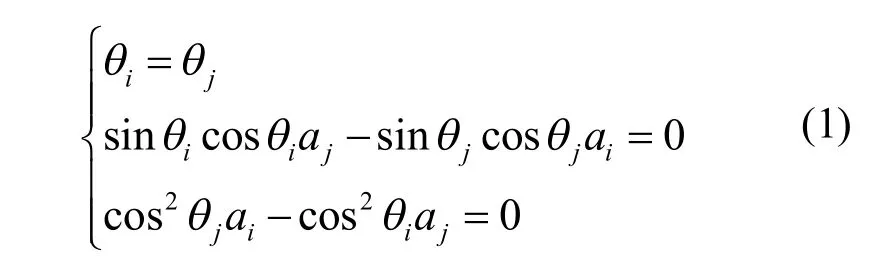
式(1)中各个参数均为正轴测投影下三维直线法线式表达式[1]中的参数,其中ρ为空间直线的投影直线的法线长,θ表示为投影直线夹角,aj与 dj为空间直线推导中的参数。
根据式(1),棱线平行所满足的约束条件为:

为简化形式,令:

根据三维物体线框模型的数据进行判断,验证线框模型中应该平行的棱线是否平行,然后根据平行性约束,对不满足平行性的棱线进行修正。如图3所示,该线框模型中一共有12个顶点,18条棱线(其中有平行棱线15对)。先获得的18条棱线的参数和12个顶点的z坐标值。

图3 恢复的三维物体线框模型
1.3 棱线之间的垂直性约束判断及修正
由于误差、误差传播以及二维线图中的误差等原因,三维物体线框模型中棱线之间的垂直性约束可能没有满足或者没有精确满足。因此,三维物体线框图中的棱线垂直性约束有些需要修正。

如图3所示,以三面顶点1为例来分析,属于顶点1的三条棱线中,若与不垂直,以棱线为基准棱线,因此需要调整 L(1,11)的方向矢量。具体方法如下:
(1)设L(1,11)的方向矢量为 (sin2α ,-cosαsinα, - a),其中a和α为需要重新确定的未知参数;
(3)求解方程组得便可得 a和α的数值,即为L(1,11)所需调整数值;其他棱线之间垂直性的判别和修正类似。
1.4 棱线相交性判断与修正
三维物体线框模型中的棱线经过利用垂直性和平行性约束进行调整其方向矢量后,有可能就不满足棱线的相交性约束了,因此,经过调整以后的三维物体线框模型需要进一步判断和修正三维物体线框模型上应该相交棱线是否仍然相交。经过上面两步调整之后,各条棱线的方向矢量已经确定,棱线是否相交只与棱线参数d有关。因此,如果棱线不满足相交的约束,只需调整棱线的参数d。空间两条棱线相交的约束条件为:
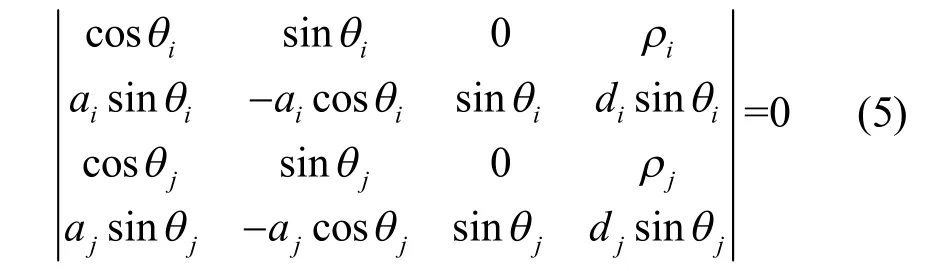
其中 ai和 aj为已知,如果两条棱线不相交,则固定基准棱线不动,调整另外一条棱线的参数d。
调整过棱线的方向矢量之后,棱线对之间满足了平行性与垂直性约束,但各棱线对之间可能不再满足相交的约束条件。因此,需要在不改变棱线方向矢量的条件下调整棱线的空间位置。由空间直线的方程:

式中,ρ、sinθ、cosθ为从二维线图中所获得的已知信息。又由于空间棱线的方向矢量
为已经得以确定,参数 a已经完全确定。因此,调整三维物体上棱线的位置只能调整参数d。
具体调整方法:任选一条棱线为基准棱线,如选择棱线L(1,2)为基准,即L(1,2)的参数不变,根据棱线 L(1,2)与棱线 L(1,4)的相交约束,即根据式(5),获得 d1的值。同理,获得与棱线 L(1,2)相交的所有棱线的d值;再选已经确定d值的棱线为基准棱线,根据棱线对之间的相交约束获得与其相交所有棱线的d值;依次调整三维物体上的其他所有棱线的位置。
1.5 三维物体上顶点坐标的重新确定
对一个三维物体线框模型经过上述各个过程的一系列调整之后,三维物体线框模型上各个顶点的位置也随之发生了改变。因此,需要重新确定三维物体线框模型的所有顶点的位置。
三维物体上棱线的参数确定以后,确定三维物体上顶点的新位置就很容易了。根据三维物体最初始的顶点与棱线的拓扑关系,利用空间两条直线相交求交点的方法可获取顶点的新坐标。
2 算例演示
算例1图4是从线图解释恢复的三维物体线框模型。根据人类视觉习惯和工程实际要求,该三维物体线框模型中的棱线有些应该满足垂直性和平行性约束条件,但恢复出的三维物体线框模型没有满足这些条件,如L(1,2), L(1,3), L(1,4)显然与对应棱线不平行而且相互之间也未垂直。因此需要对恢复的三维物体线框模型进行美化。采用本文方法美化后的三维物体线框模型,如图5所示。从图中可以看出,采用本文美化方法达到线框模型视觉上的美化。

图4 原三维物体线框模型

图5 美化之后的三维物体线框模型
算例2图6是从线图解释恢复的三维物体线框模型。由于线图中一个节点的位置不正确,导致恢复的三维物体线框模型中一些棱线不满足垂直性和平行性约束条件。采用本文方法美化后的三维物体线框模型如图7所示。从图中可以看出,采用本文美化方法达到线框模型视觉上的美化。

图6 原三维线框模型

图7 美化之后的三维物体线框模型
3 结 论
提出了基于直线平行约束、垂直约束、相交关系美化三维物体线框模型的算法。通过大量美化三维物体的实践,作者认为,在美化三维物体时,利用的关系顺序最佳为:平行→垂直→平行→…→平行→垂直→相交。采用本文美化方法美化有误差的三维物体线框模型,获得了符合实验目标的三维物体线框模型,达到线框模型视觉上的美化。
[1] 高满屯, 储 珺, 董黎君. 计算机解释立体线图的方法与实践(2009)[M]. 西安: 西北工业大学出版社, 2009: 171-184.
[2] Varley P A C, Martin R R, Suzuki H. Can machines interpret line drawings?[C]//Sketch-Based Znterfaces and Modeling 2004: Eurographics Symposium Procedings. Aive-la-Ville, Switzerland: Eurographics, Association, 2004: 107-116.
[3] 高满屯, 储 珺, 董黎君. 线图解释研究综述[J].工程图学学报, 2006, 27(5): 1-11.
[4] 储 珺. 从单幅画隐线立体线图恢复平面立体三维结构的研究[D]. 西安: 西北工业大学, 2005.
[5] Lipson H, Shpitalni M. A new interface for conceptual design based on object reconstruction from a single freehand sketch [J]. CIRP Annals-Manufacturing Technology, 1995, 44(1):133-136.
[6] Company P, Contero M, Conesa J, Vicent A P. An optimisation-based reconstruction engine for 3D modelling by sketching [J]. Computer Aided Design, 2004, 28(6): 955-979.
[7] 储 珺, 高满屯, 陈国定. 基于迭代技术的有误差单幅线图的计算机解释[J]. 模式识别与人工智能, 2005, 18(5): 615-620.
[8] 莫白声. 平面立体线图解释的误差分析和误差修正研究[D]. 南昌: 南昌航空大学, 2007.
[9] Lee Y T, Fang Fen. 3D reconstruction of polyhedral objects from single parallel projections using cubic corner [J]. Computer Aided Design, 2011, 43(8):1025-1034.
Beautification of Wireframe Model of Three-Dimensional Objects Based on Parallel and Vertical Linear Relationship
He Bo, Gao Mantun, Wang Shuxia
(College of Electromechanical, Northwestern Polytechnical University, Xi′an Shaanxi 710072, China)
In order to solve the problem that errors may exist in the geometrical interpretation of the relationship between the lines and thus result in the inadequacy in visual expression,a method is developed on parallel and vertical linear relationship for beautifying the wireframe model of three-dimensional objects. Firstly, the ridge direction vector of the three-dimensional wireframe models in the face projection space is calculated and a benchmark ridge is chosen; then geometric errors appearing in wireframe model are corrected by the parallel and vertical constraint of the linear relationship, the corrected ridge is reselected as the new benchmark and a repeatition of the operation is conducted. Finally, the new coordinates of the vertices of the three-dimensional wireframe models are calculated according to the new ridge parameter. The numerical example shows that the proposed methods can effectively solve the parallel and vertical geometric problems in the wireframe model to beautify the wireframe model.
line drawing interpretation; wireframe model; geometry structure; beautification
TP 391.41
A
2095-302X (2014)03-0325-05
2013-11-08;定稿日期:2014-01-23
国家自然科学基金资助项目(51105310;513101435)
何 波(1986-),男,陕西宝鸡人,硕士。主要研究方向为计算机图形学。E-mail:heyu1743@163.com
高满屯(1962-),男,山西襄汾人,教授,硕士。主要研究方向为投影理论、图形学、计算机视觉、几何学。E-mail:gaomant@nwpu.edu.cn

