高精度UT1-UTC差分预报方法研究

陈略,唐歌实,胡松杰,平劲松,许雪晴,夏金超

(1.北京航天飞行控制中心航天飞行动力学技术重点实验室;北京100094; 2.中国科学院国家天文台;北京100012;3.中国科学院上海天文台;上海200030)

高精度UT1-UTC差分预报方法研究

陈略1,唐歌实1,胡松杰1,平劲松2,许雪晴3,夏金超1

(1.北京航天飞行控制中心航天飞行动力学技术重点实验室;北京100094; 2.中国科学院国家天文台;北京100012;3.中国科学院上海天文台;上海200030)

针对卫星导航所需的高精度地球定向参数(EOP)中的UT1-UTC预报问题,提出了基于双差分LS+ AR的UT1-UTC参数预报方法。对UT1-UTC观测数据进行跳秒检测、固体地球带谐潮汐项改正,然后对改正后的UT1-UTC数据进行双差分处理,增强数据平稳性;采用最小二乘拟合(LS)与自回归(AR)分析方法对差分处理后的数据进行分析与预报;对预报结果进行逆差分处理与潮汐项改正外推、跳秒恢复,获取高精度的UT1-UTC预报值。通过与国际EOP_PCC预报结果对比表明,UT1-UTC短期预报精度与EOP_PCC较优的预报精度相当,其中1天UT1-UTC预报精度优于0.03 ms,优于EOP_PCC预报结果。介绍了北京航天飞行控制中心的UT1-UTC每日例行预报情况。

地球定向参数;UT1-UTC预报;差分处理;AR模型;潮汐项改正

0 引 言

高精度地球定向参数(Earth orientation parameters,EOP)是地球参考架与天球参考架实时转换时的基础参数[1]。VLBI、GNSS、DORIS、LLR、SLR等现代空间大地测量技术可精确地测量地球定向参数[2-3]。高精度EOP在载人航天、深空探测等任务中具有重要价值,尤其是在航天器实时、高精度导航方面不可或缺。目前,由于EOP解算结果在时间上有滞后,因此EOP参数高精度预报对于航天器导航显得十分重要,且EOP预报对于与EOP相关的地球物理动力学理论分析具有重要价值。

EOP预报中的极移预报、UT1-UTC预报是EOP预报中的热点研究内容。目前,有多种预报方法应用于EOP的预报中,如最小二乘(LS)外推法[4]、最小二乘联合自回归分析法(LS+AR)[5]、神经网络预报法[6]、谱分析最小二乘外推法[7]、小波分解与自回归分析方法[8]等。国际地球自转与参考系服务(IERS)组织于2005年10月发起了首次全球地球定向参数预报比赛活动(EOP_PCC),旨在号召全世界EOP预报人员运用不同方法来预报EOP,用以分析现有方法的特点及使用情况。LS+AR预报方法是预报精度最高的方法之一。但运用LS+ AR预报方法时,LS模型参数的选择,AR模型阶数的确定,非平稳序列AR分析,EOP预报精度评估等是进行EOP预报的关键问题。现有LS+AR预报方法在对数据平稳性要求方面的研究较为欠缺,在一定程度上限制了EOP预报精度。

本文从分析数据的平稳特性出发,提出了双差分LS+AR预报方法,用于实现对EOP中UT1-UTC高精度预报,并获取了高精度的UT1-UTC短期预报结果。与此同时,同时介绍了与EOP_PCC进行精度比较的结果,此外,介绍了北京航天飞行控制中心EOP参数高精度预报软件每日例行情况。

1 预报理论与方法

1.1 最小二乘(LS)模型

对UT1-UTC观测数据进行最小二乘模型拟合时,模型包括线性项与周期项(周年项、半年项、9.3年项、18.6年项等),其最小二乘模型如式(1)所示。

式中:t为序列的UTC时间,单位为年;A,B,C,D1, D2,E1,E2,…为模型的拟合参数;p1,p2,…为拟合周期,可根据实际情况确定模型形状。

1.2 AR模型

1.2.1 AR模型定义

AR模型表示平稳随机序列xt(t=1,2,…,N)与t时刻以前的规律性变化和t时刻白噪声的关系,其数学模型如式(2)所示

式中:φ1,φ2,…,φp为模型参数;a为白噪声;p为模型阶数,称上式为p阶自回归模型,简记为AR(p);为白噪声的方差。

1.2.2 AR模型阶数确定

运用AR模型关键在于确定模型阶数p,可采用最终预报误差(final prediction error criterion, FPE)准则、AIC(akake information criterion)准则、BIC准则、矩阵奇异值分解(singular value decomposition,SVD)准则来确定模型的阶数。

本文采用解Yule-Walker方程方法来估计模型阶数,其基本原理[9]如下:

根据自协方差函数的定义,一个平稳、正态、零均值的随机过程{xt}的自协方差定义为

其中,E表示集合平均算子,即数学期望,{xt}的零均值性导致其自协方差函数与自相关函数是一致的,而且作为Rk的特例,当k=0时,得{xt}的方差函数

自相关系数定义为

显然,ρ0=1。由许瓦兹不定式,知,的取值范围为

对于平稳时间序列,当ρk=0时,表示序列前后无关,即为白噪声;当时,表示序列前后取值的关系不但完全确定,而且前后取值相等,即序列为常值序列。

对式(2)中左右两边乘以xt-k,再取数学期望并除以R0,得到

分别令k=1,2,…,p,并注意自协方差函数是偶函数的性质,R-k=Rk,因而ρ-k=ρk,可得线性方程组如下

分别令k=1,2,…,n,则可得方程的个数等于未知数φ1,φ2,…,φn的个数,即上式等效为式(9)。

此式成为Yule-Walker方程,其中ρ为n×1的列矩阵,T为n阶仿阵,称为Toeplitz矩阵,如式(10)所示。

T中各元素可按定义估计出。由于T是满秩的,因此可容易求出模型参数如式(11)所示。

本文采用FPE准则来确定AR模型阶数。FPE准则函数如式(12)所示。

1.3 精度评估

为了评估预报精度,采用EOP预报中的通用精度评估准则-平均绝对误差(mean absulute eroor, MAE)作为预报结果的精度指标,其计算公式如下:

式中:o为实际观测值;p为预报值;i为预报跨度;n为预报期数。

2 双差分LS+AR预报流程

双差分LS+AR的UT1-UTC预报方法的实现流程如图1所示。

图1 双差分LS+AR UT1-UTC预报流程图Fig.1 UT1-UTC prediction process of differential LS+AR method

3 计算分析

利用IERS公布的EOP数据进行预报与精度验证。选取EOP 05C04的极移数据进行分析,便于与EOP_PCC结果进行比较。时间跨度为1989年1月1日～2009年12月31日,数据采样频率为1点/天。预报的基础时间序列为1989年1月1日～2009年10月2日,对2009年10月3日至2009年12月31日的EOP极移进行预报,并将预报值与真实观测值进行比较,评估预报精度。预报跨度分别从1～30天,预报期数为90期。具体预报结果如下所述。

图2为1989年—2009年的UT1-UTC的时间变化图,其中图2(a)为原始的UT1-UTC波形图;图2(b)为剔除跳秒后的UT1-UTC图;图2(c)为固体地球带谐潮汐项改正图,依据IERS2010规范进行改正;图2(d)是经过跳秒剔除与潮汐项改正后的UT1-UTC时间序列。

图3为1989年—2009年UT1-UTC双差分后的LS拟合结果。从图中可以看出,经过双差分后的UT1-UTC序列具有明显的平稳性。利用LS所得参数进行外推,利用AR模型对LS拟合后的残差进行预报,将LS外推值与AR模型外推值进行相加,即得跨度为1天的预报值。其中,在进行AR预报过程中,AR模型阶数的确定是AR预报最关键步骤,本文采用FPE准则确定模型阶数,在阶数确定过程中采用迭代搜索方法确定最优模型阶数,阶数搜索范围为1～100,采用FPE准则计算出每一项FPE值,其中最小FPE值对应阶数即为最优的AR模型阶数。

按照图1的处理流程,对预报初值进行逆双差分处理、固体地球带谐潮汐项改正外推、跳秒恢复后,即可获得第一天的UT1-UTC预报值。在得到第1天的预报值之后,将第1天的预报值加入到基础序列中,重新按照图1的处理流程进行第2天的UT1-UTC预报。以此类推,可获取不同预报跨度的UT1-UTC预报结果。

图2 1989-2009年UT1-UTC的时间序列分布图Fig.2 Time sequence of UT1-UTC from 1989 to 2009

图3 1989-2009年UT1-UTC双差分LS拟合结果Fig.3 Differential LS fitting results of UT1-UTC from 1989 to 2009

基于以上方法进行90期预报,并利用平均绝对误差(MAE)准则评估UT1-UTC预报精度,其结果如图4所示,具体数值如表1所示。

图4 BACC的UT1-UTC短期预报结果Fig.4 Short term prediction results of UT1-UTC in Beijing Aerospace Control Center

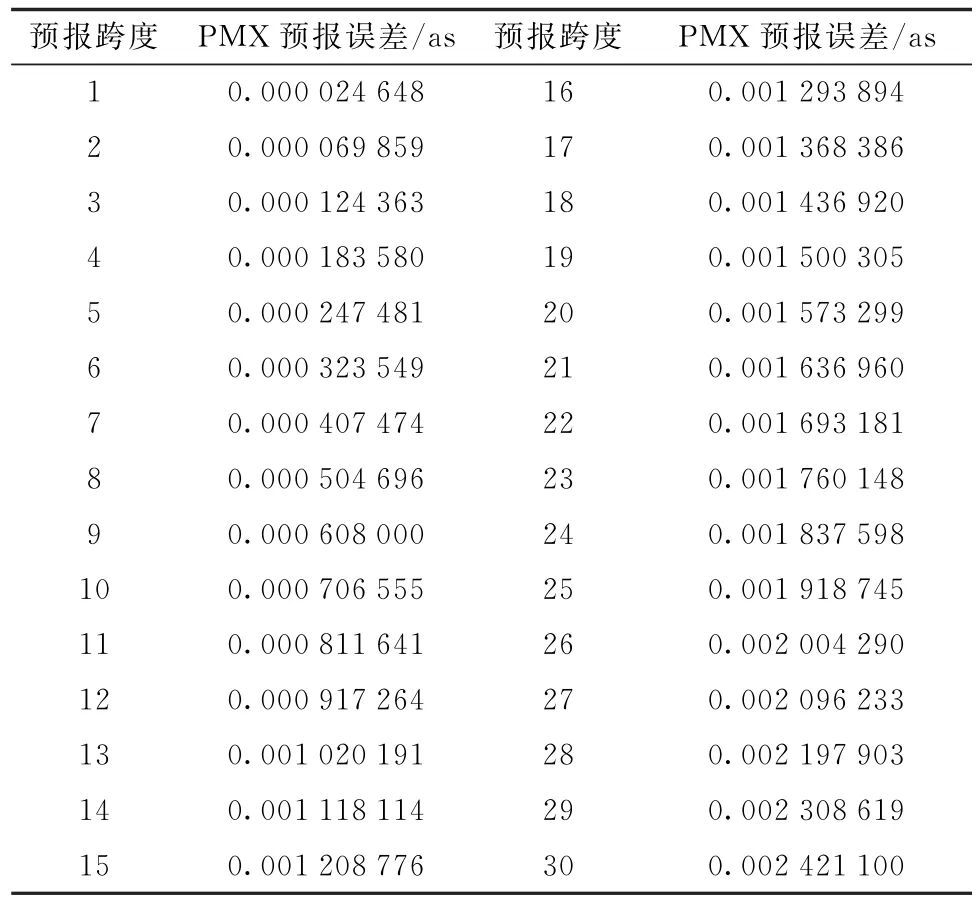
表1 BACC的UT1-UTC短期预报MAE结果Table 1 MAE of UT1-UTC short term prediction in Beijing Aerospace Control Center

全球性的EOP预报比对运动(earth orientation parameters prediction comparison campaign,EOP_PCC),共有8个国家12名时间序列分析领域的顶尖级专家学者参与,涉及20余中预报方法。EOP_PCC运动分为10天超短期预报, 30天短期预报,500天长期预报。

本文将预报结果与EOP_PCC的结果进行比对分析,分析进行超短期预报比对,与短期预报比对。图5为EOP_PCC的预报结果,图6为本文的预报结果。

从结果可以看出,本文的UT1-UTC短期预报精度与EOP_PCC的预报精度相当。对于1天预报精度,本文UT1-UTC预报精度优于EOP_PCC预报精度。本文获取的1天UT1-UTC预报精度优于0.03 ms。EOP_PCC的UT1-UTC一天预报误差[1]在0.08 ms水平。

图5 EOP_PCC的UT1-UTC短期预报结果Fig.5 Short term prediction results of UT1-UTC in EOP_PCC

图6 BACC的UT1-UTC短期预报结果Fig.6 Short term prediction results of UT1-UTC in Beijing Aerospace Control Center

4 UT1-UTC每日例行预报

北京航天飞行控制中心(BACC)飞行动力学重点实验室开发了EOP高精度预报软件,可实现对UT1-UTC每日例行预报与发布。该软件每日从互联网上自动化下载UT1-UTC解算数据,而后进行UT1-UTC预报并生成预报结果,同时输出BACC/ IERS/美国海军天文台(USNO)的UT1-UTC预报的比较结果,用以每日评估BACC的UT1-UTC预报。BACC的EOP预报软件输入的UT1-UTC解算数据由两个部分组成:IERS网站公布的EOP 08 C04序列+USNO最近一个月的解算序列。

图7 2014-11-03 UT1-UTC 30天预报结果比较Fig.7 UT1-UTC 30 days prediction comparing results on 2014-11-03

图8 2014-11-04 UT1-UTC 30天预报结果比较Fig.8 UT1-UTC 30 days prediction comparing results on 2014-11-04

图9 2014-11-05 UT1-UTC 30天预报结果比较Fig.9 UT1-UTC 30 days prediction comparing results on 2014-11-05

图7～图9显示了2014年11月3—5日, BACC的UT1-UTC预报结果与IERS/USNO结果对比图。在图7～图9中,圆圈表示BACC的预报结果,正方形表示USNO的预报结果,梅花形表示IERS的预报结果。从以上图中可以看出,BACC的UT1-UTC预报结果趋势与IERS、USNO基本一致,且BACC 30天的UT1-UTC预报结果基本位于IERS与USNO之间,这说明了北京中心UT1-UTC预报结果有效性。

5 结束语

本文提出了基于双差分LS+AR的UT1-UTC预报方法,详细介绍了理论方法与处理流程,并介绍了BACC的UT1-UTC每日例行预报情况。通过对IERS实际的EOP中UT1-UTC进行预报与比对分析,本文的UT1-UTC预报精度与EOP_PCC较优的短期预报精度相当。本文获取的1天UT1-UTC预报精度优于0.03 ms,优于EOP_PCC每日预报结果。

相比于传统LS+AR的地球定向参数预报方法,本文重点从AR模型输入数据的平稳性要求方面进行考虑,采用了双差分预处理方法,用以提高UT1-UTC数据的平稳性,使其更加适应利用AR模型进行预报。此外,AR模型阶数确定采用了迭代搜索方式选择最优模型阶数。通过以上两项步骤,可有效提高对UT1-UTC的高精度预报。

后续将进一步研究本文提出的双差分LS+AR预报方法在极移、LOD预报上的应用,同时将进一步评估该方法在对EOP参数长期预报中的精度与适用性。

[1]Kalarus M,Schuh H,Kosek W,et al.Achievements of the Earth orientation parameters prediction comparison campaign [J].Journal of Geodynamics,2010(62):587-596.

[2]Tobias Nilsson,Robert Heinkelmann,Maria Karbon,et al. Earth orientation parameters estimated from VLBI during the CONT11 campaign[J].Journal of Geodesy,2014(88): 491-502.

[3]许雪晴,周永宏.地球定向参数高精度预报方法研究[J].飞行器测控学报,2010,29(2):70-76.[Xu X Q,Zhou Y H. High precision prediction method of Earth orientation parameters[J].Journal of Spacecraft TT&C Technology, 2010,29(2):70-76.]

[4]Xu X,Zhou Y,Liao X.Short-term earth orientation parameters predictions by combination of the least-squares, AR model and Kalman filter[J].Journal of Geodynamics, 2010(62):83-86.

[5]Guo J Y,Li Y B,Dai C L,et al.A technique to improve the accuracy of Earth orientation prediction algorithms based on least squares extrapolation[J].Journal of Geodynamics, 2013(70):36-48.

[6]Wang Q J,Liao D C,Zhou Y H.Real-time rapid prediction of variations of Earth's rotational rate[J].Chin.Sci.Bull, 2008(53):969-973.

[7]Akulenko L D,Kumakshev S A,Rykhlova L V.A model for the polar motion of the deformable Earth adequate for astrometric data[J].Astron.Rep.,2002(46):74-82.

[8]Kosek W,Kalarus M,Johnson T J,et al.A comparison of LOD and UT1-UTC forecasts by different combination prediction techniques[J].Artif.Satell,2005(40):119-125.

[9]杨叔子.时间序列分析的工程应用[M].武汉:华中科技大学出版社,2007:184-189.[Yang S Z.Time series analysis in engineering application[M].Wuhan:Huazhong University of Science&Technology Press,2007:184-189.]

通信地址:北京海淀区5130信箱120号(100094)

电话:(010)66362814

E-mail:luechen0912@163.com

[责任编辑:宋宏]

High Accuracy Differential Prediction of UT1-UTC

CHEN Lue1,TANG Geshi1,HU Songjie1,PING Jinsong2,XU Xueqing3,XIA Jinchao1
(1.National Key Laboratory of Science and Technology on Aerospace Flight Dynamic,Beijing Aerospace Control Center, 100094 Beijing,China;2.National Astronomical Observatory,Chinese Academy of Sciences,100012 Beijing,China; 3.Shanghai Astronomical Observatory,Chinese Academy of Sciences,200030 Shanghai,China)

This paper proposes a prediction method of UT1-UTC in Earth orientation parameters(EOP)by dual differential least-squares(LS)and autoregressive(AR)model.Firstly,leap seconds are removed in UT1-UTC observations,and Earth zonal harmonic tidal are corrected.Then,the corrected UT1-UTC are processed by dual differential method,the stationarity of polar motion parameters is improved.LS+AR method is utilized to analyze the dual differential UT1-UTC to obtain the preliminary prediction results.Finally,the preliminary prediction results are processed by inverse dual differential method,and tidal correction are extrapolated and leap seconds are recovered to obtain high accuracy UT1-UTC prediction results.The prediction results are compared with EOP prediction comparison campaign(EOP_PCC)results.It shows that the short-term UT1-UTC parameters prediction error is at the same level of EOP_PCC.The one day prediction accuracy of UT1-UTC is less than 0.03ms,which is better than EOP_PCC one day UT1-UTC prediction accuracy.And,the daily routine UT1-UTC prediction in Beijing Aerospace Control Center is introduced.

Earth orientation parameters;UT1-UTC prediction;dual differential;AR model;earth zonal harmonic tidal correction

P228

:A

:2095-7777(2014)03-0230-06

10.15982/j.issn.2095-7777.2014.03.012

陈略(1983—),男,工程师,主要研究方向:地球自转参数高精度解算与预报,无线电测量与科学应用。

2014-07-28

2014-08-19

国家自然科学基金(41304026);国家重点基础研究发展计划(973计划)项目(2015CB857101)