用逐步图解法对堰闸流量计算公式系数的再分析

□王继民（漯河水文水资源勘测局）

1 用逐步图解法探索堰闸流量计算公式

1.1 问题所在

在计算堰闸过水流量或流量系数时，按照水力学公式，堰闸上、下游两组水尺相距很近时，水流的沿程抗阻可不予考虑，只有局部抗阻导致的水头损失。但在实际运用中堰闸上下游两组水尺间距较远，以其水位差算得的流量系数成果与水力学所说的流量系数的含义有所出入，其中包括一部分河床糙率系数在内，如不考虑，分析成果就不够理想。

1.2 成因分析

鉴于堰闸站的测量成果中，有的自变量对因变量的影响，不是一个幂数或系数所能概括的，而需要分段定线，得出几个幂数或系数，获得几个公式，才不影响精度，因此不宜采用一般的回归分析。如果用普通坐标纸点绘多变量相关的等值线，会受到资料限制，有的等值线仅有一、二个点据太少，可靠性差，且又不便求出相关公式对它们的内在联系进行说明。因此，需要改换思路和方法，对其进行分析和处理。

1.3 思路与方法

如果以水力学公式为基础，从统计学观点出发，并遵照逐步回归分析方法的思路，用逐步图解法直接对堰闸流量计算公式进行分析,这样，既能逐步消除各个自变量对因变量的影响，又可在图上明显标出突出点据，便于分析研究和处理。

所谓逐步图解分析，就是根据水力学出流公式，先选取与因变量有关的一个自变量点绘相关图，消除它对因变量的影响后，再点绘第二自变量与因变量的相关，并消除它（第二自变量）对因变量的影响。然后，据以验证第一自变量与因变量的相关，如此经过反复验证，直至相关得出的计算公式能满足所需精度要求。如闸上下游水位差较大，且其系统误差很小不予考虑时，水位差的幂数采用1/2，便可一次分析成功。

2 实例分析验证

为了验证逐步图解法在堰闸站流量整编中的实用性，现结合几种常见的堰闸出流流态的实例。

2.1 沉溺式孔流

由于堰闸的形式有多种，影响堰闸沉溺式孔流的因素也较多，其变化规律亦较复杂。以平底闸为例，其沉溺式孔流的流量计算，按照水力学公式为：

式中：Q—流量（m3/s），M—流量系数，b—闸门开启宽度（m），E—闸门开启高度（m），Z—闸上下游水位差（m）。

从上式中可以看出，影响流量的几个因子，其幂数是不变的，但由于以上所分析的原因，不能适合每一个堰闸的具体情况，并且系数M值是一个变量因子而并非常数，这给流量计算带来许多不便。因此（1）式可改写为

式中：Mc—流量系数（可以消除其他影响因素），α、β—统计参数。

按照（2）式分析Mc、α、β3个参数，假设α为1（如流量测验点据较多，也可在双对数值上点绘e~Q相关图,找出某一固定Z值下的e~Q相关线的斜率，即为e的初试幂数α值）。

根据上式将Q/e及Z值对应，点绘在双对数值上，初步消除e的影响，便可由图解法求得第一次的Mc及β值。

图1为江都闸沉溺式孔流1982年及2000年实测成果相关图。从其相关线上量取一段横坐标△x（最好取5~10 cm）及相应的Δy，则Δy/△x即为所求的β值。本例所求得的β=0.52，那么（2）式可写为：

图1 沉溺式孔流图Q/e～Z相关图B=60 m

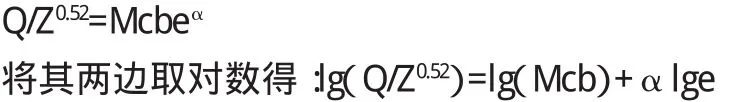
再将Q/Z0.52及e值对应，点绘在双对数纸上，见图2。

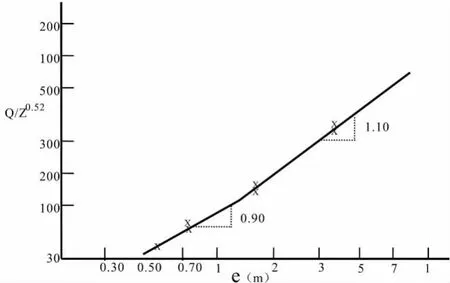
图1 沉溺式孔流图Q/e～Z相关图B=60 m

根据图2用图解法求得：当e≤1.50m时，α=0.92，Mcb=200，

需要说明的是，在图上查读Mc时，如横坐标为1的点在图幅之外，可在相关线上选取二三个点，读的e值及相应的Q/Z0.52值，用求得的α值等代入流量计算公式，推算出几个Mc值，然后取其均值。通过对24次测验点据，按照（3）及（4）式所推算出的流量Q推，与实测流量Q测进行比较，它们的相对误差δ均<±5%合格率100%，精度符合规范要求，可不再进行反复校正。

2.2 自由式孔流

2.2.1 实用堰自由式孔流

用（7）和（8）式验算石良河泄洪闸自由式孔流19次测验成果，计算其相对误差δ均<±5%，精度符合规范要求。

2.2.2 平底闸自由式孔流

通过对横山等水库泄洪闸自由式孔流资料的流量计算公式的分析，其相对误差及精度均在规范要求范围之内。惟其统计参数α值在0.78~0.90，β值在0.73~0.75之间，与实用堰自由式孔流出流公式有所不同，但分析方法与其相同。

2.3 沉溺式堰流

经过对29次实测资料的验算，有26次相对误差δ＜±5%；两次小水位差的相对误差δ介于±5～10%之间，合格率为96.60%，符合规范要求。从图解分析得出的流量计算公式中h的幂数为1.47，较水力学公式大0.47，这是由于一般堰闸上下游断面之间距离较远，其沿程抗阻对流量的影响，往往大于闸孔的局部抗阻的影响。因此它和明渠水流类似，堰上水深h不但标示了过水断面的大小，对河道流速也有一定的影响。

按照上式对实测成果进行验算，合格率与之前方法相近，说明二者均可以使用，而后者对于同类型堰闸的参数综合比较方便。

3 综合评定

通过以上综述分析，采用逐步图解法，对堰闸站几种常见的出流流态均可适用，分析其流量计算公式和流量系数，不但方便分类综合，又可以提高整编成果精度，更有利于在站分析整编的四随工作，对流量测验具有一定的指导意义。