岸基防空兵对高强度攻击目标火力运用*

严建钢，杨士锋，杨大伟

（海军航空工程学院，山东 烟台 264001）

岸基防空兵对高强度攻击目标火力运用*

严建钢，杨士锋，杨大伟

（海军航空工程学院，山东 烟台 264001）

根据航空兵在现代战斗中通常采用的多批次、小间隔连续攻击等高强度攻击的手段，提出了一种岸基防空兵火力运用的“射击强度函数”，应用排队论和优化理论，结合防空兵战术运用原则，求取“函数”中的最优参数，从而得到对此类型攻击目标的火力运用方法，可用于指导岸基防空兵部队的作战与训练。

高强度攻击，随机服务模型，射击强度，火力运用

1 战术原则的数理描述

战术原则是指导岸基防空兵作战的基本依据。往往战术问题的解答不是唯一的，是多元的，与指挥员的战术修养、作战任务有关，这就给建立数学模型带来一定的困难，本文力求反映一般具有指导意义的战术原则，反映敌我双方的作战意图，而且使这些战术原则、作战意图能够融入建立的数学模型之中，指导岸基防空兵的火力运用。

1.1“首战告捷”的数理描述

岸基防空兵作战同其他兵种作战一样，只要歼敌一部，对其整体的影响远远超过其这一部分的存在价值，尤其是在对“多批次、小间隔连续攻击”这种目标作战中显得尤为突出。岸基防空兵利用这一原则成功进行对空防御的例子很多，例如岸基防空兵某部在保卫某铁路桥战斗中，在11'51''内，贯彻“首战告捷”战法，打得敌先头敌机空中开花，前三批24架中被我击落7架，击伤3架，俘敌飞行员4名，迫使第4批架敌机在防区外仓皇投弹而逃。反映在射击上的指导思想就是强调“首战告捷”。用随机系统的排队论模型描述如下：设航空兵或各种导弹按泊松流达到我保卫目标空域，攻击我保卫目标，到达强度为λ，我防区内有若干个“火力单位”（可以是岸基防空旅、营、连等），当航空兵或各种导弹到达时，有两种情况：①遭射击，或者击毁，或者突防；②不遭射击而突防。

“火力单位”对某一批（架）次目标射击的点（齐）射数为m，它是射击时间t的函数，计算公式为：

其中：t0为点（齐）射持续时间；C为点（齐）射间隔。

从以上分析可以看出这个射击点（齐）射数m，显然它应该是一个带参数的值m（t），将这个函数m（t）称作“射击强度”函数，根据战术原则，对此类目标射击时应是一个逐渐衰减的过程，衰减过程与敌方目标攻击的进袭强度λ有关，设为：

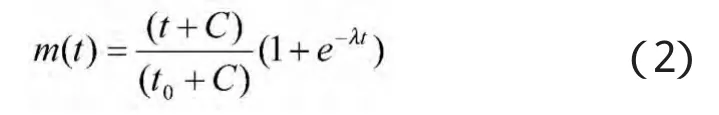
这个模型全面反映了对“多批次、小间隔连续攻击”目标射击的最大射击强度、极限射击强度、强度变化规律。

由此可见，这个模型是markov排队模型中典型的单通道损失制模型［1］，如图1所示。

图1 射击强度函数模型

图中：S0为“火力单位”没有射击；S1为“火力单位“正在射击；μ是武器系统对某个目标的平均射击强度，即单位时间射击目标的批（架次）数，它服从某一分布，具体是什么形式我们并不关心，关心的是反映这种分布的数学期望值的表达式，但不管μ服从什么分布，文献［1］证明了这种系统的模型与极限概率的Markov过程完全相同。

1.2“充分发扬火力”的数理描述

战争或战斗的根本目的是“消灭敌人，保存自己”，只有在大量歼灭敌空袭兵器的基础上，才能有效保障“保卫目标”的安全。因此，模型中必须体现“火力单位”对敌攻击目标击毁概率。其模型为：

（1）“火力单位”一次齐射的击毁概率

“火力单位”一次齐射的击毁概率p应服从指数率，即

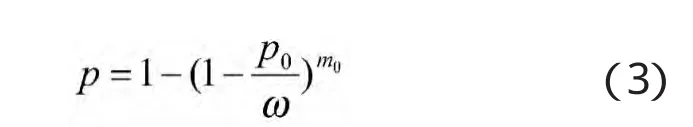
其中：ω为击毁一个目标所需平均必须命中弹数，p0为单发导弹或炮弹的命中概率，m0为“火力单位”一次齐射的数量（导弹或炮弹）。

（2）对一个目标在射击时间t1的击毁概率

对一个目标在射击时间t1内防空武器系统可发射的齐射的次数为

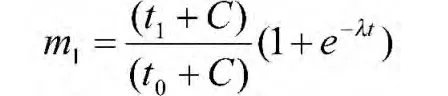
相应的击毁概率p为

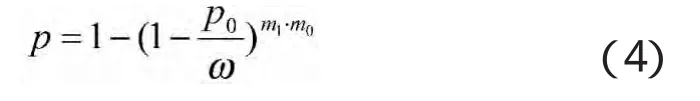
一般研究问题都是在系统稳态下研究，这样能够反映系统的本质特征，所以，根据“射击强度”函数，取其函数的极限值：

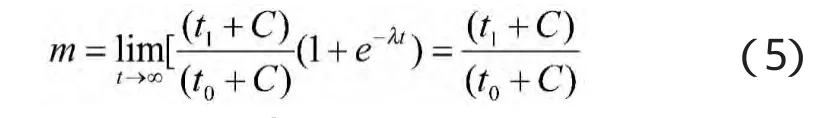
而且令m服从p（X=m0）=1分布，即对每一批（架）次射击的点（齐）射数相同，那么射击的时间t也相同。则对一个目标射击时间t1的击毁概率：

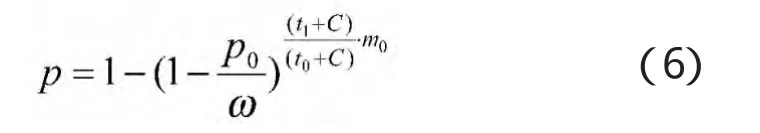
（3）在一定时间T内，对多个目标的击毁概率

假设整个射击时间为一定值T，空袭兵力与兵器总数量为N，由于防空武器系统从捕捉目标到发射完毕需要一定的时间，且对不同的目标存在一定的射击周转时间，所以不可能对所有的空袭兵力与兵器进行射击，能够射击的数量n，可以看作对其中某个目标射击时间t1的函数。

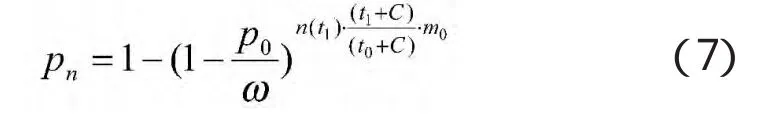
其中：n为航空兵来袭的总批（架）数。

1.3 效益指标“综合性”的数理描述

岸基防空兵历来的效能指标有两个，一是击毁目标的概率，二是“保卫目标”的安全程度。取突破防空网的航空兵突袭兵力与兵器的平均数作为目标函数。

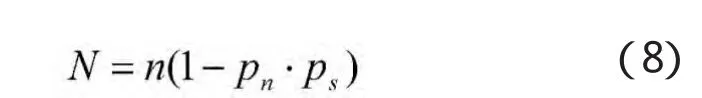
其中：ps为敌空袭兵力与兵器遭到射击的概率；N为敌空袭兵力与兵器突防的平均数。

当防空网对某一批（架）的射击时间t1增加时，p增加，目标遭射击而突防的概率减少，但能够射击的目标数量n（t1）减少，目标不遭射击的那部分突防率就会增大增加；当射击时间t1减小时，p减少，但能够射击的目标数量n（t1）增加，敌机遭到阻击的强度增加，突防率就减小，对“保卫目标”的威胁度就减小。所以，突破防空网的敌机平均数反映了这种“综合性”的指标。

2 数学模型的建立

2.1 效益指标的建立

将整个武器系统等效为一个多“火力单位”对“多批次、小间隔连续攻击”目标射击防空网系统，其效能模型是一个典型Markov过程的单通道损失制排队模型。根据文献［1］，敌机遭到射击概率：

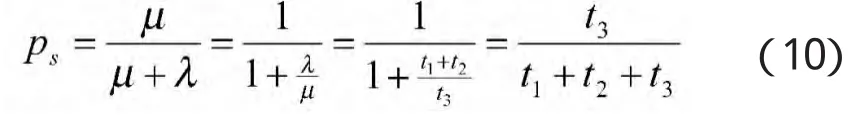
分两种情况讨论：

①当目标来袭的时间问隔t3远大于“火力单位”周转时间与射击时间之和t1+t2时，ps=1；②当t3＜t2时，ps＜1。所以，只讨论第 2种情况，即对“多批次、小间隔连续攻击”目标射击。综合以上讨论，数学模型为：

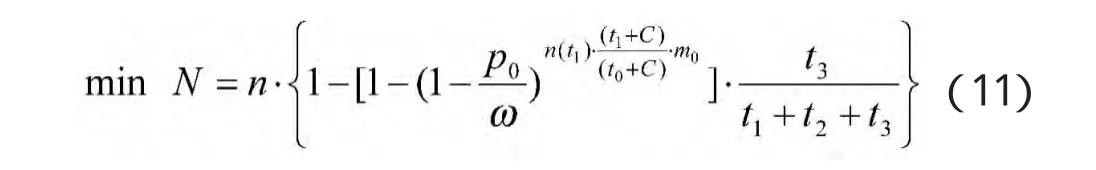
即选择一定的t1（射击时间）使突防的敌机数N为最少。

2.2“射击强度”函数的求取

2.2.1 最优平均点（齐）射数m0的求取

为了反映一般的情况，并且反映防空系统的稳定状态的系统特征，故来袭的目标数n取20批（架）次，按照一定的战术、突袭航路与进袭强度对岸基防空兵所保卫的目标实施攻击，目标的来袭强度分别取 1／20、1／25、1／30、l／35、1／40架／s。根据模拟计算，最优平均射击的齐射数应为2个~3个，从而使敌机突防的架数为最少。

2.2.2 最优射击规律掌握

根据战术原则（1），（2）和文献［2］，设其对某一批（架）次射击的齐射的衰减规律。对第一批（架）次目标应全力打到其航路的投弹前，重点是打前几批（架）次的敌机，根据指数函数的过渡参数规律，当经过3时，式（5）的射击时间趋于稳定值，那么对后续目标应按2个~3个齐射进行射击。

3 结 论

根据式（11）模拟计算可以看出，岸基防空武器系统在稳定状态下的最优发射齐射数是在2个~3个之间，说明对多批次、小间隔连续攻击目标射击不能采取越批（架）次射击，必须按以上介绍的方法控制发射的导弹与炮弹数量，并且适时地转移火力，以求最优的作战效果。

［1］路凤山.排队论及其应用［M］.长沙：湖南科学出版社，1985.

［2］严建钢.空地作战数理战术学［M］.北京：海潮出版社，2000.

Research on FireControl in CoastalAir Defense of High Strength Attack Firepower

YAN Jian-gang，YANGShi-feng，YANGDa-wei
（Naval Aeronautical and Astronautical University，Yantai264001，China）

Based on the continualmulti-batch attack ofmodern air force at short intervals,this paper proposes a shooting intensity function.With the application of lining theory,optimization theory,and tactics principle,the paper works out the optimization parameter of function,thus finding out the best fire control for this attack and guiding the fighting and training of coastal air defense force.

high strength attack firepower，random service model，shooting intensity function，firepower Application

E835；O225

A

1002-0640（2014）02-0055-03

2003-02-18

2013-03-21

国家社会科学基金资助项目（11G J003-074）

严建钢（1958- ），男，山西太原人，博士，教授，博士生导师。研究方向：作战模型及模拟、作战运筹分析及兵力兵器作战运用。