太阳摄动下的地-月系统特性*
张云燕,李 楠,李言俊
(1.西北工业大学航天学院,西安 710072;2.上海卫星工程研究所,上海 200240)
太阳摄动下的地-月系统特性*
张云燕1,李 楠2,李言俊1
(1.西北工业大学航天学院,西安 710072;2.上海卫星工程研究所,上海 200240)
分析了太阳引力摄动下地-月系统的动力学特性。以地-月圆型限制性三体问题为基础,考虑与其非共面的太阳运动,建立了受摄地-月问题的动力学模型;求解此模型的平衡点位置,考察了它们的变化规律及稳定性;构造了非自治系统的类Jacobi积分,从而得到受摄三体系统的零速度面,分析了其连通域随地-月相位的变化情况。计算结果表明,在太阳引力摄动下,地-月系统的平衡点位于无摄三体系统的平动点附近,稳定性也与其附近的平动点保持一致,受摄系统的Hill连通域与地月相位有关,并呈非周期性变化。
受摄地-月系统,平衡点,稳定性,Hill区域
引 言
多体问题的力学特性以及小天体在多体力场中的运动目前正成为深空探测任务中的研究热点。迄今为止,研究最多、应用最广的当数二体问题和三体问题,尤其是三体问题,因其特殊的力学特性,正得到越来越广泛的应用。
三体问题中最常用也是最简单的模型是圆型限制性三体模型,它的研究对象是任何一个相互旋转的两大天体和一个小天体所组成的系统,其中小天体的质量很小,对两大天体的运动几乎没有影响。随着航天任务的不断发展,出现了许多对三体模型的改进和特性研究。文献[1-3]建立了BCP模型,在地-月三体问题中引入了太阳引力的影响,但这个模型假定太阳和地月运行于同一平面内,忽略了黄白交角。文献[4]的模型考虑了第四体的引力摄动,但模型中的三个大天体也位于同一平面内,其模型结构类似于BCP模型。文献[5-6]研究了QBCP模型,它对BCP模型中大天体的运动进行了改进使其自洽,比较复杂,适用范围小。
针对上述问题,本文研究了太阳引力摄动影响下地-月系统的动力学特性。在地-月圆型限制性三体动力学模型中引入了太阳引力,并考虑了黄白交角的存在,建立了太阳摄动下的地-月动力学模型,并对这个模型的各项特性进行了详细研究,考察了太阳引力扰动后系统平衡解的位置变化情况和稳定性,针对时变系统不存在积分常数的问题,构建了此模型的积分不变关系式,在此基础上给出了系统零速度面的变化情况。
1 动力学模型
1.1 圆型限制性三体问题
建立质心旋转坐标系,如图1所示。在此坐标系中,两个大天体m1和m2位于x轴,并绕它们的公共质心O做圆周旋转,旋转平面为xy平面。假定m1>m2,则x轴的方向由m1指向m2,z轴垂直于旋转平面,指向两天体旋转角速度方向,y轴满足右手定则,坐标系原点为O。小天体m3在两大天体引力场中运动,因其质量十分小,因此,它对两大天体的影响可忽略不计。
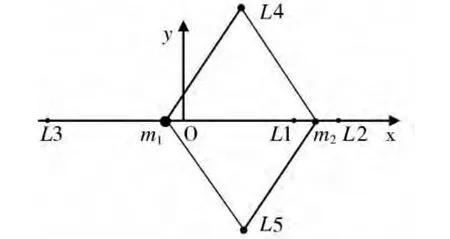
图1 旋转坐标系和平动点
为方便起见,对单位无量纲化,使得两天体间距离、旋转角速度和质量和均为1。令质量比μ为m2/(m1+m2),设 m3的坐标为(x,y,z),则小天体的运动方程可写为[7]
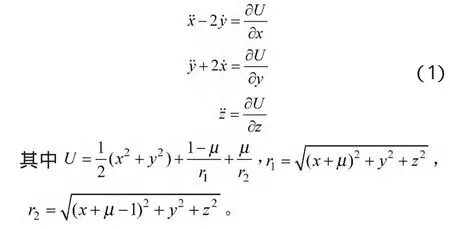
运动方程(1)有5个位于xy平面上的平衡解,或称运动特解,分别定义为L1~L5。其中L1~L3点位于x轴上,称共线平动点;L4和L5分别与两大天体构成等边三角形,称三角平动点。5个平动点的位置见图1。
圆型限制性三体问题存在一个积分常数,称为Jacobi积分:
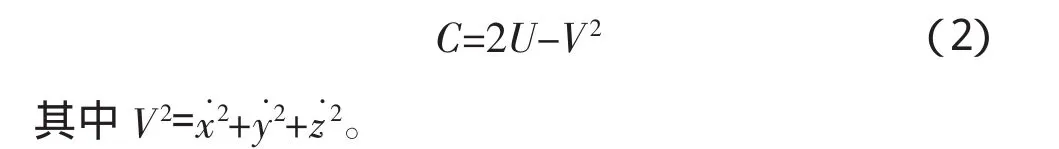
1.2 太阳摄动下的地-月系统
地-月三体系统受到各种摄动力影响,其中量级高的当数太阳引力[8]。考虑太阳引力的影响,建立日-地-月质心惯性坐标系O-XIYIZI,原点O为日-地-月质心,ZI轴垂直于黄道面,其指向由地月质心绕太阳的旋转运动确定。
建立地-月质心坐标系B-X′Y′Z′,其坐标轴指向与O-XIYIZI各坐标轴相同。
令B-xyz为以地-月质心B为原点的质心旋转坐标系,x轴由地球指向月球,z轴为月球绕地球旋转的角速度方向。
图2为各坐标系的示意图。
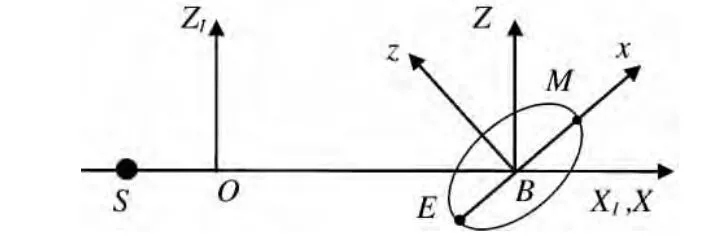
图2 限制性四体问题几何关系及各参考系
采用地月质量和、地月旋转角速度和地月间距离分别作为质量、角速度和长度单位进行无量纲化。假设地球质量为mE,月球质量mM,太阳质量mS,质量比μ=mM/(mM+mE)(下文中μ均指此质量比),太阳旋转速度nS,日-地-月惯性坐标系下小天体运动方程是
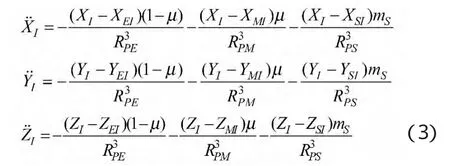
其中下标E代表地球,M代表月球,S代表太阳,下文类似。
设月球运动的升交点赤经为Ω,黄白交角为i,真近点角为f,近地点幅角ω。假定黄道和白道都是圆形,则可令 ω=0。将式(3)经由 B-X′Y′Z 坐标系变换到B-xyz坐标系,得到地-月质心旋转坐标系下小天体的运动方程
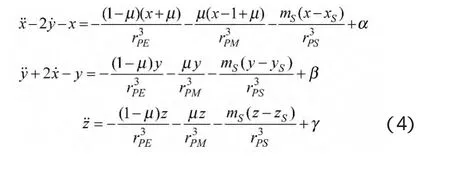
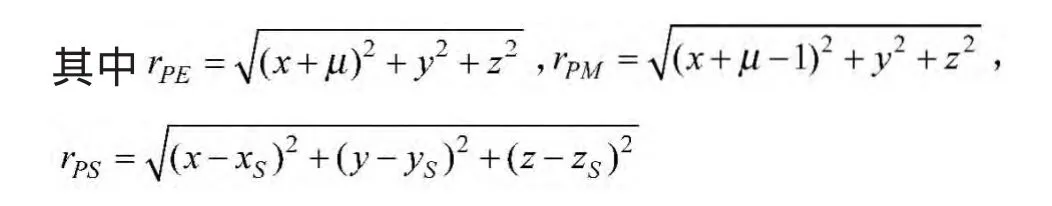
由于黄道和白道都被近似看做圆形,可设f=nt,n=1为地月旋转角速度,令Ω=0,计算得
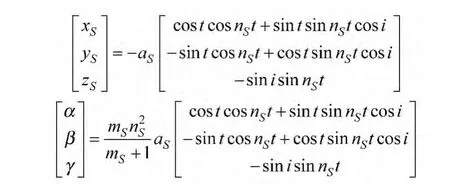
2 平衡解
平动点是圆形限制三体问题的平衡解。大天体多于两个的系统不存在传统意义上的平动点,然而,可以在新的模型下找到新的平衡解。由于太阳对地-月系统的摄动影响,新模型为非自治系统,导致每一时刻平衡解的位置都不一样,因此,在一段时间内可以找到许多平衡解,每个解的存在都是瞬时的。
2.1 L1点和L2点附近的平衡解
对于太阳引力摄动下的地-月系统,在原L1点和L2点附近可以找到新的平衡解,位置如图3和图4所示,黑色方块代表地-月圆型限制性三体问题的平动点。新的平衡解随时间变化的轨迹在三维空间中成准周期轨道,环绕在地-月三体问题的L1和L2点周围,不再保持在xy平面内。
2.2 L3、L4和L5点附近的平衡解
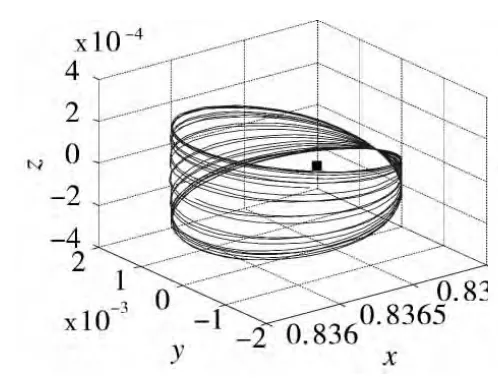
图3 L1点附近平衡解位置轨迹
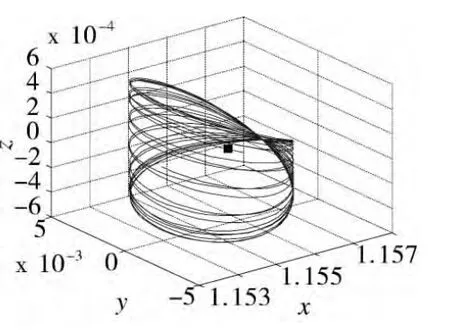
图4 L2点附近平衡解位置轨迹
在L3、L4和L5点附近,也可以找到一系列平衡解,它们的位置也是在原三体问题的平动点附近来回振荡,具体情况见图5~图7。
从计算结果可知,在L1~L5点的附近,不同的时刻,可以找到不同的平衡解。虽然平衡解的位置在不断变化,但始终保持在圆型限制性三体问题的平动点附近。
3 平衡解的稳定性
设平衡解为 L=(x0,y0,z0),令变换 x=x0+ξ,y=y0+η,z=z0+ζ,ξ、η 和ζ为相对于点 L的坐标。将变换代入运动方程(4),得到平衡解附近的线化方程

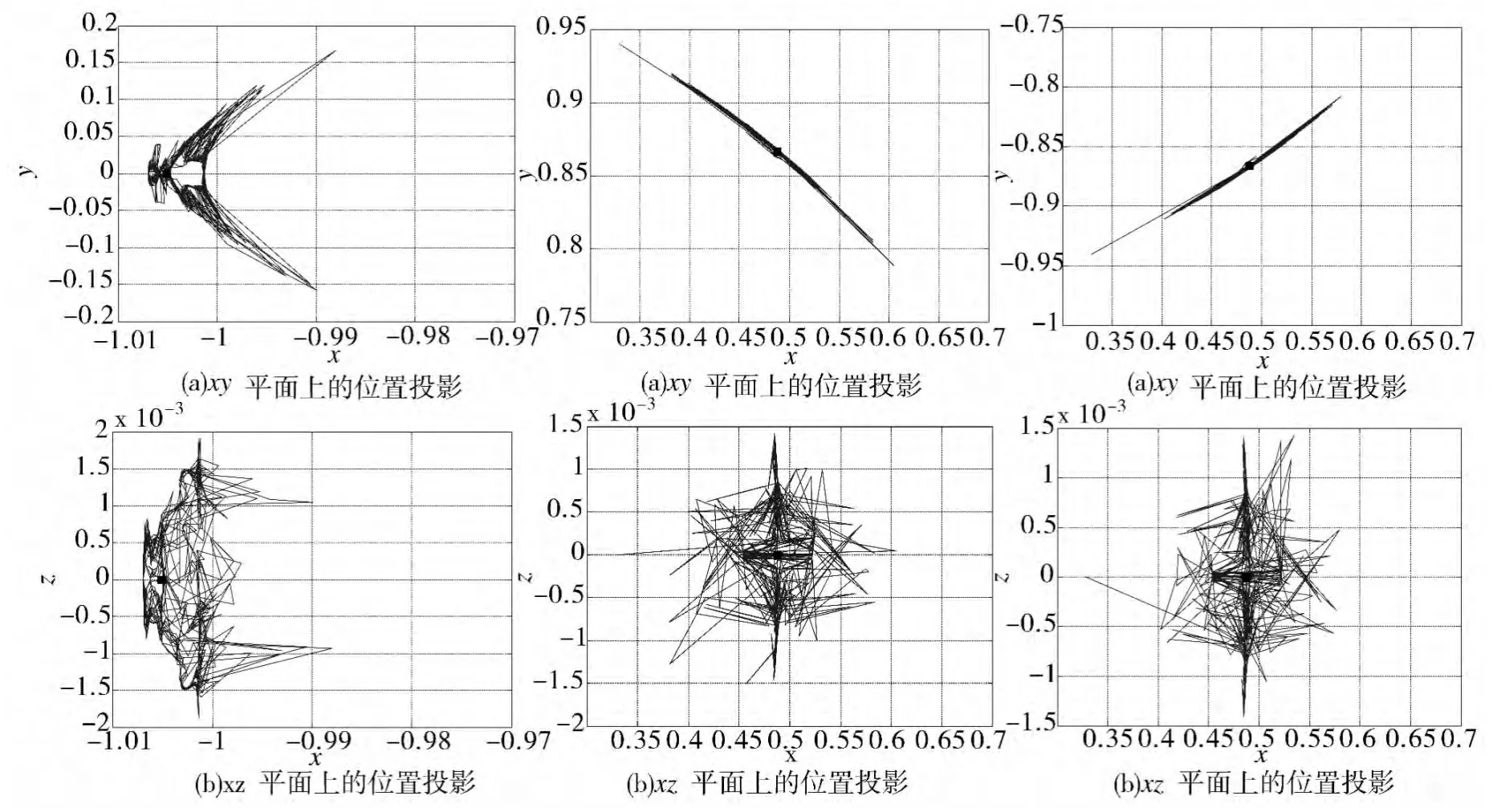
图5 L3点附近平衡解位置变化 图6 L4点附近平衡解位置变化 图7 L5点附近平衡解位置变化
将不同时刻平衡解代入,求取相应的特征值,结果表明,对于L1~L3点附近找到的平衡解,特征值为一对异号实根和两对实部为零的共轭虚根,呈鞍点×中心×中心性态,平衡解不稳定;对于L4和L5附近存在的平衡解,特征根是三对实部为零的共轭虚根,呈中心×中心×中心性态,平衡解在线性意义下临界稳定。已知无摄三体系统的L1~L3点为不稳定的,L4和L5点是临界稳定的。如果将受摄系统在L1~L5点附近求得的新的平衡解视为受摄系统的新的L1~L5点(瞬时的),那么可以得出如下结论:太阳引力摄动不会改变系统平动点的稳定性。
4 Hill区域
加入太阳引力后的非自治系统没有传统意义上的Jacobi积分,但我们可以构造一个积分,它不是常数,但其形式类似Jacobi积分。由运动方程可以得到

C为积分常数,C=2U'0-v02由t0时刻对应的各变量初值确定。
由上式可知,太阳引力摄动下系统的零速度面为C=2U',它是时变的。以t=0和t=π时刻为例,得到如图8所示的零速度面。图中黑点分别代表地球和月球,坐标分别为(-μ,0)和(1-μ,0)。
可见,在太阳引力影响下,小天体运动的可行区域连通性变化和时间t有关,也就是和太阳、地球和月球之间的相位关系有关。两天体之间的可行域并非每时每刻都是连通的,只有相位合适时才能产生地月间的转移轨道。事实上,通过仿真可以发现,对于某一给定Jacobi积分常数C,能够产生地月转移的范围有限,当Ω初值为0时,在第一个地月运动周期内,地月转移窗口大约在地月相位为137°~252°的范围内(1 698 图8 零速度面 本文建立了日地月非共面的太阳引力摄动下的地-月系统动力学模型,并对其各项特性进行了详细分析。计算结果表明,考虑黄白交角,在太阳引力作用下,在每一个时刻,地-月系统存在与平动点位置不同的平衡解,这些平衡解不会偏离平动点位置太远,稳定性也与平动点保持一致。此外,通过构造这个受摄时变系统的类似Jacobi积分形式的积分关系式,得到了受摄地-月系统的零速度面。经过分析得知,太阳引力摄动使原地-月系统的零速度面变为非周期时变的,Hill连通域随地-月相位变化而发生相应的改变。 另外,将本文的动力学模型参数作相应调整,还可应用于其他天体系统。 [1]Yagasaki K.Sun-Perturbed Earth-to-Moon Transfers with Low Energy and Moderate Flight time[J].CelestialMechanicsand DynamicalAstronomy,2004,90(11):197-212. [2]Yagasaki K.Computation of Low Energy Earth-to-Moon Transfers with Moderate Flight time[J].Physica D,2004,197(10):313-331. [3]Simo C,GomezG,Jorba A,etal.The BicircularModelNear the Triangular Llibration Pointsof the RTBP[C]//Roy A E,Steves BA.From Newton to Chaos.New York:Plenum Press,1995. [4]Guzman JJ.Spacecraft Trajectory Design in the Contextofa CoherentRestricted Four-body Problem[D].Indiana:Purdue University,2001. [5]Andreu M A.TheQuasi-Bicircular Problem[D].Spain:Uni-Versitatde Barcelona,1998. [6]Andreu M A.Dynamics in the CenterManifold Around L2 in the Quasi-Bicircular Problem[J].Celestial Mechanics and DynamicalAstronomy,2002,84(10):105-133. [7]Howell KC.Three-Dimensional,Periodic,‘halo’orbits[J].CelestialMechanics,1984,32(1):53-71. [8]刘 林,王 歆.月球卫星轨道力学综述[J].天文学进展,2003,21(4):281-288. Research on Propertiesof Sun-Perturbed Earth-M oon System ZHANGYun-yan1,LINan2,LIYan-jun1 The dynamical properties of Sun-perturbed Earth-Moon system are analyzed.Based on the circular restricted three body problem,the perturbed Earth-Moon dynamicalmodel is established,considering the non-coplanarmovement of the Sun.The equilibriums of thismodel are calculated,and their positions and stabilities are investigated.An integral similar with Jacobi energy is constructed to obtain the zero curve of this perturbed three body system,then it is capable to analyze the Hill region of this system.The results show that under the gravitational influence of the Sun,the equilibriums of the Earth-Moon system tend to be located near the libration points of the non-perturbed system,and also keep the same stability.The Hill region of the perturbed system will change non-periodically with the lunar phase. perturbed Earth-Moon system,equilibrium,stability,Hill region V142.4 A 1002-0640(2014)02-0025-04 2013-01-28 2013-03-09 国家自然科学基金(61174204);航天支撑基金资助项目(NAXW 0006) 张云燕(1982- ),女,山东招远人,博士生。研究方向:深空探测,轨道设计。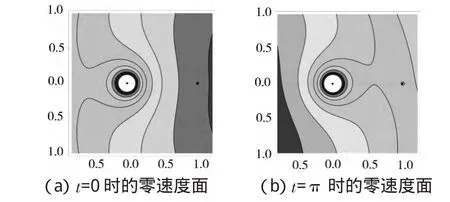
5 结论
(1.School of Astronautics,Northwestern Polytechincal University,Xi’an 710072,China;2.Shanghai Institute of Satellite Engineering,Shanghai200240,China)

