基于模糊聚类的雷达信号分选*

尹 亮，潘继飞，姜秋喜

（电子工程学院安徽省电子制约技术重点实验室，合肥 230037）

基于模糊聚类的雷达信号分选*

尹 亮，潘继飞，姜秋喜

（电子工程学院安徽省电子制约技术重点实验室，合肥 230037）

为克服传统信号分选算法的局限性，采用了基于模糊聚类分析的雷达脉冲信号分选方法。首先介绍了模糊聚类的基本原理和具体步骤，利用熵权法对不同雷达信号特征参数增加了加权系数，其次建立了有效性评价模型来确定最佳聚类，并进行了信号分选仿真实验。利用该方法进行模糊聚类时无需设置阈值，仿真结果证明分选方法的正确性，验证了此方法的有效性和可行性。该方法能够处理多个雷达脉冲信号，是一种解决多脉冲信号分选问题的新途径。

模糊聚类，雷达信号分选，熵权，有效性评价模型

引 言

随着电子侦察设备的广泛使用，雷达信号的密度越来越大，信号越来越复杂。侦察接收系统首要面临的问题是对密集交迭的雷达信号进行自动分选。因此，雷达信号分选是电子侦察信号处理中的关键技术之一［1］。近些年来常用的聚类方法有:基于神经网络的聚类方法［2］、STING算法［3］、CLIQUE算法［4］以及CURE算法［5］。虽然这些算法在理论上可以实现信号的分选，但它们都有一个致命的缺点:确定聚类中心和聚类半径［6］。在实际雷达信号分选中做到这点是非常困难的。

模糊聚类分选雷达信号是采用模糊数学方法，根据信号的各种参数，按某些预定特征参数进行分选。模糊聚类的优点在于它能适应那些分离性不是很好的雷达信号，并且无需确定聚类中心和聚类半径。模糊聚类法是根据信号之间的模糊性建立起样本之间的类别差异，能更客观反映雷达信号特点。传统的模糊聚类需要人工设置阈值进行聚类，阈值的不同对聚类的结果有很多的影响。通过熵值确定各特征参数的加权系数和建立有效性评价模型，无需人工设定阈值即可进行聚类，提高了聚类的可信性和实时性。

1 模糊聚类算法原理

1.1 模糊聚类算法原理

现代接收机一般通过测量信号的脉冲描述字PDW对雷达信号进行聚类，PDW一般包括信号载频（RF）、脉冲宽度（PW）、调制样式（PM）、脉冲幅度（PA）、到达方向（DOA）和脉冲重复间隔（PRI）等特征参数。对于n个脉冲信号，假设每个信号包含m维特征参数，则有样本数据 PDW=（PDW1，PDW2，…，PDWn）T，其中PDWi=（RFi，PWi，PMi，…，PRIi）。则信号样本PDW可以表示为

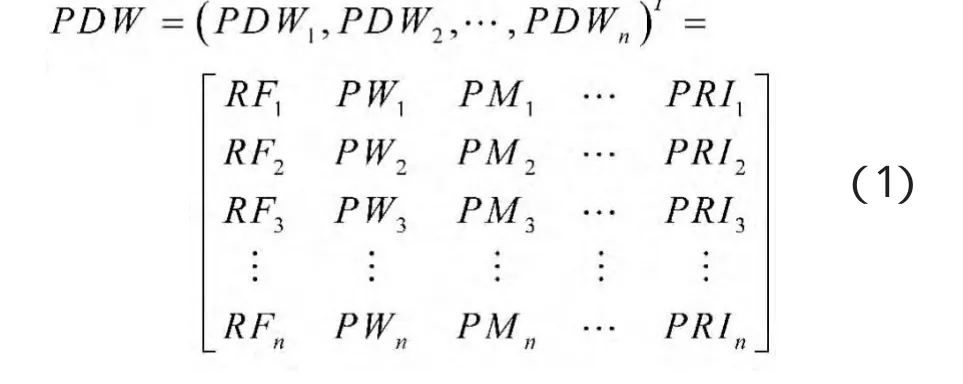
对这些样本数据建立模糊相似关系，即用数rij∈［0,1］来衡量物件PDWi与PDWj对应元素的相关程度，从而得到模糊相似矩阵R=（rij）n×n，rij=rij且rij=1。其中rij的确定有以下几种常用方法，有数积法、夹角余弦法、相关系数法、最大最小法、算术平均最小法、几何平均最小法、绝对值指数法、绝对值减数法以及海明距离法等。

1.2 模糊聚类的具体步骤

1.2.1 数据标准化处理

实际应用中，所得原始PDW往往比较复杂，为排除原始PDW中变量之间的不同度量对聚类的影响，需要对原始PDW进行必要的处理，使其分布在相同的区间［0，1］内，以相同的量级参与聚类。

1.2.2 熵值法确定加权系数

计算样本数据PDW的相似统计量，常用的计算方法有多种，在此选用海明距离法。由于不同雷达信号的特征参数在聚类分选中的作用不同，因此，不同特征参数需不同的加权系数，即：

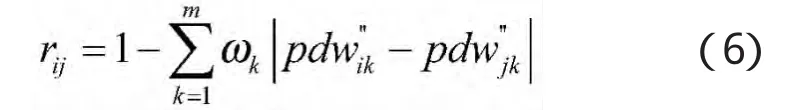
其中ωk是第k维特征参数的加权系数。ωk的确定方法有层次分析法、专家经验法以及熵值法等。在信号分选中，熵值是对某项参数无序程度的度量，某项参数的变化度越小，其熵值越大，对应加权系数就越小。反之，某项参数变化度越大，其熵值越小，对应加权系数就越大。相较于层次分析法和专家经验法，熵值法确定加权系数，不需加入人为因素干扰。因此，熵值法得到的加权系数更加客观，更加有效。熵值法确定加权系数的步骤如下：

第1步：计算第j维参数下的第i个数据的权重Qij：

对于给定的信号参数，某项参数变化度越小，则对应的加权系数越小，如果某项参数均相等则该项参数对综合分选没有作用，加权系数即为0。反之，某项参数变化度越大，则对应的加权系数越大。

据此，可建立PDW的模糊相似性关系R=（rij）n×n，0≤rij≤1，i，j=1，2，…，n，rij表示第 i个样本与第 j个样本的相似度。

1.2.3 进行模糊聚类

用上述方法建立起来的模糊相似关系矩阵R，满足自反性rij=1、对称性rij=rij，但不满足传递性，该矩阵还不具有模糊等价关系，必须对其进行改造。利用传递闭包法从模糊相似矩阵R出发，依次求rk）j，。其中，∨为两数取大运算（逻辑加），∧为两数取小运算（逻辑乘）。

当满足Rk○Rk=Rk时，表明Rk具有传递性，Rk就是所求的模糊等价矩阵:

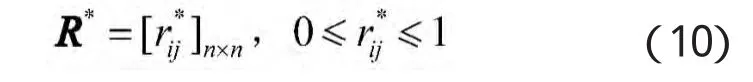
2 基于有效性函数的确定最佳聚类算法

由于模糊聚类过程没有量化的标准来定义哪种聚类结果是有效的，阈值的设定是依靠经验确定的。然而，阈值的变化对聚类的结果和性能影响较大，因此，根据经验选取的阈值无法保证聚类结果的准确性。聚类的目标是使样本达到类内紧密，类间远离。本文将经过标准化处理的样本数据PDW''作为研究对象，从耦合度和分离度出发，建立聚类有效性评价模型，对选择的阈值给出有效性评价，从而确定最佳聚类结果［2］。

耦合度定义为:分离度反映了不同类之间的差异性。

分别将紧致度和分离度除以相应的权值，以降低类数对有效性评价的影响，然后用分离度和紧致度进行比较，以获取最大的评价值，建立的聚类有效性评价模型为:

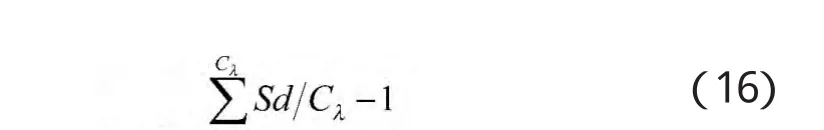
所有样本各自成类或全部并成一类，在实际应用中没有多大意义，文献［8］在理论上证明了经验规则的合理性，因此。比较不同Cλ时所得到的F值，最大F值所对应聚类结果即为最佳聚类结果，所对应阈值λ即为最佳阈值。

3 实验结果及分析

为验证上述方法的有效性，利用MATLAB仿真产生4部雷达的PDW（包括脉幅、脉宽、脉冲重复周期3个参数），每部雷达产生30个PDW，4部雷达的参数设置如表1所示，每次仿真产生的PDW是不同的。实际测量中PDW总存在个别错误数据，因此，假设雷达1、2、3、4中各有一个错误的PDW。为方便观测聚类结果，依次将所产生的4组PDW放在一个矩阵中，即1-30为雷达1，31-60为雷达2，61-90为雷达3，91-120为雷达4。由前文分析可知，聚类数Cλ应满足。利用上述方法进行10次模糊聚类，其中1个仿真结果如表1所示。

表1 4部雷达特征参数

用熵值法确定的雷达特征参数加权系数为ω=（0.34,0.37,0.29）。图1为聚类数与F值变化关系图，横坐标为聚类数Cλ，纵坐标为对应的F值，可看出，聚类数为8时对应的F值最大。相应的仿真聚类结果为：以上数据可以分为8类。

第1类为：1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29；第2类为：30；第 3类为：31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59；第 4类为：60；第5类为：61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89；第 6类为：90；第7类为：91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119；第8类为：120。

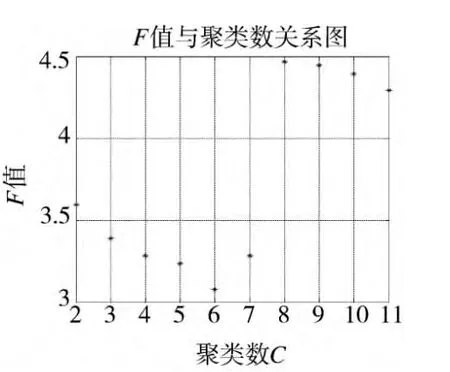
图1 F值与聚类数Cλ关系图

可以看出，第2、4、6、8类只含有1个PDW，即为错误数据，在实际聚类中也没有实际意义，可将其滤去。因此，最后的聚类结果只有4类，与仿真产生的PDW一致。利用该方法仿真10次，虽然每次产生的PDW有所不同，但每次的聚类结果是一致的，证明了该聚类方法的可行性和有效性。

5 结束语

上述分析和仿真表明模糊聚类法能够利用雷达信号的特征参数有效地完成复杂雷达信号分选任务。依据熵值法确定雷达特征参数的加权系数和有效性评价模型，可以直接得到最佳聚类结果，克服了以往模糊聚类需要人为设置阈值的缺点，是雷达信号分选的新方法。

［1］罗景青.雷达对抗原理［M］.北京：解放军出版社，2003.

［2］Kohonen T.The Self-Organizing Map［J］.IEEEDecision，1990，78（9）:1464-1480.

［3］ WangW，Yang J，Muntz R.STING:A Statistical Information Grid Approach to SpatialDataMining［C］//Proc.of the 23rd InternationalConferenceon very Large Data Bases，1997.

［4］ Agrawal R，Gehrke J，Gunopulcs D.Automatic Subspace Clustering of High Dimensional Data for Data Mining Application［C］//Proc.of ACM SIGMOD Intconfon Managementon Data，Seattle，WA，1998.

［5］Guha S，Rastogi R，Shim K.Cure:An Efficient Clustering Algorithm for Large Database ［C］ //Proc.of ACM-SIGMOND Int，Conf，Management on Data，Seattle，Washington，1998.

［6］刘旭波，司锡才.基于改进的模糊聚类的雷达信号分选［J］.弹箭与制导学报，2009，29（5）:278-282.

［7］赵德滨，宋利利，闫纪红.基于模糊聚类分选的特征识别方法及其应用［J］.计算机集成制造系统，2009，15（12）:2417-2423.

［8］李士勇.工程模糊数学及应用［M］.哈尔滨:哈尔滨工业大学出版社，2004.

［9］杨善林，李永森，胡笑旋，等.K-means算法中的k值优化问题研究［J］.系统工程理论与实践，2006，26（2）:97-101.

A Study on Sorting of Radar-Signals Based on Fuzzy Clustering

YIN Liang，PAN Ji-fei，JIANGQiu-xi
（Electronic Engineering Institute，Key Laboratory of Electronic Restriction Anhui Province，Hefei230037，China）

In order to overcome the limitation of traditional radar-signals sorting algorithm，a radar pulse signal sortingmethod based on fuzzy clustering is presented.Firstly，the basic principle and steps of fuzzy clustering are introduced.The weights of parameters are determined according to entropy.The model of effective evaluation is built to determine the best sorting.Finally，the experiment is simulated.The simulation shows that themethod is effective and feasible.Themethod fits for processing a large amount of data.It provides a new way to solve sorting problems of dense and complicated pulse signals.

fuzzy cluster，radar-signalsorting，entropyweight，modelofeffectiveevaluation

TN95

A

1002-0640（2014）02-0052-03

2013-02-18

2013-03-22

“：十二五”国防预研基金资助项目（41101020207）

尹 亮：（1987- ），男，安徽铜陵人，硕士研究生。研究方向：电子对抗装备新技术。