Interpolation by Bivariate Polynomials Based on Multivariate F-truncated Powers

(General Courses Department,Academy of Military Transportation,Tianjin,300160)

Interpolation by Bivariate Polynomials Based on Multivariate F-truncated Powers

YUAN XUE-MEI

(General Courses Department,Academy of Military Transportation,Tianjin,300160)

Communicated by Ma Fu-ming

The solvability of the interpolation by bivariate polynomials based on multivariate F-truncated powers is considered in this short note.It uni fi es the pointwise Lagrange interpolation by bivariate polynomials and the interpolation by bivariate polynomials based on linear integrals over segments in some sense.

multivariate F-truncated power,point-wise Lagrange interpolation, solvability of an interpolation problem

1 Introduction

Suppose that M is an s×n real matrix with rank(M)=s and f(x1,···,xn)is an n-variables real function de fi ned on

The multivariate F-truncated power Tf(·|M)associated with M and f is de fi ned as in[1]:

where D(Rs)is the space of test functions onRs,i.e.,the space of all compactly supported and in fi nitely di ff erentiable functions onRs.

Based on(1.1),one can conclude that(see[1])

whereµis the Lebesgue measure on the(n−s)-dimensional affine variety H that contains

Based on(1.2),one can see that Tf(x|M)is linear with respect to f,that is,

and

Moreover,if f≡1,then

is reduced to the classical multivariate truncated power.

We next turn to an interpolation problem.We useto denote the n-variables polynomial space of total degrees no larger than l.Given a set of pairs{(x(i),M(i))}where M(i)are s×n real matrices,x(i)∈Rs,and N=We say that it is poised inif for all⊂Rthere exists a unique P∈such that

The interpolation problem(1.3)is called the interpolation by multivariate polynomials based on multivariate F-truncated powers.If{(x(i),M(i))}is poised inthen(1.3)is called to be solvable.It is easy to see that{(x(i),M(i))}is poised inif and only if

which implies P≡0.

In this short note,we only consider the solvability of(1.3)for the cases n=2 and s=1,2.Sufficient and necessary conditions are obtained to guarantee the set of pairs {(x(i),M(i))}to be poised.Referring to the point-wise Lagrange interpolation by bivariate polynomials(see[2–3])and the interpolation by bivariate polynomials based on linear integrals over segments(see[4–6]),for the case that n=2 and s=2,(1.3)is a point-wise Lagrange interpolation by bivariate polynomials and for the case that n=2 and s=1 is an interpolation by bivariate polynomials based on linear integrals.Therefore we can say that we unify the point-wise Lagrange interpolation and the interpolation based on linear integrals to the interpolation based on multivariate F-truncated powers.Our main results are stated as follows.

Theorem 1.1Suppose thatn=2ands=2.The set of pairs{(x(i),M(i))}is poisedinif and only if

and{(M(i))−1(x(i))is poised for the point-wise Lagrange interpolation inwhere

andmij(j=1,2)are the column vectors ofM(i).

Theorem 1.2Suppose thatn=2ands=1.The set of pairs{(x(i),M(i))}is poisedinif and only if

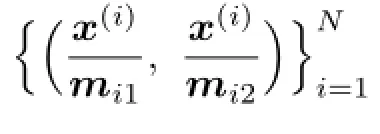
l.

For convenience we state two useful lemmas as follows.

Lemma 1.1[1]Iff(x1,x2)=thenTf(x|M)=k1!k2!T(x|M(k1,k2)),wherem1∈R,m2∈R,andM=(m1,m2).

Lemma 1.2[7]LetM=(m1,m2,···,mn)be a1×n(n＞1)real matrix such that the origin is not contained in

2 Proofs of the Theorems

Proof of Theorem 1.1By(1.2),x(i)∈cone(M(i))(i=1,2,···,N)are necessary to guarantee{(x(i),M(i))}to be poised,and then

The interpolation becomes the point-wise Lagrange interpolation.

Proof of Theorem 1.2By(1.2),x(i)∈cone(M(i))(i=1,2,···,N)are necessary to guarantee{(x(i),M(i))}to be poised,and then

satis fi es

where the second equation is got by Lemma 1.1 and the third equation by Lemma 1.2.Since

under the conditions that

we have

which implies

[1]Xu Z.Multivariate F-splines and fractional box splines.J.Fourier Anal.Appl.,2009,15:723–738.

[2]Hakopian H.Multivariate divided di ff erences and multivarite interpolation of Lagrange and Hermite type.J.Approx.Theory,1982,34:286–305.

[3]Liang X.Multivariate Polynomial Interpolation and Approximation.Master’s Thesis.Changchun:Jilin University,1965.

[4]Bojanov B,Georgieva I.Interpolation by bivariate polynomials based on Radon projections. Studia Math.,2004,162:141–160.

[5]Cavaretta A,Micchelli C,Sharma A.Multivariate interpolation and the Radon transform,Part I.Math.Z.,1980,174:263–279.

[6]Cavaretta A,Micchelli C,Sharma A.Multivariate Interpolation and the Radon Transform, Part II.in:DeVore R,Scherer K.Quantitive Approximation.New York:Academic Press,1980: 49–62.

[7]Micchelli C.On a Numerically Efficient Method for Computing Multivariate B-splines.in: Schempp W,Zeller K.Multivariate Approximation Theory.Basel:Birkh¨auser,1979:211–248.

tion:41A05,41A10,41A15,65D05

A

1674-5647(2014)04-0379-04

10.13447/j.1674-5647.2014.04.11

Received date:July 4,2013.

Foundation item:The NSF(10401021)of China.

E-mail address:yuanxuemei 8013@163.com(Yuan X M).