Jordan Left Derivations of Generalized Matrix Algebras

Jordan Left Derivations of Generalized Matrix Algebras

LI CHEN-FANG AND LI YAN-BO*

(School of Mathematics and Statistics,Northeastern University at Qinhuangdao,Qinhuangdao, Hebei,066004)

Communicated by Du Xian-kun

In this paper,it is proved that under certain conditions,each Jordan left derivation on a generalized matrix algebra is zero and each generalized Jordan left derivation is a generalized left derivation.

generalized Jordan left derivation,Jordan left derivation,generalized matrix algebra,generalized left derivation

1 Introduction

Let us begin with the de fi nition of generalized matrix algebras given by a Morita context.Let R be a commutative ring with identity.A Morita context consists of two R-algebras A and B,two bimodulesAMBandBNA,and two bimodule homomorphisms called the pairings ΦMN:M ⊗BN −→ A and ΨNM:N⊗AM −→ B satisfying the following commutative diagrams:

Let us write this Morita context as(A,B,AMB,BNA,ΦMN,ΨNM).If(A,B,AMB,BNA, ΦMN,ΨNM)is a Morita context,then the set

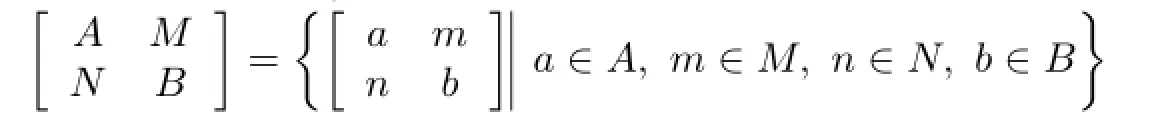
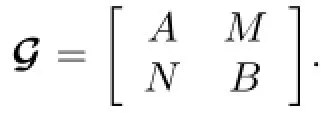
Let A be a unital algebra over R,and M be a left A-module.Recall that an R-linear map f from A into M is called a left derivation if f(ab)=af(b)+bf(a)and called a generalized left derivation if there exists another R-linear map d such that f(ab)=af(b)+bd(a). Further,an R-linear map J from A into M is called a Jordan left derivation if J(a2)= 2aJ(a)for all a∈A,and called a generalized Jordan left derivation if J(a2)=aJ(a)+ad(a), where d is a Jordan left derivation.Let M be a A-A-bimodule.An R-linear map f from A into M is called a derivation if f(ab)=f(a)b+af(b)for all a,b∈A,a generalized derivation if f(ab)=f(a)b+ad(b),where d is a derivation from A to M and a Jordan derivation if J(a2)=J(a)a+aJ(a)for all a∈A.

Note that the concept of Jordan left derivation were introduced by Breˇsar and Vukman[6]. Han and Wei[7]studied generalized Jordan left derivations of semiprime algebras.They proved that any generalized Jordan left derivation on a semiprime algebra of characteristic not 2 is a generalized left derivation and is also a generalized derivation.The aim of this note is to study Jordan left derivations and generalized Jordan left derivations of generalized matrix algebras.We prove that under certain conditions,each Jordan left derivation onis zero.As a by-product,we get that under certain conditions,each generalized Jordan left derivation ofis a generalized left derivation.

2 Jordan Left Derivations of Generalized Matrix Algebras

From now on,we always assume that all algebras and modules considered in this note are 2-torsion free.Let us fi rst describe the general form of Jordan left derivations on generalized matrix algebras.

Lemma 2.1An additive mapΘfromGinto itself is a Jordan left derivation if and only if it is of the for

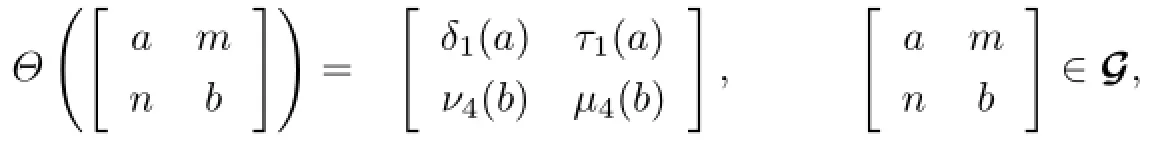
where

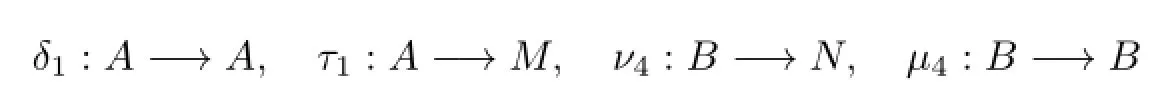
are allR-linear maps satisfying the following conditions:

(1)δ1is a Jordan left derivation onA,δ1(mn)=0andnδ1(a)=0;

(2)τ1is a Jordan left derivation fromAintoM,τ1(mn)=0andnτ1(a)=0;

(3)ν4is a Jordan left derivation fromBintoN,ν4(nm)=0andmν4(b)=0;

(4)µ4is a Jordan left derivation onB,µ4(nm)=0andmµ4(b)=0.

for all where δ1,δ2,δ3,δ4are R-linear maps from A,M,N,B to A,respectively;τ1,τ2,τ3,τ4are R-linear maps from A,M,N,B to M,respectively;ν1,ν2,ν3,ν4are R-linear maps from A,M,N,B to N,respectively;µ1,µ2,µ3,µ4are R-linear maps from A,M,N,B to B,respectively.

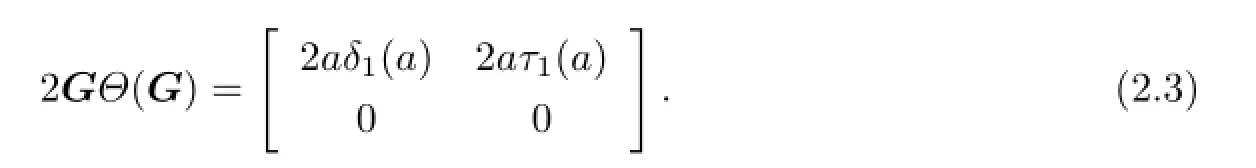
and into(2.1)we have

By(2.2)and(2.3)we know that δ1and τ1are both Jordan left derivations and

and

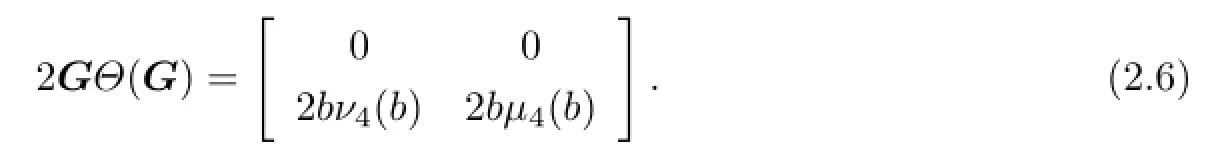
Combining(2.5)with(2.6)yields that ν4andµ4are Jordan left derivations and

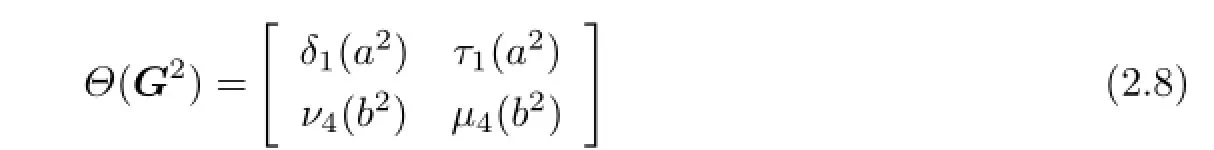
and

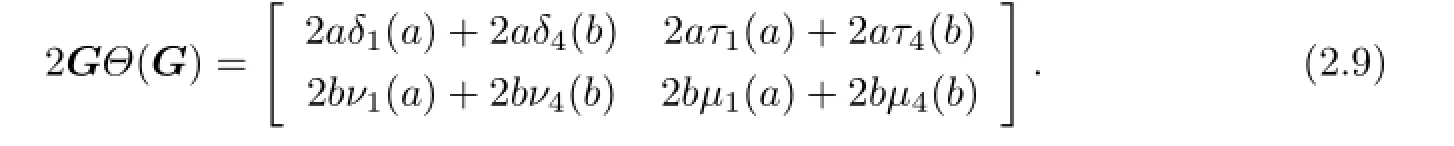
By(2.8)and(2.9),we arrive at

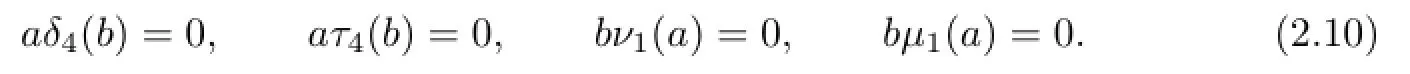
Substituting a=1 and b=1 into(2.10),respectively,give that

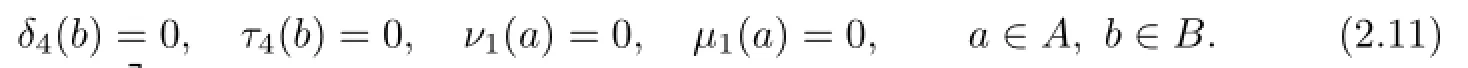
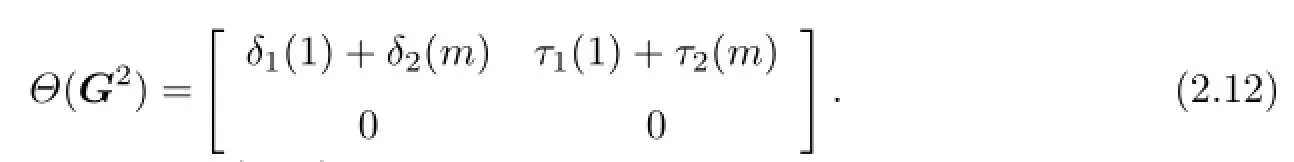
On the other hand,according to(2.11),we have

Combining(2.12)with(2.13)leads to

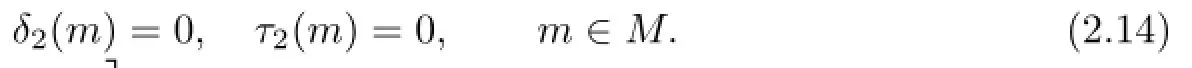
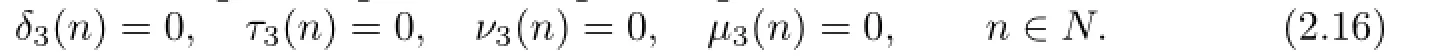
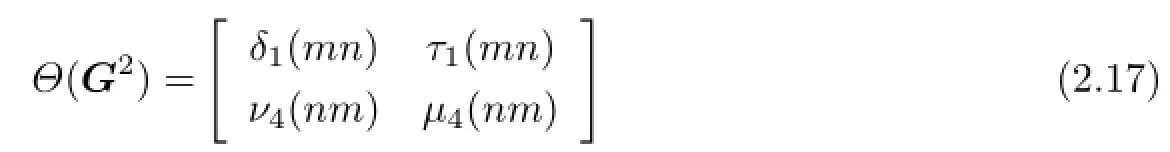
and

The equalities(2.17)and(2.18)jointly imply that

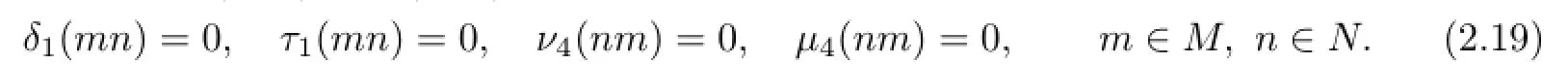
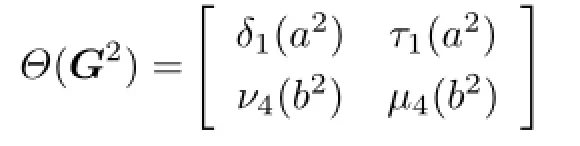
and

The above two equalities jointly imply that

We complete the proof.

bimodule.Combining this de fi nition with Lemma 2.1,we obtain the following result.be a generalized matrix algebra with the pairingsΦMNandΨNMbeing nondegenerate.Then anR-linear mapfofis a Jordan left derivation if and only iff=0.

Let us consider generalized Jordan left derivations of a generalized matrix algebra G.We need the following lemma.

Lemma 2.2Letfbe anR-linear map ofG.Thenfis a generalized left derivation if and only if it is of the formf(a)=af(1)+d(a)for alla∈G,wheredis a left derivation ofG.

Proof.“⇒”.Let f be a generalized left derivation of G.Then there exists another R-linear map d such that

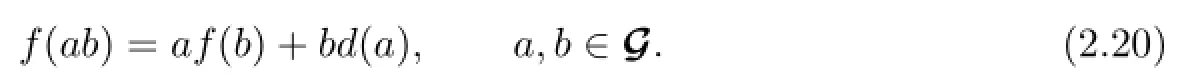
Taking b=1 into(2.20)gives that

and consequently

On the other hand,we have from(2.20)that

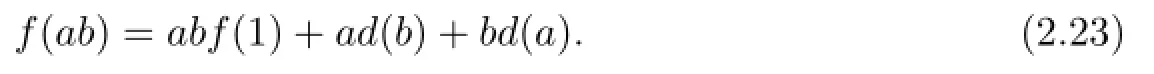
Combining(2.22)with(2.23)yields that d is a left derivation.

“⇐”.Let f be an R-linear map of the form(2.21).Then for arbitrary a,b∈G, substituting bf(1)=f(b)−d(b)into(2.22)implies that f is a generalized left derivation of G.

Corollary 2.1If the pairingsΦMNandΨNMare nondegenerate,then each generalized Jordan left derivation ofGis a generalized left derivation.

Proof.Let J be a generalized Jordan left derivation on G.Then

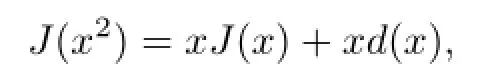
where d is a Jordan left derivation on G.Since the pairings ΦMNand ΨNMare nondegenerate,we have from Theorem 2.1 that d=0.This forces

Setting x=a+b in(2.24)yields that

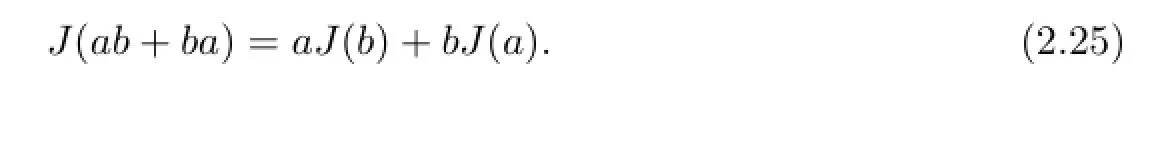
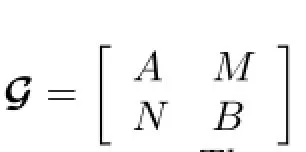
Putting b=1 into(2.25),we obtain that

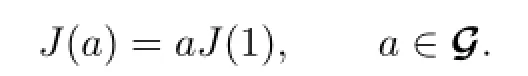
Hence J is a generalized left derivation by Lemma 2.2.This is the end of the proof.

Note that the condition in Theorem 2.1 is not necessary.We illustrate an example from generalized one-point extension algebras here.For details,we refer the readers to[8–9].Example 2.1LetΓbe a quiver as follows

and letΛ=KΓ.The generalized one-point extension algebra E(Λ)has a basis

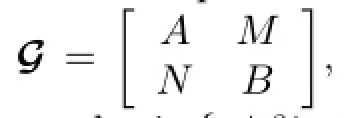
It follows from the de fi nition of generalized one-point extension algebras that the pairings ΦMNand ΨNMare both zeros.Then clearly,both ΦMNand ΨNMare not nondegenerate. By direct computations,we obtain that each Jordan left derivation of E(Λ)is zero.We omit the details here.

[1]Li Y B,Wei F.Semi-centralizing maps of genralized matrix algebras.Linear Algebra Appl., 2012,436:1122–1153.

[2]Li Y B,Wei F.Jordan derivations and anti-derivations of genralized matrix algebras.Oper. Matrices,2013,7:399–415.

[3]Li Y B,Wei F.K-commuting mapings on genralized matrix algebras.arXiv:1111.6316[math. RA].Submitted on 27 Nov.2011.

[4]Li Y B,Xiao Z K.Additivity of maps on generalized matrix algebras.Elect.J.Linear Algebra, 2011,22:743–757.

[5]Xiao Z K,Wei F.Commuting mappings of generalized matrix algebras.Linear Algebra Appl., 2010,433:2178–2197.

[6]Breˇsar M,Vukman J.On left derivations and related mappings.Proc.Amer.Math.Soc.,1990,110:7–16.

[7]Han D,Wei F.Generalized Jordan left derivations on semiprime algebras.Monatsh.Math., 2010,161:77–83.

[8]Li Y B,Wei F.Lie derivations of dual extensions.arXiv:1303.0831[math.RA].Submitted on 2 March 2013.

[9]Li Y B,Wei F.Jordan derivations of some extension algebras.arXiv:1303.0372[math.RA]. Submitted on 2 March 2013.

tion:15A78,16W25,47L35

A

1674-5647(2014)04-0301-06

10.13447/j.1674-5647.2014.04.03

Received date:Jan.30,2013.

Foundation item:Fundamental Research Funds(N110423007)for the Central Universities.

*Corresponding author.

E-mail address:yingshulcf2010@163.com(Li C F),liyanbo707@163.com(Li Y B).